Angenommen, der beschriebene Test wird auf der Grundlage einer Stichprobe von nur 100 Touristen durchgeführt. In diesem Fall wird die Nullhypothese abgelehnt, wenn sich unter diesen mehr als 20 Radausflügler befinden. Damit die Wahrscheinlichkeit für den Fehler zweiter Art höchstens 30 % beträgt, muss der tatsächliche Anteil der Radausflügler unter allen Touristen mindestens einen bestimmten Wert haben. Ermitteln Sie diesen Wert auf ganze Prozent genau und beschreiben Sie die Bedeutung des Fehlers zweiter Art im Sachzusammenhang.
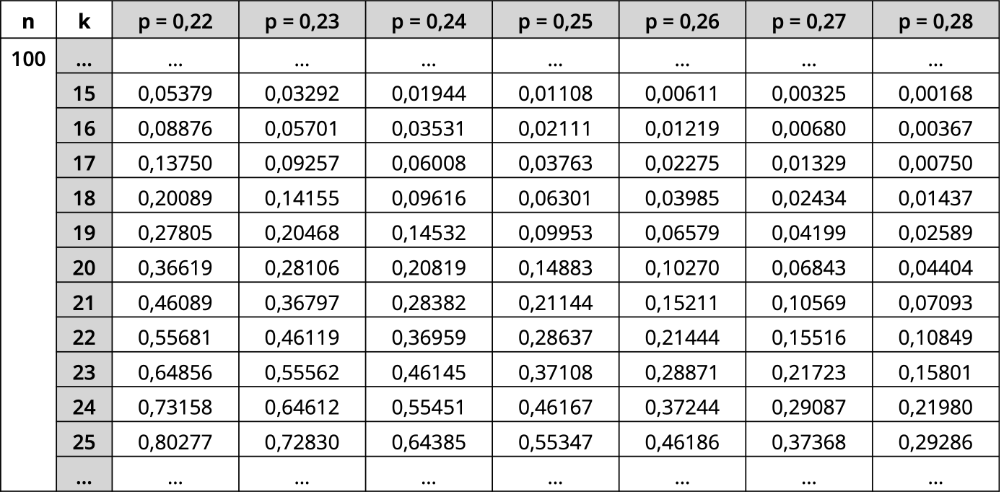
Hinweis: Die unten abgebildete Tabelle ergänzt das zugelassene Tafelwerk.
Binomialverteilung kumulativ; \(k \mapsto \sum \limits_{i\,=\,0}^k B(n;p;i)\)
(5 BE)
Lösung zu Teilaufgabe 2d
Anteil der Radausflügler
\(Y\): Anzahl der Radausflügler unter einer Stichprobe von 100 Touristen.
„In diesem Fall wird die Nullhypothese abgelehnt, wenn sich unter diesen mehr als 20 Radausflügler befinden."
Annahmebereich \(A = \{0;1;2; \dots;20\}\)
Ablehnungsbereich \(\textcolor{#cc071e}{\overline{A} = \{21;22; \dots;100\}}\)
„Damit die Wahrscheinlichkeit für den Fehler zweiter Art höchstens 30 % beträgt, ..."
„... muss der tatsächliche Anteil der Radausflügler unter allen Touristen mindestens einen bestimmten Wert haben.
Die Wahrscheinlichkeit für den Fehler 2. Art kann nur berechnet werden, wenn für eine Gegenhypothese \(H_1\) eine Wahrscheinlichkeit \(p_1\) angenommen wird.
In diesem Fall ist derjenige Wert von \(\textcolor{#e9b509}{p_1}\) gesucht, der für die Gegenhypothese \(H_1\colon p \textcolor{#e9b509}{> 0{,}15}\) mindestens zu wählen ist, damit die Wahrscheinlichkeit für den Fehler 2. Art höchstens 30 % beträgt.
Da die Entscheidung über die Annahme oder Ablehnung einer Nullhypothese aufgrund eines zufälligen Ergebnisses einer Stichprobe erfolgt, kann es zu Fehlentscheidungen kommen.
Fehler 1. Art und Fehler 2. Art
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Fehler 2. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich nicht abgelehnt.
| \(H_{0}\) ist wahr | \(H_{0}\) ist falsch | |
| \(H_{0}\) wird abgelehnt | Fehler 1. Art | richtige Entscheidung |
| \(H_{0}\) wird nicht abgelehnt | richtige Entscheidung | Fehler 2. Art |
Wahrscheinlichkeit \(\boldsymbol{\alpha'}\) für den Fehler 1. Art
\[\alpha' = P(\text{Fehler 1. Art}) = P^{n}_{p_0} (X \in K)\]
Wahrscheinlichkeit \(\boldsymbol{\beta'}\) für den Fehler 2. Art
\[\beta' = P(\text{Fehler 2. Art}) = P^n_{p_{1}} (X \in \overline{K})\]
Um die Wahrscheinlichkeit für den Fehler 2. Art berechnen zu können, muss eine Annahme für die Wahrscheinlichkeit \(p_1\) der Gegenhypothese \(H_1\) getroffen werden.
Die Wahrscheinlichkeit für den Fehler 2. Art kann weit über 50 % betragen. Deshalb lässt sich nicht folgern, dass die Nullhypothese tatsächlich gilt, nur weil sie nicht abgelehnt wird.
\(K\): kritischer Bereich (Ablehnungsbereich) der Nullhypothese
\(\overline{K}\): nichtkritischer Bereich der Nullhypothese
\[\begin{align*}P(\text{Fehler 2. Art}) &\textcolor{#0087c1}{\leq} \textcolor{#0087c1}{0{,}3} &&| \; H_0 \; \text{wird nicht abgelehnt,}\;\textcolor{#e9b509}{\text{obwohl sie falsch ist}} \\[0.8em] P_{\textcolor{#e9b509}{p_1}}^{100}(Y \in A) &\textcolor{#0087c1}{\leq} \textcolor{#0087c1}{0{,}3} &&| \; A= \{0;1;2; \dots;20\} \\[0.8em] P_{\textcolor{#e9b509}{p_1}}^{100}(Y \leq 20) &\textcolor{#0087c1}{\leq} \textcolor{#0087c1}{0{,}3}\end{align*}\]
Mithilfe der beigefügten Tabelle, wählt man nun für \(k = 20\) den kleinstmöglichen Wert \(p\), sodass die Bedingung \(P_{\textcolor{#e9b509}{p_1}}^{100}(Y \leq 20) \textcolor{#0087c1}{\leq} \textcolor{#0087c1}{0{,}3}\) erfüllt ist.
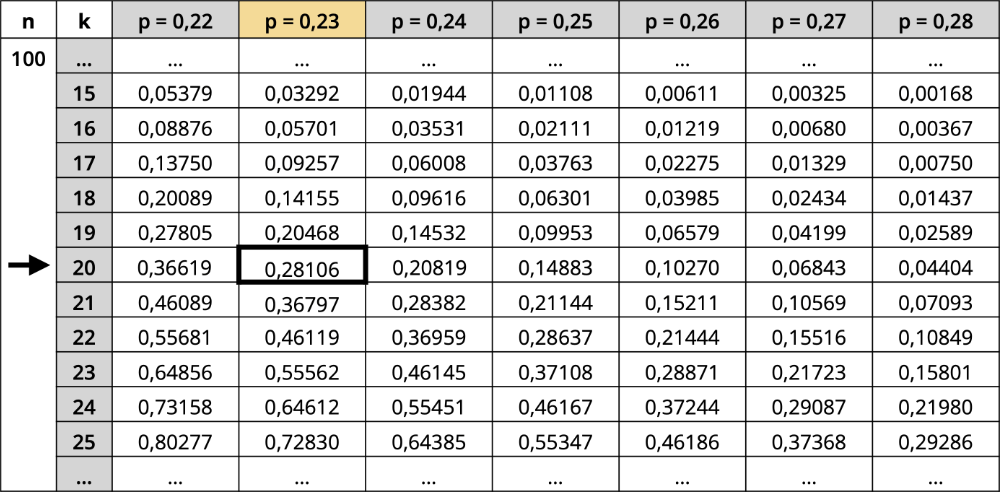
\[P_{\textcolor{#e9b509}{p_1}}^{100}(Y \leq 20) \textcolor{#0087c1}{\leq} \textcolor{#0087c1}{0{,}3} \overset{\text{Tabelle}}{\Rightarrow} \textcolor{#e9b509}{p_1 = 0{,}23 = 23\,\%}\]
mit \(P_{\textcolor{#e9b509}{0{,}23}}^{100}(Y \leq 20) = 0{,}28106 \textcolor{#0087c1}{\leq} \textcolor{#0087c1}{0{,}3}\) (vgl. Tabelle)
Damit die Wahrscheinlichkeit für den Fehler zweiter Art höchstens 30 % beträgt, muss der tatsächliche Anteil der Radausflügler unter allen Touristen mindestens 23 % sein.
Fehler 2. Art im Sachzusammenhang
Obwohl der Anteil der Radausflügler mehr als 15 % beträgt (Nullhypothese ist falsch), werden die Shuttlebusses nicht weiter betrieben (Nullhypothese wird nicht abgelehnt).


