Mithilfe der Graphologie werden aus der Handschrift einer Person Rückschlüsse auf deren Persönlichkeit gezogen.
An einer Fachschule für Graphologie ist eine Dozentenstelle neu zu besetzen. Den Bewerbern sollen im Rahmen eines Vortests Schriftproben vorgelegt werden. Jede Schriftprobe stammt entweder von einer entscheidungsfreudigen oder von einer zögerlichen Person; dies soll dem jeweiligen Bewerber mitgeteilt werden, der sich anschließend bei jeder Schriftprobe entscheiden muss, ob er sie einer entscheidungsfreudigen oder einer zögerlichen Person zuordnet. Ein Bewerber soll den Vortest bestehen, wenn er sich bei mehr als zwei Dritteln der vorgelegten Schriftproben richtig entscheidet.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass ein Bewerber, der nur rät, den Vortest besteht, wenn man ihm zwölf Schriftproben vorlegen würde.
(5 BE)
Lösung zu Teilaufgabe 1a
Zufallsgröße \(X \colon \enspace\)„Anzahl der richtig beurteilten Schriftproben"
Analyse der Angabe:
"... von zwölf vorgelegten Schriftproben ..."
\[\Longrightarrow \quad n = 12\]
"... wenn er nur rät."
\[\Longrightarrow \quad p = 0{,}5\]
"... mehr als zwei Drittel von zwölf vorgelegten Stichproben ..."
\[\frac{2}{3} \cdot 12 = 8 \quad \Longrightarrow \quad X \geq 9\]
Binomialverteilung
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
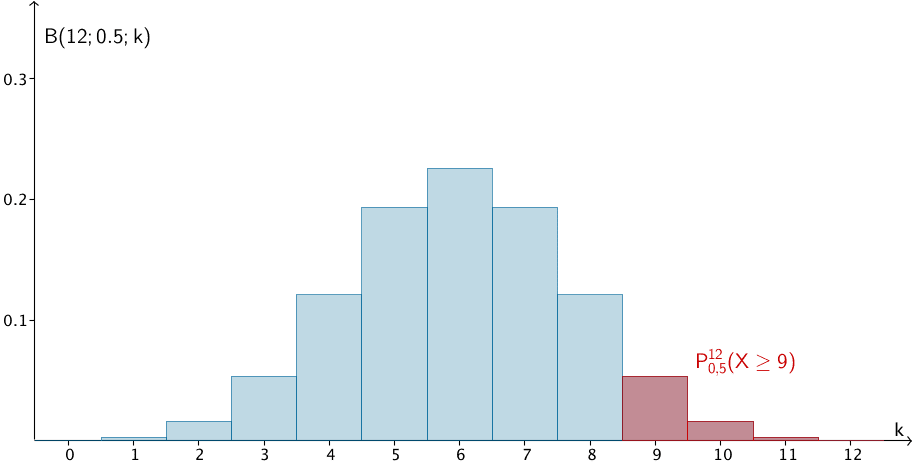
Die Zufallsgröße \(X\) ist nach \(B(12;0{,}5)\) binomialverteilt.
Da das Stochastische Tafelwerk mit Abiturzulassung keine Binomialverteilung für \(n = 12\) tabellarisert, kann das Prinzip "Betrachten des Gegenereignisses" \(\left(P^{12}_{0{,}5} (X \geq 9) = 1 - P^{12}_{0{,}5} (X \leq 8)\right)\) nicht angewendet werden.
Stattdessen muss die Summe \(P^{12}_{0{,}5} (X \geq 9) = \sum \limits_{i \, = \, 9}^{12} B(12; {0{,}5}; i)\) errechnet werden.
Anwenden der Formel von Bernoulli:
Formel von Bernoulli
Wahrscheinlichkeit für genau \(k\) Treffer bei einer Bernoullikette der Länge \(n\) und der Trefferwahrscheinlichkeit \(p\) für das Eintreten eines betrachteten Ereignisses:
\[P(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^k \cdot (1 - p)^{n - k}\]
\[k \in \{0,1,\dots,n\}\]
\[\begin {align*} P^{12}_{0{,}5} (X \geq 9) \quad &= & &\sum \limits_{i \, = \, 9}^{12} B(12; {0{,}5}; i) \\[0.8em] &= & &B(12; {0{,}5}; 9) + B(12; {0{,}5}; 10) + B(12; {0{,}5}; 11) + B(12; {0{,}5}; 12) \\[0.8em] &= & &\binom{12}{9} \cdot 0{,}5^9 \cdot (1 - 0{,}5)^{12 - 9} \\[0.8em] & &+ \quad &\binom{12}{10} \cdot 0{,}5^{10} \cdot (1 - 0{,}5)^{12 - 10} \\[0.8em] & &+ \quad &\binom{12}{11} \cdot 0{,}5^{11} \cdot (1 - 0{,}5)^{12 - 11} \\[0.8em] & &+ \quad &\binom{12}{12} \cdot 0{,}5^{12} \cdot (1 - 0{,}5)^{12 - 12} \\[0.8em] &= & &\binom{12}{9} \cdot \underbrace{0{,}5^9 \cdot 0{,}5^3}_{0{,}5^{12}} \\[0.8em] & &+ \quad &\binom{12}{10} \cdot \underbrace{0{,}5^{10} \cdot 0{,}5^2}_{0{,}5^{12}} \\[0.8em] & &+ \quad &\binom{12}{11} \cdot \underbrace{0{,}5^{11} \cdot 0{,}5^1}_{0{,}5^{12}} \\[0.8em] & &+ \quad &\binom{12}{12} \cdot \underbrace{0{,}5^{12} \cdot 0{,}5^0}_{0{,}5^{12}} \\[0.8em] &= & &\left [ \binom{12}{9} + \binom{12}{10} + \binom{12}{11} + \binom{12}{12} \right ] \cdot 0{,}5^{12} \\[0.8em] &\approx & &0{,}073 = 7{,}3 \; \% \end{align*}\]
Der Bewerber würde den Vortest mit einer Wahrscheinlichkeit von ca. 7,3 % bestehen, wenn er bei der Beurteilung der Schriftproben nur rät.