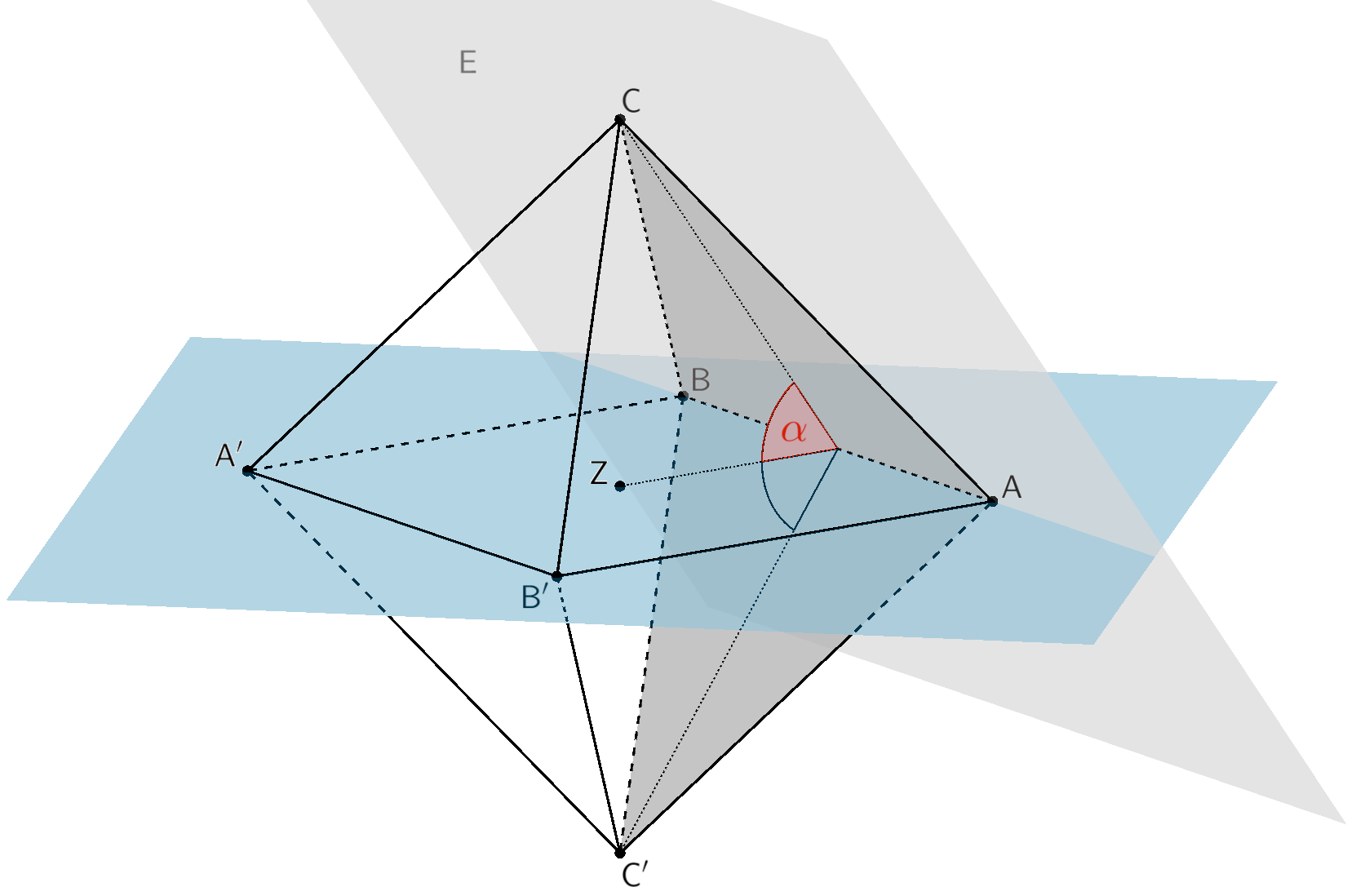
Bestimmen Sie die Größe des Winkels zwischen den Seitenflächen \(ABC\) und \(AC'B\).
(4 BE)
Lösung zu Teilaufgabe e
Schnittwinkel zweier Ebenen, Trigonometrie - rechtwinkliges Dreieck
1. Lösungsansatz: Schnittwinkel zweier Ebenen
Der Punkt \(C'\) geht durch Spiegelung des Punktes \(C\) am Punkt \(Z\) hervor. Folglich geht die Seitenfläche \(AC'B\) durch Spiegelung der Seitenfläche \(ABC\) an der Ebene hervor, in der die Punkte \(A\), \(B\) und \(Z\) liegen. Der Winkel zwischen den Seitenflächen \(ABC\) und \(AC'B\) entspricht somit dem Doppelten des Schnittwinkels \(\alpha\) der Ebene \(E\), in der die Punkte \(A\), \(B\) und \(C\) liegen, und der Ebene, in der die Punkte \(A\), \(B\) und \(Z\) liegen (vgl. Teilaufgaben a,b).
Der Schnittwinkel \(\alpha\) lässt sich mithilfe der Normalenvektoren der beiden Ebenen berechnen.
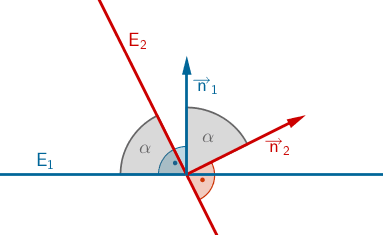
Schnittwinkel \(\boldsymbol{\alpha}\) zweier Ebenen
\[E_1\colon \enspace \overrightarrow{n}_1 \circ \left( \overrightarrow{X} - \overrightarrow{A} \right) = 0\]
\[E_2\colon \enspace \overrightarrow{n}_2 \circ \left( \overrightarrow{X} - \overrightarrow{B} \right) = 0\]
\[\cos \alpha = \frac{\vert \overrightarrow{n}_1 \circ \overrightarrow{n}_2 \vert}{\vert \overrightarrow{n}_1 \vert \cdot \vert \overrightarrow{n}_2 \vert} \enspace \Rightarrow \enspace \alpha = \cos^{-1}(\dots)\]
\[(0^{\circ} \leq \alpha \leq 90^{\circ})\]
Aus den Teilaufgabe a,b sind die Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}\) der Ebene \(E\) bzw. der Ebene, in der die Punkte \(A\), \(B\) und \(Z\) liegen, bereits bekannt.
\(\overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}\), \(\overrightarrow{n} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\)
Schnittwinkel \(\alpha\) der Ebene \(E\) und der Ebene, in der die Punkte \(A\), \(B\) und \(Z\) liegen, berechnen:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \cos \alpha &= \frac{\left| \overrightarrow{n}_{E} \circ \overrightarrow{n} \right|}{\left| \overrightarrow{n}_{E} \right| \cdot \left| \overrightarrow{n} \right|} \\[0.8em] &= \frac{\left| \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|}{\left| \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert 1 \cdot 0 + 1 \cdot 0 + 1 \cdot 1 \vert}{\sqrt{1^{2} + 1^{2} + 1^{2}} \cdot \sqrt{0^{2} + 0^{2} + 1^{2}}} \\[0.8em] &= \frac{1}{\sqrt{3}} \\[0.8em] &= \frac{\sqrt{3}}{3} & &| \; \text{TR:} \; \cos^{-1}(\dots) \\[3.2em] \alpha &\approx 54{,}74^{\circ}\end{align*}\]
Größe des Winkels berechnen, den Die Seitenflächen \(ABC\) und \(AC'B\) einschließen:
\[2 \cdot \alpha = 2 \cdot 54{,}74^{\circ} = 109{,}48^{\circ}\]
Die Seitenflächen \(ABC\) und \(AC'B\) schließen einen Winkel von ca. 109,48° ein.
2. Lösungsansatz: Trigonometrie - rechtwinkliges Dreieck
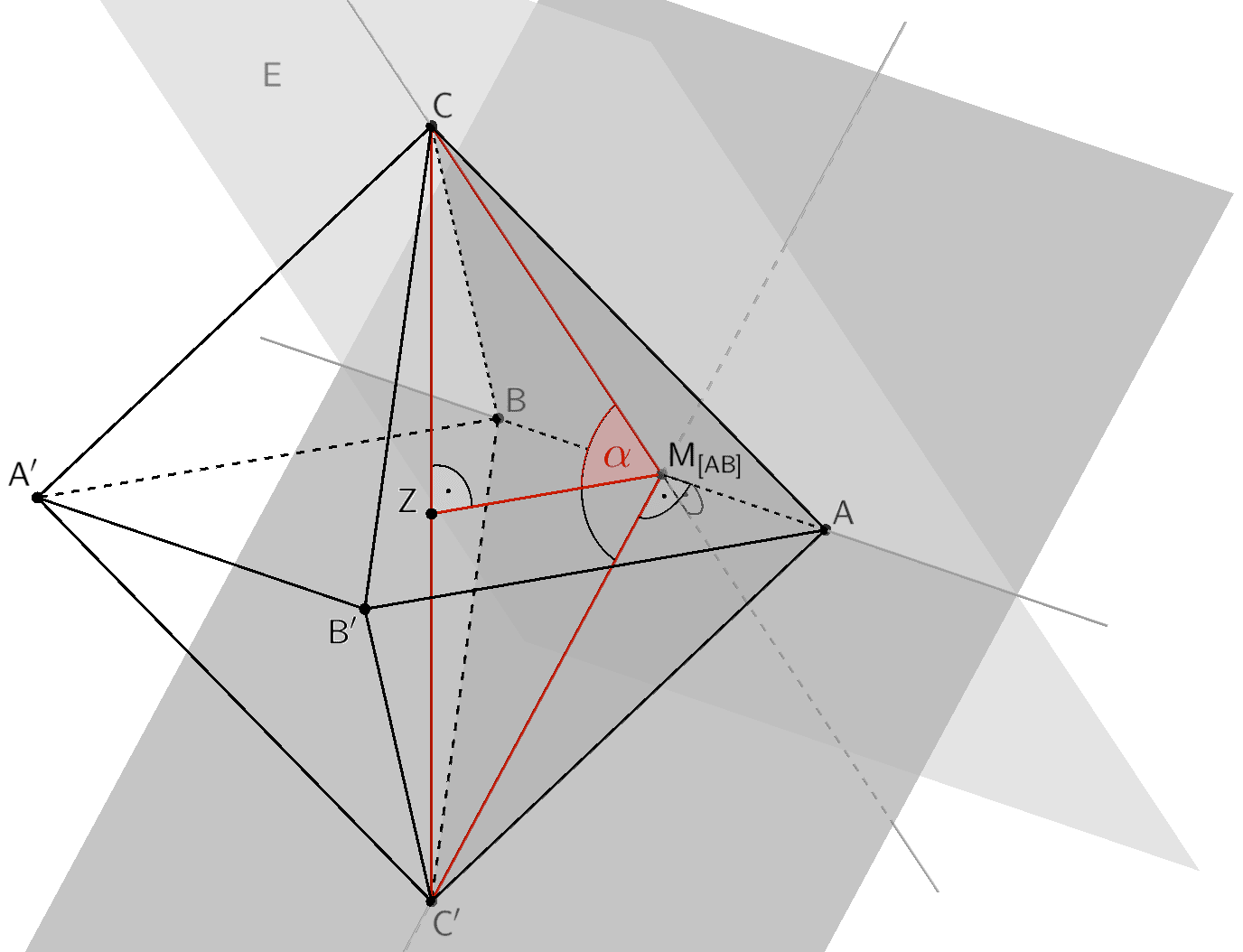
Unter dem Schnittwinkel zweier Ebenen versteht man den spitzen Winkel zwischen zwei Geraden, welche in demselben Punkt auf der Schnittgeraden der Ebenen senkrecht stehen und jeweils in einer der beiden Ebenen liegen.
Im vorliegenden Fall ist dieser Punkt beispielsweise der Mittelpunkt \(M_{[AB]}\) der Strecke \([AB]\), wobei die Gerade \(AB\) die Schnittgerade der Ebenen ist, in denen die Seitenflächen \(ABC\) und \(AC'B\) liegen. Der Mittelpunkt \(M_{[AB]}\) ist jeweils der Lotfußpunkt (Höhenfußpunkt) des Punktes \(C\) bzw. \(C'\) auf die Seite \([AB]\) des gleichschenkligen Dreiecks \(ABC\) bzw. \(AC'B\) mit der Basis \([AB]\). Damit lässt sich das gleichschenklige Dreieck \(CC'M_{[AB]}\) mit der Basis \([CC']\) konstruieren, welches in zwei kongruente rechtwinklige Dreiecke \(CZM_{[AB]}\) und \(ZC'M_{[AB]}\) zerlegt werden kann.
Die Größe des Winkels zwischen den Seitenflächen \(ABC\) und \(AC'B\) ergibt sich als das Doppelte des Winkels \(\measuredangle CM_{[AB]}Z = \alpha\) im rechtwinkligen Dreieck \(CZM_{[AB]}\).
Trigonometrische Beziehungen im rechtwinkligen Dreieck
\[\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}\]
\[\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}\]
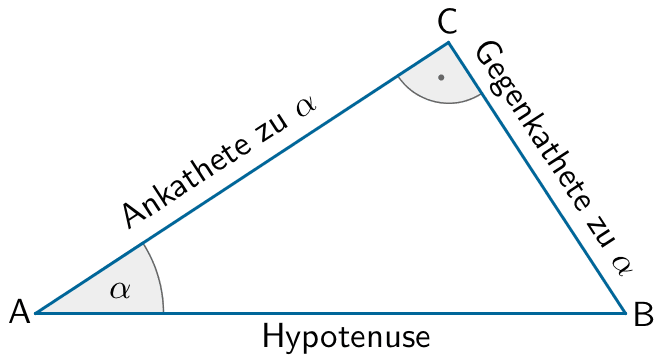
\[\tan \alpha = \frac{\overline{CZ}}{\overline{ZM_{[AB]}}}\]
Mittelpunkt \(M_{[AB]}\) der Strecke \([AB]\) berechnen:
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\(A(6|3|3)\), \(B(3|6|3)\)
\[\begin{align*}\overrightarrow{M_{[AB]}} &= \frac{1}{2} \cdot \left( \overrightarrow{A} + \overrightarrow{B} \right) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 6 \\ 3 \\ 3 \end{pmatrix} + \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} \right] \\[0.8em] &= \frac{1}{2} \cdot \begin{pmatrix} 9 \\ 9 \\ 6 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 4{,}5 \\ 4{,}5 \\ 3 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad M_{[AB]}(4{,}5|4{,}5|3)\]
Längen der Strecken \([CZ]\) und \([ZM_{[AB]}]\) berechnen:
Ggf. ist die Länge der Strecke \([CZ]\) aus Teilaufgabe 1d bereits bekannt (Höhe der Pyramide ABA'B'C).
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\(C(3|3|6)\), \(Z(3|3|3)\), \(M_{[AB]}(4{,}5|4{,}5|3)\)
\[\begin{align*}\overline{CZ} &= \left| \overrightarrow{CZ} \right| \\[0.8em] &= \left| \overrightarrow{Z} - \overrightarrow{C} \right| \\[0.8em] &= \left| \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} - \begin{pmatrix} 3 \\ 3 \\ 6 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 0 \\ -3 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^{2} + 0^{2} + (-3)^{2}} \\[0.8em] &= \sqrt{9} \\[0.8em] &= 3 \end{align*}\]
\[\begin{align*}\overline{ZM_{[AB]}} &= \left| \overrightarrow{ZM_{[AB]}} \right| \\[0.8em] &= \left| \overrightarrow{M_{[AB]}} - \overrightarrow{Z} \right| \\[0.8em] &= \left| \begin{pmatrix} 4{,}5 \\ 4{,}5 \\ 3 \end{pmatrix} - \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \sqrt{{1{,}5}^{2} + {1{,}5}^{2} + 0^{2}} \\[0.8em] &= \sqrt{4{,}5} \\[0.8em] &= \frac{3\sqrt{2}}{2} \end{align*}\]
Maß \(\alpha\) des Winkels \(\measuredangle CM_{[AB]}Z\) berechnen:
\[\tan \alpha = \frac{\overline{CZ}}{\overline{ZM_{[AB]}}} = \frac{\cancel{3}}{\frac{\cancel{3}\sqrt{2}}{2}} = \frac{2}{\sqrt{2}} = \sqrt{2} \qquad |\; \text{TR:} \; \tan^{-1}(\dots)\]
\[\alpha \approx 54{,}74^{\circ}\]
Größe des Winkels berechnen, den Die Seitenflächen \(ABC\) und \(AC'B\) einschließen:
\[2 \cdot \alpha = 2 \cdot 54{,}74^{\circ} = 109{,}48^{\circ}\]
Die Seitenflächen \(ABC\) und \(AC'B\) schließen einen Winkel von ca. 109,48° ein.