Dem Flächenstück, das \(G_h\) mit der \(x\)-Achse vollständig einschließt, werden Rechtecke so einbeschrieben, dass jeweils eine Seite des Rechtecks auf der \(x\)-Achse liegt. Berechnen Sie den größtmöglichen Flächeninhalt \(A\) eines solchen Rechtecks.
(Ergebnis: \(A = \frac{16}{9}\sqrt{3}\))
(6 BE)
Lösung zu Teilaufgabe 1b
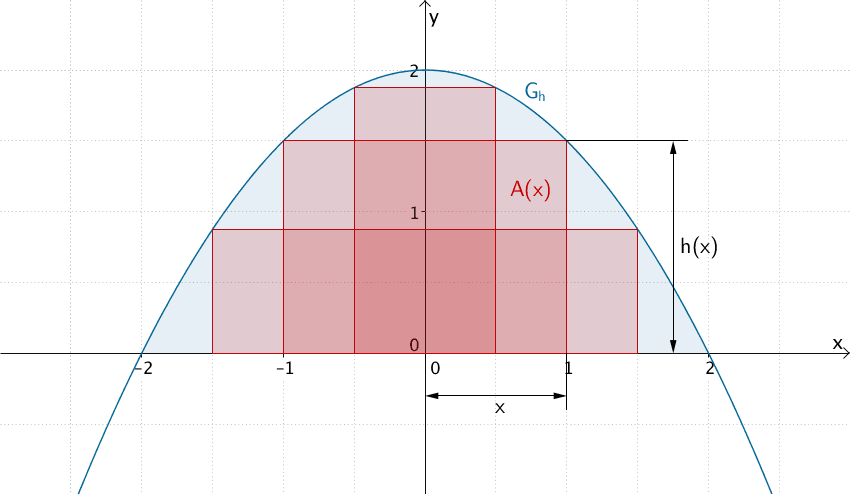
Flächenstück, das \(G_{h}\) mit der \(x\)-Achse einschließt und Beispiele einbeschriebener Rechtecke
Flächeninhalt \(A\) der einbeschriebenen Rechtecke in Abhängigkeit von \(x\) bestimmen:
\[h(x) = -\frac{1}{2}x^2 + 2\,; \quad D = \mathbb R\]
\[\begin{align*} A(x) &= 2 \cdot x \cdot h(x) & & x \in [0; 2] \\[0.8em] &= 2x \cdot \left ( -\frac{1}{2}x^2 + 2 \right ) \\[0.8em] &= -x^3 + 4x \end{align*}\]
Notwendige Bedingung für maximalen Flächeninhalt:
\[A'(x) \overset{!}{=} 0\]
Erste Ableitung \(A'\) bilden:
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[A'(x) = -3x^2 +4\]
\[\begin{align*}A'(x) \overset{!}{=} 0 \quad \Longrightarrow \quad -3x^2 + 4 &= 0 & &| -4 \\[0.8em] -3x^2 &= -4 & &| :(-3) \\[0.8em] x^2 &= \frac{4}{3} & &| \; \sqrt{\quad} \quad x \in [0;2] \\[0.8em] x &= \frac{2}{\sqrt{3}} & &| \cdot \frac{\sqrt{3}}{\sqrt{3}} \\[0.8em] x &= \frac{2}{3}\sqrt{3} \end{align*}\]
Für \(x = \frac{2}{3}\sqrt{3}\) ist der Flächeninhalt \(A\) des einbeschriebenen Rechtecks extremal.
Art des Extremums nachweisen:
Der Nachweis der Art des Extremums kann mithilfe des Monotoniekriterium oder mithilfe der zweiten Ableitung \(A''\) erfolgen.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[\left. \begin{align*} &A'(x) > 0 \enspace \text{für} \enspace x < \frac{2}{3}\sqrt{3} \\[0.8em] &A'({\textstyle \frac{2}{3}\sqrt{3}}) = 0 \\[0.8em] &A'(x) < 0 \enspace \text{für} \enspace x > \frac{2}{3}\sqrt{3} \end{align*} \right\} \enspace \Rightarrow \enspace \text{lokales Maximum}\]
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
Zweite Ableitung \(A''\) bilden:
\[A'(x) = -3x^2 +4\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[A''(x) = -6x\]
\[A''({\textstyle \frac{2}{3}\sqrt{3}}) = -6 \cdot \frac{2}{3}\sqrt{3} = -4 \sqrt{3}\]
\[\left. \begin{align*} &A'({\textstyle \frac{2}{3}\sqrt{3}}) = 0 \\[0.8em] &A''({\textstyle \frac{2}{3}\sqrt{3}}) < 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{lokales Maximum}\]
Größtmöglichen Flächeninhalt \(A\) berechnen:
\[A(x) = -x^3 + 4x\]
\[\begin{align*} A({\textstyle \frac{2}{3}\sqrt{3}}) &= - \left (\frac{2}{3}\sqrt{3} \right)^3 + 4 \cdot \frac{2}{3}\sqrt{3} \\[0.8em] &= -\frac{8}{9}\sqrt{3} + \frac{8}{3}\sqrt{3} \\[0.8em] &= -\frac{8}{9}\sqrt{3} + \frac{24}{9}\sqrt{3} \\[0.8em] &= \frac{16}{9}\sqrt{3} \end{align*}\]
De Flächeninhalt \(A\) des größtmöglichen einbeschriebenen Rechtecks beträgt \(\frac{16}{9}\sqrt{3}\) FE (Flächeneinheiten).
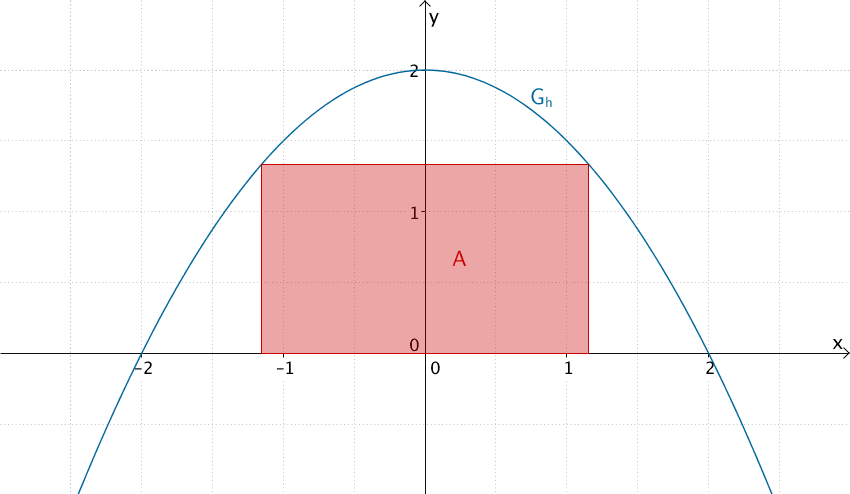
Größtmögliches einbeschriebenes Rechteck mit Flächeninhalt \(A\)


