Rechenregeln für Grenzwerte von Funktionen
- \(\displaystyle \lim \limits_{x \, \to \, x_{0}} \left[C \cdot f(x)\right] = C \cdot \left( \lim_{x \, \to \, x_{0}} f(x) \right) \qquad\) (\(C\): Konstante)
- \[\lim \limits_{x \, \to \, x_{0}} \left[f(x) \pm g(x)\right] = \lim \limits_{x \, \to \, x_{0}} f(x) \pm \lim \limits_{x \, \to \, x_{0}} g(x)\]
- \[\lim \limits_{x \, \to \, x_{0}} \left[f(x) \cdot g(x)\right] = \left( \lim \limits_{x \, \to \, x_{0}} f(x) \right) \cdot \left( \lim \limits_{x \, \to \, x_{0}} g(x) \right)\]
- \[\lim \limits_{x \, \to \, x_{0}} \left[ \frac{f(x)}{g(x)} \right] = \frac{\lim \limits_{x \, \to \, x_{0}} f(x)}{\lim \limits_{x \, \to \, x_{0}} g(x)} \qquad \left( \lim \limits_{x \, \to \, x_{0}} g(x) \neq 0 \right)\]
- \[\lim \limits_{x \, \to \, x_{0}} \sqrt[n]{f(x)} = \sqrt[n]{\lim \limits_{x \, \to \, x_{0}} f(x)}\]
- \[\lim \limits_{x \, \to \, x_{0}} \left[f(x)\right]^{n} = \left( \lim \limits_{x \, \to \, x_{0}} f(x) \right)^{n}\]
- \[\lim \limits_{x \, \to \, x_{0}} \big[a^{f(x)}\big] = a^{\left( \lim \limits_{x \, \to \, x_{0}} f(x) \right)}\]
- \[\lim \limits_{x \, \to \, x_{0}} \left[ \log_{a}{f(x)} \right] = \log_{a}{\left( \lim \limits_{x \, \to \, x_{0}} f(x) \right)}\]
Die Regeln gelten auch für die Grenzwertbetrachtungen \(x \to -\infty\) und \(x \to \infty\).
Wichtige Grenzwerte (vgl. Merkhilfe)
\[\lim \limits_{x \, \to \, +\infty} \frac{x^{r}}{e^{x}} = 0\]
Für \(x \to +\infty\) wächst \(e^{x}\) schneller als \(x^{r}\).
\[\lim \limits_{x \, \to \, +\infty} \frac{\ln{x}}{x^{r}} = 0\]
Für \(x \to +\infty\) wächst \(x^{r}\) schneller als \(\ln{x}\).
\[\lim \limits_{x \, \to \, 0} \left(x^{r} \cdot \ln{x}\right) = 0\]
vgl. Rechenregeln für Grenzwerte von Funktionen
(jeweils \(r > 0\))
Regel von L'Hospital
Führt der Grenzwert \(\,\displaystyle \lim \limits_{x\,\to\,x_0} \frac{f(x)}{g(x)}\,\) auf den unbestimmten Ausdruck \(\displaystyle \,\frac{0}{0}\,\) oder \(\displaystyle \,\frac{\infty}{\infty}\,\),
und existiert der Grenzwert \(\displaystyle \,\lim \limits_{x\,\to\,x_0} \frac{f'(x)}{g'(x)}\,\), so gilt:
\[\lim \limits_{x\,\to\,x_0} \frac{f(x)}{g(x)} = \lim \limits_{x\,\to\,x_0} \frac{f'(x)}{g'(x)}\]
Falls erforderlich. kann die Regel mehrmals (hintereinander) angewendet werden.
Die Regel gilt auch für die Grenzwertbetrachtungen \(\,x \to -\infty\,\) oder \(\,x \to \infty\,\).
Anmerkung:
Die Regel von L'Hospital ist nicht im G8 Mathematik Lehrplan enthalten. Erfahrungsgemäß wird diese aber des Öfteren optional unterrichtet, um Grenzwertbetrachtungen von unbestimmten Ausdrücken der Form \(\dfrac{0}{0}\) oder \(\dfrac{\infty}{\infty}\) zu vertiefen.
Beispiel:
Mit der in \(\mathbb R\) definierten Funktion \(\displaystyle f \colon x \mapsto \dfrac{2x^{3}}{e^{0{,}5x}}\) sei die Grenzwertbetrachtung \(x \to +\infty\) durchzuführen.
Unter Berücksichtigung des wichtigen Grenzwerts \(\displaystyle \lim \limits_{x \, \to \, +\infty} \frac{x^{r}}{e^{x}} = 0\) gilt:
\[\lim \limits_{x \, \to \, +\infty} f(x) = \lim \limits_{x \, \to \, +\infty} \frac{2x^{3}}{e^{0{,}5x}} = 2 \cdot \lim \limits_{x \, \to \, +\infty} \dfrac{x^{3}}{e^{0{,}5x}} = 0 \]
Der Grenzwert kann durch mehrmaliges Anwenden der Regel von L'Hospital bestätigt werden.
\[f(x) \frac{2x^{3}}{e^{0{,}5x}}; \; D_{f} = \mathbb R\]
Die Grenzweltbetrachtung \(\displaystyle \lim \limits_{x \, \to \, +\infty} \frac{2x^{3}}{e^{0{,}5x}}\) führt auf den unbestimmten Ausdruck \(\frac{\infty}{\infty}\). In diesem Fall muss die Regel von L'Hospital dreimal hintereinander angewendet werden, um einen Ausdruck der Form \(\frac{C}{\infty}\) zu erhalten, wobei \(C\) eine Konstante ist. Hierfür wird der Zählerterm und der Nennerterm jeweils dreimal abgeleitet (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
Ableitungen des Zählerterms \(2x^{3}\):
\[\left( 2x^{3} \right)' = 6x^{2}\]
\[\left( 2x^{3} \right)'' = 12x\]
\[\left( 2x^{3} \right)''' = 12\]
Ableitungen des Nennerterms \(e^{0{,}5x}\):
\[\left(e^{0{,}5x}\right)' = 0{,}5e^{0{,}5}\]
\[\left(e^{0{,}5x}\right)'' = 0{,}25e^{0{,}5}\]
\[\left(e^{0{,}5x}\right)''' = 0{,}125e^{0{,}5}\]
Damit ergibt sich:
\[\begin{align*} \lim \limits_{x \, \to \, +\infty} f(x) &= \lim \limits_{x \, \to \, +\infty} \underbrace{\frac{2x^{3}}{e^{0{,}5x}}}_{\Large \frac{\infty}{\infty}} & &|\;\text{Regel v. L'Hospital anwenden} \\[0.8em] &= \lim \limits_{x \, \to \, +\infty} \underbrace{\frac{6x^{2}}{0{,}5e^{0{,}5x}}}_{\Large \frac{\infty}{\infty}} & &|\;\text{Regel v. L'Hospital anwenden} \\[0.8em] &= \lim \limits_{x \, \to \, +\infty} \underbrace{\frac{12x}{0{,}25e^{0{,}5x}}}_{\Large \frac{\infty}{\infty}} & &|\;\text{Regel v. L'Hospital anwenden} \\[0.8em] &= \lim \limits_{x \, \to \, +\infty} \frac{12}{0{,}125e^{0{,}5x}} \\[0.8em] &= \lim \limits_{x \, \to \, +\infty} \underbrace{\frac{96}{e^{0{,}5x}}}_{\Large \frac{C}{\infty}} \\[0.8em] &= 0 \end{align*}\]
Beispielaufgabe
Gegeben seien die Funktionen \(f \colon x \mapsto \dfrac{1}{x^{2} - 4}\) und \(g \colon x \mapsto \ln{[f(x)]}\). Bestimmen Sie die maximale Definitionsmenge \(D_{g}\) der Funktion \(g\) und untersuchen Sie das Verhalten von \(g\) an den Grenzen von \(D_{g}\).
Maximale Definitionsmenge \(D_{g}\) der Funktion \(g\)
\[f(x) = \frac{1}{x^{2} - 4}\]
\[g(x) = \ln{[f(x)]}\]
Die (Natürliche) Logarithmusfunktion ist in \(\mathbb R^{+}\) definiert.
\[\begin{align*}\Longrightarrow \quad f(x) > 0 \quad \Longrightarrow \quad x^{2} - 4 &> 0 & &| + 4 \\[0.8em] x^{2} &> 4 & &| \; \sqrt{\enspace} \\[0.8em] \vert x \vert &> 2 \end{align*}\]
\[\begin{align*}\Longrightarrow \quad x > 2 \enspace \vee \enspace -x &> 2 & & | \cdot (-1) \\[0.8em] x &< -2 \end{align*}\]
\[\Longrightarrow \quad D_{g} = ]-\infty;-2[\; \cup \; ]2;+\infty[ \; = \mathbb R \,\backslash\, [-2;2]\]
Verhalten der Funktion \(g\) an den Grenzen von \(D_{g}\)
\[f(x) = \frac{1}{x^{2} - 4}\]
\[g(x) = \ln{[f(x)]}\]
Das Verhalten der Funktion \(g\) an den Grenzen von \(D_{g}\) hängt vom Verhalten der Funktion \(f\) ab. Es wird zuerst das Verhalten der Funktion \(f\) an den Grenzen von \(D_{g}\) untersucht und daraus das Verhalten der Funktion \(g\) gefolgert.
Verhalten der Funktion \(g\) für \(x \to -2^{-}\) und \(x \to 2^{+}\)
\[\lim \limits_{x \, \to \, -2^{-}} f(x) = \lim \limits_{x \, \to \, -2^{-}} \frac{1}{x^{2} - 4} = \lim \limits_{x \, \to \, -2^{-}} \frac{1}{\underbrace{(x - 2)(x + 2)}_{\to \, 0^{+}}} = +\infty\]
\[\lim \limits_{x \, \to \, -2^{-}} g(x) = \lim \limits_{x \, \to \, -2^{-}} \ln{[\underset{\to \, + \infty}{f(x)}]} = +\infty\]
\[\lim \limits_{x \, \to \, 2^{+}} f(x) = \lim \limits_{x \, \to \, 2^{+}} \frac{1}{x^{2} - 4} = \lim \limits_{x \, \to \, 2^{+}} \frac{1}{\underbrace{(x - 2)(x + 2)}_{\to \, 0^{+}}} = +\infty\]
\[\lim \limits_{x \, \to \, 2^{+}} g(x) = \lim \limits_{x \, \to \, 2^{+}} \ln{[\underset{\to \, + \infty}{f(x)}]} = +\infty\]
Verhalten der Funktion \(g\) für \(x \to -\infty\) und \(x \to +\infty\)
\[\lim \limits_{x \, \to \, -\infty} f(x) = \lim \limits_{x \, \to \, -\infty} \frac{1}{\underbrace{x^{2} - 4}_{\to \, +\infty}} = 0^{+}\]
\[\lim \limits_{x \, \to \, -\infty} g(x) = \lim \limits_{x \, \to \, -\infty} \ln{[\underset{\to \, 0^{+}}{f(x)}]} = -\infty\]
\[\lim \limits_{x \, \to \, +\infty} f(x) = \lim \limits_{x \, \to \, +\infty} \frac{1}{\underbrace{x^{2} - 4}_{\to \, +\infty}} = 0^{+}\]
\[\lim \limits_{x \, \to \, +\infty} g(x) = \lim \limits_{x \, \to \, +\infty} \ln{[\underset{\to \, 0^{+}}{f(x)}]} = -\infty\]
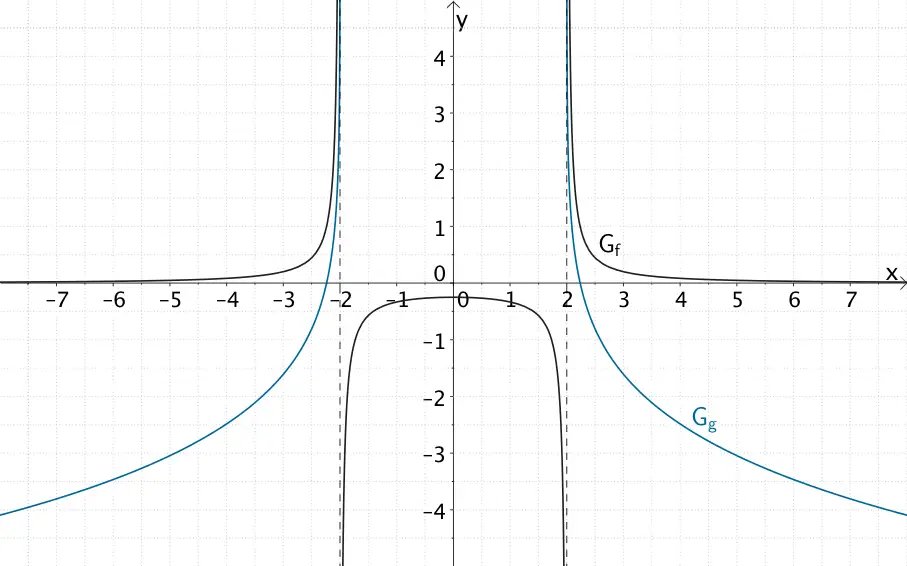
Verlauf des Graphen \(G_{f}\) der Funktion \(f \colon x \mapsto \dfrac{1}{x^{2} - 4}\) und Verlauf des Graphen \(G_{g}\) der Funktion \(g \colon x \mapsto \ln{[f(x)]}\)


