Betrachtet wird für jeden Wert \(c \in \mathbb R^+\) das Rechteck mit den Eckpunkten \(P(-c|0)\), \(Q(c|0)\), \(R(c|f(c))\) und \(S\).
Zeichnen Sie für \(c = 2\) das Rechteck \(PQRS\) in Abbildung 1 ein.
(1 BE)
Lösung zu Teilaufgabe 1c
\[f(x) = 2e^{-\frac{1}{8}x^2}; \; D_f = \mathbb R\]
Für \(\textcolor{#e9b509}{c = 2}\) gilt: \(P(-\textcolor{#e9b509}{2}|0)\), \(Q(\textcolor{#e9b509}{2}|0)\), \(R(\textcolor{#e9b509}{2}|f(\textcolor{#e9b509}{2}))\) und \(S(-\textcolor{#e9b509}{2}|f(\textcolor{#e9b509}{2}))\)
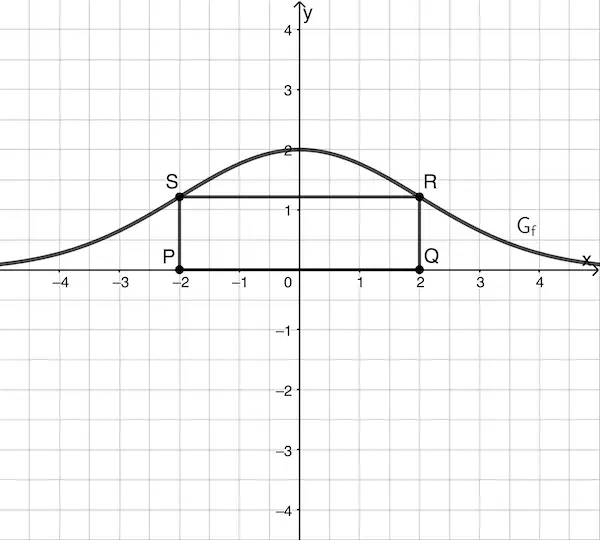 Abb. 1
Abb. 1
Rechteck \(PQRS\) für \(c = 2\)


