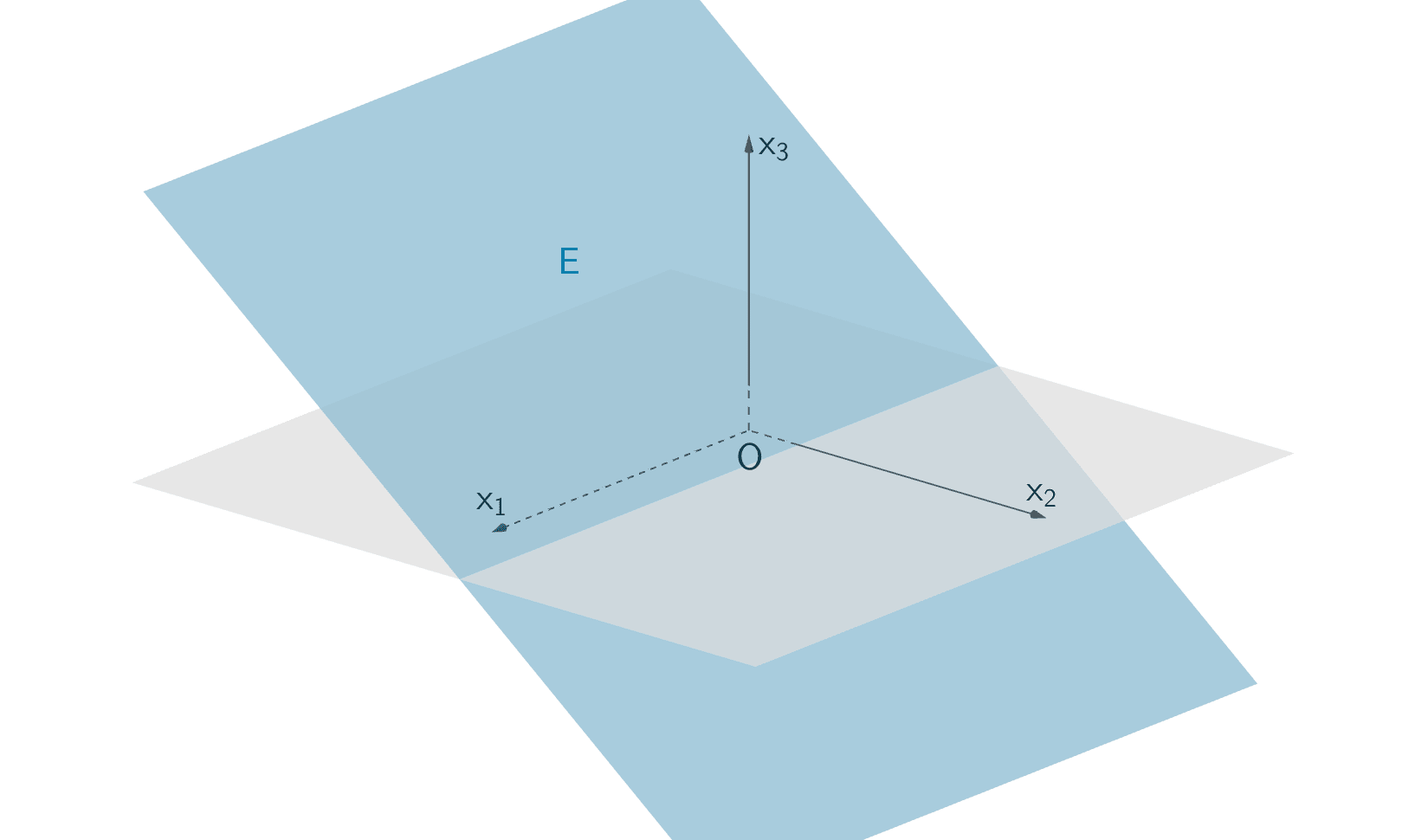
Gegeben ist die Ebene \(E\,\colon \, 3x_2 + 4x_3 = 5\).
Beschreiben Sie die besondere Lage von \(E\) im Koordinatensystem.
(1 BE)
Lösung zu Teilaufgabe 2a
\[E\,\colon \, 3x_2 + 4x_3 = 5\]
\[\Longrightarrow \quad n_{E} = \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix}\,; \quad O\,(0|0|0) \notin E\]
Die \(x_1\)-Koordinate des Normalenvektors \(n_{E}\) der Ebene \(E\) ist gleich Null. Folglich ist der Normalenvektor parallel zur \(x_2x_3\)-Ebene bzw. senkrecht zur \(x_1\)-Achse. Der Koordinatenursprung \(O\,(0|0|0)\) liegt nicht in der Ebene \(E\). Die Ebene \(E\) ist somit echt parallel zur \(x_1\)-Achse.
Lage der Ebene \(E\) im Koordinatensystem: \(E \parallel x_1\text{-Achse}\)