Gegeben ist die in \(\mathbb R^{+}\) definierte Funktion \(f \colon x \mapsto 2 \cdot \left( \left( \ln{x} \right)^{2} - 1\right)\). Abbildung 1 zeigt den Graphen \(G_{f}\) von \(f\).
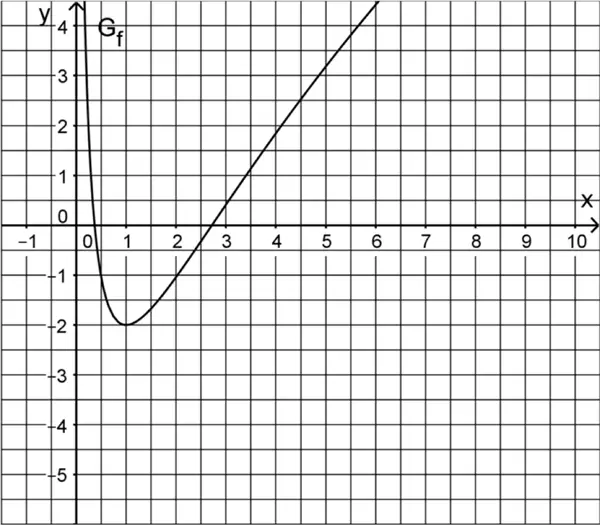 Abb. 1
Abb. 1
Zeigen Sie, dass \(x = e^{-1}\) und \(x = e\) die einzigen Nullstellen von \(f\) sind, und berechnen Sie die Koordinaten des Tiefpunkts \(T\) von \(G_{f}\).
(zur Kontrolle: \(f'(x) = \frac{4}{x} \cdot \ln{x}\))
(5 BE)
Lösung zu Teilaufgabe 1a
\[f(x) = 2 \cdot \left( \left( \ln{x} \right)^{2} - 1\right); \; D_{f} = \mathbb R^{+}\]
Nachweis der Nullstellen von \(f\)
\[\begin{align*} f(x) &= 0 \\[0.8em] 2 \cdot \left( \left( \ln{x} \right)^{2} - 1 \right) &= 0 &&| : 2 \\[0.8em] \left( \ln{x} \right)^{|2} - 1 &=0 &&| + 1 \\[0.8em] \left( \ln{x} \right)^{2} &= 1 &&| \; \sqrt{\quad} \\[0.8em] \ln{x} &= \pm 1 &&| \; e^{(\dots)}\\[0.8em] e^{\ln{x_{1}}} &= e^{1} \; \vee \; e^{\ln{x_{2}}} = e^{-1} &&| \; e^{ln{x}} = x \\[0.8em] x_{1} &= e \; \vee \; x_{2} = e^{-1} = \frac{1}{e} \end{align*}\]
Koordinaten des Tiefpunkts \(T\)
Die notwendige Bedingung für einen Extrenmpunkt von \(G_{f}\) lautet:
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[f'(x) = 0\]
Erste Ableitung \(f'\) bilden:
Hierfür wird die Kettenregel, die Ableitung einer Potenzfunktion, die Ableitung der Natürlichen Logarithmusfunktion sowie die Summen- und die Faktorregel benötigt. Als Alternative lässt sich nach einer Umformulierung von f(x) auch die Produktregel anwenden.
\[\begin{align*}f(x) &= 2 \cdot \left( \left( \ln{x} \right)^{2} - 1\right) \\[0.8em] &= 2\left( \ln{x} \right)^{2} - 2 \\[0.8em] &= 2 \cdot \ln{x} \cdot \ln{x} - 2\end{align*}\]
1. Möglichkeit: Kettenregel anwenden
\[\begin{align*}f(x) &= 2 \cdot \left( \left( \ln{x} \right)^{2} - 1\right) \\[0.8em] &= 2\textcolor{#0087c1}{(} \textcolor{#cc071e}{\ln{x}} \textcolor{#0087c1}{)^{2}} - 2\end{align*}\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
\[f'(x) = 2 \cdot \textcolor{#0087c1}{2 \cdot (} \textcolor{#cc071e}{\ln{x}} \textcolor{#0087c1}{)^{1}} \cdot \textcolor{#cc071e}{\frac{1}{x}} - 0 = \frac{4}{x} \cdot \ln{x}\]
2. Möglichkeit: Produktregel anwenden
\[\begin{align*}f(x) &= 2 \cdot \left( \left( \ln{x} \right)^{2} - 1\right) \\[0.8em] &= 2 \cdot \textcolor{#0087c1}{\ln{x}} \cdot \textcolor{#cc071e}{\ln{x}} - 2\end{align*}\]
\[\begin{align*} f'(x) &= 2 \cdot \textcolor{#0087c1}{\frac{1}{x}} \cdot \textcolor{#cc071e}{\ln{x}} + \textcolor{#0087c1}{\ln{x}} \cdot \textcolor{#cc071e}{\frac{1}{x}} - 0 \\[0.8em] &= 2 \cdot 2 \cdot \frac{1}{x} \cdot \ln{x} \\[0.8em] &= \frac{4}{x} \cdot \ln{x} \end{align*}\]
Nullstelle von \(f'(x)\) bestimmen:
\[\begin{align*} f'(x) &= 0 \\[0.8em] \frac{4}{x} \cdot \ln{x} &= 0 &&| \cdot x \\[0.8em] 4 \cdot \ln{x} &= 0 &&| : 4 \\[0.8em] \ln{x} &= 0 &&| \; e^{(\dots)} \\[0.8em] e^{\ln{x}} &= e^{0} &&| \; e^{ln{x}} = x; \; e^{0} = 1 \\[0.8em] x &= 1 \end{align*}\]
Alternative: Nach dem Satz vom Nullprodukt ist ein Produkt genau dann gleich Null. wenn einer der Faktoren gleich Null ist.
\[\begin{align*} f'(x) &= 0 \\[0.8em] \underbrace{\frac{4}{x}}_{\Large{\neq\,0}} \cdot \ln{x} &= 0 \\[0.8em] \Longrightarrow \quad ln{x} &= 0 &&| \; e^{(\dots)} \\[0.8em] e^{\ln{x}} &= e^{0} &&| \; e^{ln{x}} = x; \; e^{0} = 1 \\[0.8em] x &= 1 \end{align*}\]
\(x = 1\) ist einzige Nullstelle von \(f'\) und damit einzige mögliche Extremstelle (vgl. \(x\)-Koordinate des Tiefpunkts von \(G_{f}\) in Abb. 1 der Angabe).
Da \(G_{f}\) laut Angabe einen Tiefpunkt \(T\) besitzt, hat dieser die Koordinaten \(T(1|f(1))\).
Anmerkung:
Oft wird bei dieser Art von Aufgabe nach „Art und Lage des Extrempunkts" gefragt. Die Art eines Extrempunkts lässt sich mithilfe einer Monotonietabelle oder mithilfe der zweiten Ableitung ermitteln (vgl. Ergänzung). Da die Aufgabenstellung in diesem Fall vorgibt, dass der Extrempunkt ein Tiefpunkt ist, kann dieser Schritt entfallen.
\(y\)-Koordinate des Tiefpunkts \(T\) berechnen:
\[f(1) = 2 \cdot \left( \left( \ln{1} \right)^{2} - 1 \right) = 2 \cdot (0^{2} - 1) = -2\]
\(\Longrightarrow \quad T(1|-2)\) (vgl. Abb. 1)
Ergänzung (nicht verlangt!): Nachweis, dass \(G_{f}\) an der Stelle \(x = 1\) einen Tiefpunkt hat
1. Möglichkeit: Monotonietabelle
Es wird der Vorzeichenwechsel von \(f'(x)\) an der Stelle \(x = 1\) untersucht und anhand des Monotoniekriteriums das Monotonieverhalten von \(G_{f}\) betrachtet.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\(f'(x) = \dfrac{4}{x} \cdot \ln{x}\) mit \(x \in \mathbb R^{+}\)
Der Faktor \(\ln{x}\) bestimmt den Vorzeichenwechsel von \(f'(x)\) an der Stelle \(x = 1\).
Für \(0 < x < 1\) gilt \(\ln{x} < 0\) und für \(x > 1\) gilt \(\ln{x} > 0\).
| \(x\) | \(0 < x < 1\) | \(1\) | \(x > 1\) |
| \(\dfrac{4}{x}\) | \(+\) | \(+\) | \(+\) |
| \(\ln{x}\) | \(-\) | \(0\) | \(+\) |
| \(f'(x)\) | \(\textcolor{#cc071e}{\Large{-}}\) | \(0\) | \(\textcolor{#0087c1}{\Large{+}}\) |
| \(G_{f}\) | \(\textcolor{#cc071e}{\Large{\searrow}}\) | \(T(1|f(1))\) | \(\textcolor{#0087c1}{\Large{\nearrow}}\) |
2. Möglichkeit: Art eines Extrempunkts mithilfe der zweiten Ableitung nachweisen
Das Vorzeichen von \(f''(1)\) bestimmt das Krümmungsverhalten von \(G_{f}\) an der Stelle \(x = 1\) und lässt damit auf die Art des Extrempunkts schließen.
Die zweite Ableitung \(f''\) kann mithilfe der Quotientenregel gebildet werden.
\[f'(x) = \frac{4}{x} \cdot \ln{x} = 4 \cdot \frac{\textcolor{#0087c1}{\ln{x}}}{\textcolor{#cc071e}{x}}\]
\[\begin{align*} f''(x) &= 4 \cdot \left( \frac{\textcolor{#0087c1}{\frac{1}{x}} \cdot \textcolor{#cc071e}{x} - \textcolor{#0087c1}{\ln{x}} \cdot \textcolor{#cc071e}{1}}{\textcolor{#cc071e}{x^{2}}} \right) \\[0.8em] &= 4 \cdot \left( \frac{1 - \ln{x}}{x^{2}} \right) \\[0.8em] &= \frac{4}{x^{2}} \cdot (1 - \ln{x}) \end{align*}\]
\[f''(1) = \frac{4}{1^{2}} \cdot (1 - \ln{1}) = 4 \cdot (1 - 0) = 4 \quad \Longrightarrow \quad f''(1) > 0\]
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
Mit \(f''(1) > 0\) ist \(G_{f}\) an der Stelle \(x = 1\) linksgekrümmt \((\style{display: inline-block; transform:rotate(0.5turn);}{\Large \curvearrowleft})\). Somit besitzt \(G_{f}\) an der Stelle \(x = 1\) den Tiefpunkt \(T(1|f(1))\).


