Durch die in Aufgabe 2 entstandene herzförmige Figur soll das abgebildete Blatt modellhaft beschrieben werden. Eine Längeneinheit in Koordinatensystem aus Aufgabe 1d soll dabei 1 cm in Wirklichkeit entsprechen.
Berechnen Sie den Inhalt des von \(G_h\) und der Winkelhalbierenden \(w\) eingeschlossenen Flächenstücks. Bestimmen Sie unter Verwendung dieses Werts den Flächeninhalt des Blatts auf der Grundlage des Modells.

(5 BE)
Lösung zu Teilaufgabe 3a
Inhalt des von \(G_h\) und der Winkelhalbierenden \(w\) eingeschlossenen Flächenstücks
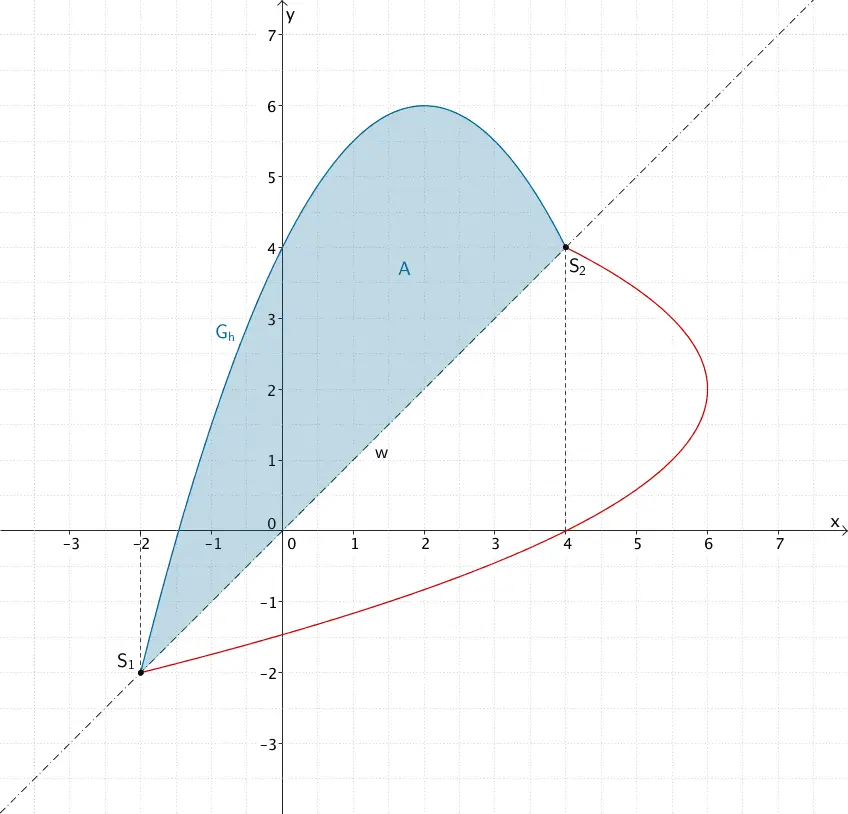
Von \(G_{h}\) und der Winkelhalbierenden \(w\) eingeschlossenes Flächenstück
\[h(x) = -\frac{1}{2}x^2 + 2x + 4\]
\[w(x) = x\]
Das bestimmte Integral \(\displaystyle \int_{-2}^{4} (h(x) - w(x))\,dx\) errechnet den Flächeninhalt \(A\) des von \(G_{h}\) und der Winkelhalbierenden \(w\) eingeschlossenen Flächenstücks.
\[A = \int_{-2}^{4} (h(x) - w(x))\,dx\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[h(x) - w(x) = -\frac{1}{2}x^2 +2x + 4 - x = -\frac{1}{2}x^2 + x + 4\]
Stammfunktion einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad F(x) = \frac{1}{r + 1} \cdot x^{r + 1} + C\]
\[r \neq -1\]
\[\begin{align*} A &= \int_{-2}^{4}\left( -\frac{1}{2}x^2 + x + 4 \right)dx \\[0.8em] &= \left[ -\frac{1}{6}x^3 + \frac{1}{2}x^2 + 4x \right]_{-2}^{4} \\[0.8em] &= -\frac{1}{6} \cdot 4^3 + \frac{1}{2} \cdot 4^2 + 4 \cdot 4 - \left( -\frac{1}{6} \cdot (-2)^3 + \frac{1}{2} \cdot (-2)^2 + 4 \cdot (-2) \right) \\[0.8em] &= -\frac{32}{3} + 8 + 16 - \left( \frac{4}{3} + 2 - 8 \right) \\[0.8em] &= 13\frac{1}{3} - \left( -4\frac{2}{3} \right) \\[0.8em] &= 18 \end{align*}\]
Der Flächeninhalt des von \(G_{h}\) und der Winkelhalbierenden \(w\) eingeschlossenen Flächenstücks beträgt 18 FE (Flächeneinheit).
Flächeninhalt des Blatts auf der Grundlage des Modells
Der Flächeninhalt des Blatts auf der Grundlage des Modells ist gleich dem doppelten Flächeninhalt \(A\) des von \(G_{h}\) und der Winkelhalbierenden \(w\) eingeschlossenen Flächenstücks. Dabei entspricht eine Flächeneinheit (FE) einem Quadratzentimeter des Blatts.
\[A_{\text{Blatt}} = 2 \cdot A = (2 \cdot 18)\;\text{cm}^2 = 36\;\text{cm}^2\]


