Für einen bestimmten Wert \(n \in \{1;2;3;\dots\}\) werden für \(p \in \;]0;1[\) die binomialverteilten Zufallsgrößen \(Z_p\) mit den Parametern \(n\) und \(p\) betrachtet. Weisen Sie nach, dass unter diesen Zufallsgrößen diejenige mit \(p = 0{,}5\) die größte Varianz hat.
(3 BE)
Lösung zu Teilaufgabe 1d
Nach \(B(n;p)\) binomialverteilte Zufallsgröße \(Z_p\)
Erwartungswert \(\boldsymbol{\mu}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\(\mu = E(X) = n \cdot p\) (vgl. Merkhilfe)
Varianz \(\boldsymbol{Var(X)}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\):
\(Var(X) = n \cdot p \cdot (1 - p)\) (vgl. Merkhilfe)
Standardabweichung \(\boldsymbol{\sigma}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\[\sigma = \sqrt{Var(X)} = \sqrt{n \cdot p \cdot (1 - p)}\]
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist.
\[Var(Z_p) = n \cdot p \cdot (1 - p)\]
1. Möglichkeit: halbgraphischer Nachweis
\[Var(Z_p) = n \cdot \textcolor{#cc071e}{p \cdot (1 - p)} = n \cdot \textcolor{#cc071e}{(p - p^2)} = n \cdot \textcolor{#cc071e}{(-p^2 + p)}\]
Der Term \(\textcolor{#cc071e}{p \cdot (1 - p)}\) lässt sich graphisch als nach unten geöffnete Parabel mit den Nullstellen \(0\) und \(1\) interpretieren. Der Scheitelpunkt (Hochpunkt) der Parabel liegt mittig zwischen den Nullstellen auf der Symmetrieachse mit der Gleichung \(p = 0{,}5\).
Somit hat unter den Zufallsgrößen \(Z_p\) diejenige mit \(p = 0{,}5\) die größte Varianz.
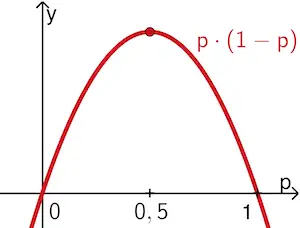(Skizze optional)
2. Möglichkeit: Differentialrechnung anwenden
\(Var(Z_p)\) nach \(p\) ableiten:
\[Var(Z_p) = n \cdot p \cdot (1 - p) = n \cdot (-p^2 + p)\]
Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[\begin{align*}Var'(Z_p) &= [n \cdot (-p^2 + p)]' \\[0.8em] &= n \cdot (-2p + 1) \\[0.8em] &= n \cdot (-2) \cdot (p - 0{,}5)\end{align*}\]
Notwendige Bedingung für ein Maximum von \(Var(Z_p)\) formulieren:
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[Var'(Z_p) = 0 \; \Rightarrow \; p - 0{,}5 = 0 \; \Rightarrow \; p = 0{,}5\]
Maximum mithilfe der zweiten Ableitung nachweisen:
\[Var'(Z_p) = n \cdot (-2p + 1)\]
\[Var''(Z_p) = [n \cdot (-2p + 1)]' = -2n\]
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
Mit \(n \in \{1;2;3;\dots\}\) (vgl. Angabe) folgt \(Var''(Z_p) = -2n < 0\). Also hat unter den Zufallsgrößen \(Z_p\) diejenige mit \(p = 0{,}5\) die größte Varianz.
Oder Maximum durch geeigneten Vorzeichenwechsel (VZW) von \(Var'(Z_p)\) nachweisen:
\[Var'(Z_p) = n \cdot (-2p + 1) = \underbrace{n \cdot (-2)}_{<\,0} \cdot \textcolor{#e9b509}{\underbrace{(p - 0{,}5)}_{\text{VZW}}}\]
\[\left. \begin{align*} &Var'(Z_p) \textcolor{#0087c1}{> 0} \; \text{für} \; p < 0{,}5 \\ &Var'(Z_p) = 0 \; \text{für} \; p = 0{,}5 \\ &Var'(Z_p) \textcolor{#cc071e}{< 0} \; \text{für} \; p > 0{,}5 \end{align*} \right \} \Rightarrow Var(Z_p) \;\text{ist für}\;p = 0{,}5\;\text{maximal.}\]
Veranschaulichung mithilfe einer Monotonietabelle:
| \(p\) | \(]0;0{,}5[\) | \(0{,}5\) | \(]0{,}5;1[\) |
| \(\textcolor{#e9b509}{(p - 0{,}5)}\) | \(\textcolor{#cc071e}{–}\) | \(\textcolor{#0087c1}{+}\) | |
| \(Var'(Z_p)\) | \(\textcolor{#0087c1}{+}\) | \(0\) | \(\textcolor{#cc071e}{–}\) |
| \(G_{Var(Z_p)}\) | \(\textcolor{#0087c1}{\nearrow}\) | \(\text{Max.}\) | \(\textcolor{#cc071e}{\searrow}\) |
