Der JIM-Studie zufolge besitzen deutlich weniger als 90 % der Jugendlichen einen Computer. Daher wird an den Stadtrat einer Kleinstadt der Wunsch herangetragen, im örtlichen Jugendzentrum einen Arbeitsraum mit Computern einzurichten. Der Stadtrat möchte die dafür erforderlichen finanziellen Mittel nur dann bewilligen, wenn weniger als 90 % der Jugendlichen der Kleinstadt einen Computer besitzen.
Die Entscheidung über die Bewilligung der finanziellen Mittel soll mithilfe einer Befragung von 100 zufällig ausgewählten 12- bis 19-jährigen Jugendlichen der Kleinstadt getroffen werden. Die Wahrscheinlichkeit dafür, dass die finanziellen Mittel irrtümlich bewilligt werden, soll höchstens 5 % betragen. Bestimmen Sie die zugehörige Entscheidungsregel, bei der zugleich die Wahrscheinlichkeit dafür, dass die finanziellen Mittel irrtümlich nicht bewilligt werden, möglichst klein ist.
(4 BE)
Lösung zu Teilaufgabe 2a
Signifikanztest
Zufallsgröße \(X\,\colon\enspace\)„Anzahl der 12- bis 19-jährigen Jugendlichen der Kleinstadt, die einen Computer besitzen"
Analyse der Angabe:
„... mithilfe einer Befragung von 100 zufällig ausgewählten 12- bis 19-jährigen Jugendlichen der Kleinstadt..."
\[\Longrightarrow \quad n = 100\]
„Die Wahrscheinlichkeit dafür, dass die finanziellen Mittel irrtümlich bewilligt werden, soll höchstens 5 % betragen."
\(\Longrightarrow \quad\) Signifikanzniveau: \(\alpha = 0{,}05\)
Da die Entscheidung über die Annahme oder Ablehnung einer Nullhypothese aufgrund eines zufälligen Ergebnisses einer Stichprobe erfolgt, kann es zu Fehlentscheidungen kommen.
Fehler 1. Art und Fehler 2. Art
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Fehler 2. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich angenommen bzw. nicht abgelehnt.
(vgl. Merkhilfe)
| \(H_{0}\) ist wahr | \(H_{0}\) ist falsch | |
| \(H_{0}\) wird abgelehnt | Fehler 1. Art | richtige Entscheidung |
| \(H_{0}\) wird nicht abgelehnt | richtige Entscheidung | Fehler 2. Art |
Wahrscheinlichkeit \(\boldsymbol{\alpha'}\) für den Fehler 1. Art
\[\alpha' = P(\text{Fehler 1. Art}) = P^{n}_{p_0} (X \in \overline{A})\]
Wahrscheinlichkeit \(\boldsymbol{\beta'}\) für den Fehler 2. Art
\[\beta' = P(\text{Fehler 2. Art}) = P^n_{p_{1}} (X \in A)\]
Wobei \(A\) der Annahmebereich und \(\overline{A}\) der Ablehnungsbereich der Nullhypothese \(H_0\) ist. \(H_{1}\) bezeichnet die Gegenhypothese.
\(\Longrightarrow \quad P(\text{„Fehler 1. Art"}) \leq 0{,}05\)
„Der Stadtrat möchte die erforderlichen finanziellen Mittel nur dann bewilligen, wenn weniger als 90 % der Jugendlichen der Kleinstadt einen Computer besitzen."
\(\Longrightarrow \quad\) Nullhypothese \(H_{0} \,\colon \, p_{0} = 0{,}9\)
Die Wahl der Nullhypothese ist eine Frage der Interessensperspektive. Beim Signifikanztest hängt sie davon ab, welchen sachbezogenen Irrtum der Fehler 1. Art beschreiben soll. Im vorliegenden Fall sollen nicht irrtümlich finanzielle Mittel bewilligt werden. Dies ist dann der Fall, wenn tatsächlich 90 % der 12- bis 19-jährigen Jugendlichen der Kleinstadt einen Computer besitzen, von den befragten Jugendlichen aber nur wenige angeben, einen Computer zu besitzen. Die Irrtumswahrscheinlichkeit dafür soll höchstens 5 % betragen. Da der Signifikanztest per Definition dem Fehler 1. Art eine Obergrenze setzt (Signifikanzniveau) und der Fehler 1. Art bedeutet, dass die Nullhypothese irrtümlich abgelehnt wird, muss die Nullhypothese im Sachzusammenhang lauten: „90 % der 12- 19-jährigen Jugendlichen der Kleinstadt besitzen einen Computer."
„Bestimmen Sie die zugehörige Entscheidungsregel, bei der zugleich die Wahrscheinlichkeit dafür, dass die finanziellen Mittel irrtümlich nicht bewilligt werden, möglichst klein ist.
Da die Entscheidung über die Annahme oder Ablehnung einer Nullhypothese aufgrund eines zufälligen Ergebnisses einer Stichprobe erfolgt, kann es zu Fehlentscheidungen kommen.
Fehler 1. Art und Fehler 2. Art
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Fehler 2. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich angenommen bzw. nicht abgelehnt.
(vgl. Merkhilfe)
| \(H_{0}\) ist wahr | \(H_{0}\) ist falsch | |
| \(H_{0}\) wird abgelehnt | Fehler 1. Art | richtige Entscheidung |
| \(H_{0}\) wird nicht abgelehnt | richtige Entscheidung | Fehler 2. Art |
Wahrscheinlichkeit \(\boldsymbol{\alpha'}\) für den Fehler 1. Art
\[\alpha' = P(\text{Fehler 1. Art}) = P^{n}_{p_0} (X \in \overline{A})\]
Wahrscheinlichkeit \(\boldsymbol{\beta'}\) für den Fehler 2. Art
\[\beta' = P(\text{Fehler 2. Art}) = P^n_{p_{1}} (X \in A)\]
Wobei \(A\) der Annahmebereich und \(\overline{A}\) der Ablehnungsbereich der Nullhypothese \(H_0\) ist. \(H_{1}\) bezeichnet die Gegenhypothese.
\(\Longrightarrow \quad P(\text{„Fehler 2. Art"})\) soll möglichst klein sein
Die finanziellen Mittel werden irrtümlich nicht bewilligt, wenn weniger als 90 % der 12- bis 19-jährigen der Kleinstadt einen Computer besitzen, von den befragten Jugendlichen aber viele angeben, einen Computer zu besitzen. Also wenn die Gegenhypothese \(H_{1}\,\colon\,p < 0{,}9\) zutrifft, das Ergebnis der Befragung aber im Annahmebereich \(A\) der Nullhypothese \(H_{0}\,\colon\,p_{0} = 0{,}9\) liegt. Die Irrtumswahrscheinlichkeit für den Fehler 2. Art \(P_{p_1}^{100}(X \in A)\) ist umso kleiner, je kleiner der Annahmebereich \(A\) der Nullhypothese \(H_{0}\) ist bzw. je größer der Ablehnungsbereich \(\overline{A}\) der Nullhypothese \(H_{0}\) ist.
Linksseitiger Signifikanztest
Einseitiger Signifikanztest zum Signifikanzniveau \(\boldsymbol{\alpha}\)
Ein einseitiger Signifikanztest zum Signifikanzniveau \(\alpha\) überprüft eine Vermutung, dass eine Wahrscheinlichkeit \(p\) größer bzw. kleiner als eine bestimmte Wahrscheinlichkeit \(p_{0}\) ist. Dabei darf die Wahrscheinlichkeit für den Fehler 1. Art höchstens den Wert des Signifikanzniveaus \(\alpha\) erreichen.
Linksseitiger Signifikanztest
\[H_0 \colon p_0 \geq p \quad H_1 \colon p_1 < p\]
Ablehnungsbereich von \(H_0\):
\[\overline{A} = \{0; 1; ...; k\}\]
Bedingung für den Fehler 1. Art:
\[\begin{align*} P_{p_{0}}^{n}(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \leq k) &\leq \alpha \\[1.6em] \overset{\text{ST}}{\Longrightarrow} \enspace k \enspace \Longrightarrow \enspace A, \overline{A} \end{align*}\]
Rechtsseitiger Signifikanztest
\[H_0 \colon p_0 \leq p \quad H_1 \colon p_1 > p\]
Ablehnungsbereich von \(H_0\):
\[\overline{A} = \{k + 1; ...; n\}\]
Bedingung für den Fehler 1. Art:
\[\begin{align*} P_{p_{0}}^{n}(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \geq k +1) &\leq \alpha \\[0.8em] 1 - P_{p_{0}}^{n}(X \leq k) &\leq \alpha & &| - 1 \\[0.8em] - P_{p_{0}}^{n}(X \leq k) &\leq \alpha - 1 &&| \textcolor{red}{\cdot (-1)} \\[0.8em] P_{p_{0}}^{n}(X \leq k) &\textcolor{red}{\geq} 1 - \alpha \\[1.6em] \overset{\text{ST}}{\Longrightarrow} \enspace k \enspace \Longrightarrow \enspace A, \overline{A} \end{align*}\]
ST: Stochastisches Tafelwerk
Nullhypothese: \(H_{0}\,\colon\,p_{0} = 0{,}9\)
Gegenhypothese: \(H_{1}\,\colon\,p < 0{,}9\)
Annahmebereich von \(H_{0}\): \(A = \{k + 1; \dots ; 100\}\)
Ablehnungsbereich von \(H_{0}\): \(\overline{A} = \{0; 1; \dots ; k\}\)
Signifikanztest formulieren:
Da die Entscheidung über die Annahme oder Ablehnung einer Nullhypothese aufgrund eines zufälligen Ergebnisses einer Stichprobe erfolgt, kann es zu Fehlentscheidungen kommen.
Fehler 1. Art und Fehler 2. Art
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Fehler 2. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich angenommen bzw. nicht abgelehnt.
(vgl. Merkhilfe)
| \(H_{0}\) ist wahr | \(H_{0}\) ist falsch | |
| \(H_{0}\) wird abgelehnt | Fehler 1. Art | richtige Entscheidung |
| \(H_{0}\) wird nicht abgelehnt | richtige Entscheidung | Fehler 2. Art |
Wahrscheinlichkeit \(\boldsymbol{\alpha'}\) für den Fehler 1. Art
\[\alpha' = P(\text{Fehler 1. Art}) = P^{n}_{p_0} (X \in \overline{A})\]
Wahrscheinlichkeit \(\boldsymbol{\beta'}\) für den Fehler 2. Art
\[\beta' = P(\text{Fehler 2. Art}) = P^n_{p_{1}} (X \in A)\]
Wobei \(A\) der Annahmebereich und \(\overline{A}\) der Ablehnungsbereich der Nullhypothese \(H_0\) ist. \(H_{1}\) bezeichnet die Gegenhypothese.
\[\begin{align*} P(\text{„Fehler 1. Art"}) &\leq 0{,}05 \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq 0{,}05 \\[0.8em] P_{0{,}9}^{100}(X \leq k) &\leq 0{,}05 \end{align*}\]
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
Stochastisches Tafelwerk (ST) verwenden:
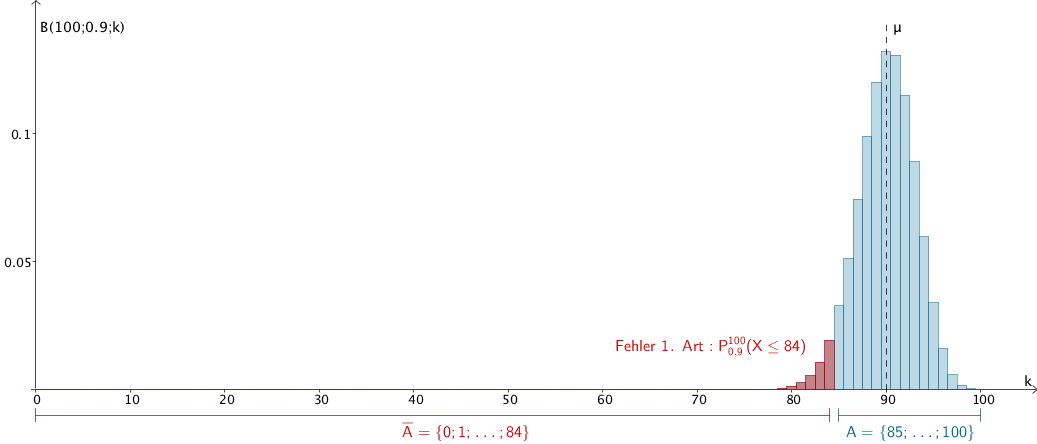
\[P_{0{,}9}^{100}(X \leq k) = F_{0{,}9}^{100}(k) = \sum \limits_{i\,=\,0}^{k} B(100;0{,}9;i) \leq 0{,}05\]
\[\overset{\text{ST}}{\Longrightarrow} \quad k \leq 84 \quad \bigg( F_{0{,}9}^{100}(84) \enspace \overset{\text{ST}}{=} \enspace 0{,}03989 \bigg)\]
Damit die Irrtumswahrscheinlichkeit für den Fehler 2. Art \(P_{p_{1}}^{100}(X \in A)\) möglichst klein ist, wählt mann \(k = 84\), denn dann ist der Annahmebereich der Nullhypothese \(H_{0}\) am kleinsten.
Entscheidungsregel formulieren:
Annahmebereich von \(H_{0}\): \(A = \{85; \dots ; 100\}\)
Ablehnungsbereich von \(H_{0}\): \(\overline{A} = \{0; 1; \dots ; 84\}\)
Wenn mehr als 84 der 100 befragten 12- bis 19-jährigen Jugendlichen der Kleinstadt angeben, einen Computer zu besitzen, werden die finanziellen Mittel für einen Arbeitsraum mit Computern im Jugendzentrum nicht bewilligt.
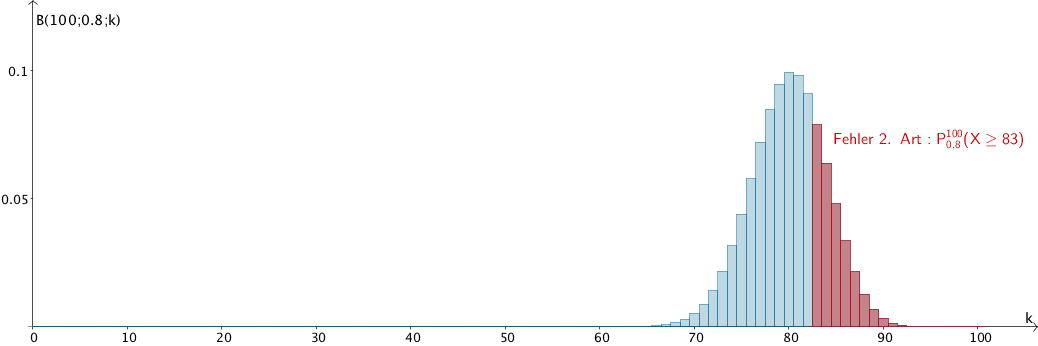
Nachfolgende Abbildungen sollen abschließend veranschaulichen, wie sich die Irrtumswahrscheinlichkeit für den Fehler 1. Art und der Fehler 2. Art verändert, wenn beispielsweise \(k = 82\) gewählt wird. Für die Berechnung des Fehlers 2. Art sei angenommen, dass nur 80 % der 12- bis 19-jährigen Jugendlichen der Kleinstadt einen Computer besitzen (\(H_{1}\,\colon\,p_{1} = 0{,}8\)).
Fehler 1. Art für \(k = 84\,\): \(P_{0{,}9}^{100}(X \leq 84) = 0{,}03989 \approx 3{,}99\,\%\)
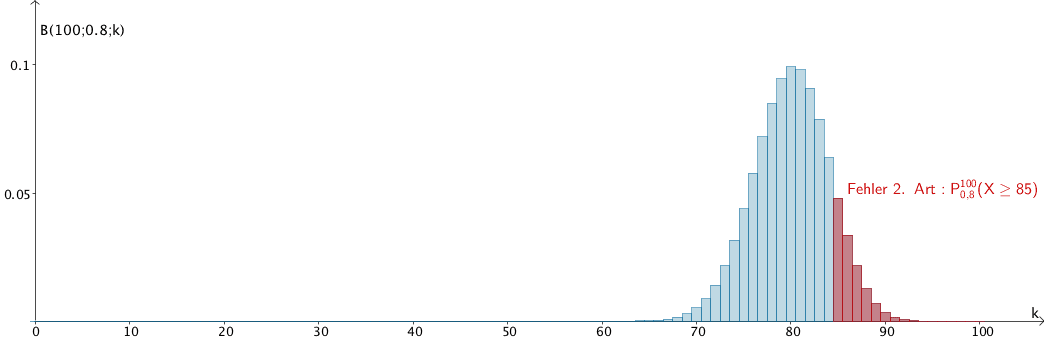
Fehler 2. Art für \(k = 84\) und \(p_{1} = 0{,}8\,\):
\[P_{0{,}8}^{100}(X \geq 85) = 1 - P_{0{,}8}^{100}(x \leq 84) = 1 - 0{,}87149 = 0{,}12851 \approx 12{,}85\,\%\]
Fehler 1. Art für \(k = 82\,\): \(P_{0{,}9}^{100}(X \leq 82) = 0{,}01001 \approx 1{,}00\,\%\)
Fehler 2. Art für \(k = 82\) und \(p_{1} = 0{,}8\,\):
\[P_{0{,}8}^{100}(X \geq 83) = 1 - P_{0{,}8}^{100}(x \leq 82) = 1 - 0{,}72881 = 0{,}27119 \approx 27{,}12\,\%\]