Bestimmen Sie rechnerisch Lage und Art des Extrempunkts von \(G_{f}\).
(5 BE)
Lösung zu Teilaufgabe b
\[f(x) = \frac{4x}{(x + 1)^{2}}; \; D_{f} = \mathbb R \backslash \{-1\}\]
Lage des Extrempunkts von \(G_{f}\)
Die notwendige Bedingung für einen Extrempunkt von \(G_{f}\) lautet:
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[f'(x) = 0\]
Erste Ableitung \(f'\) bilden:
Die Ableitungsfunktion \(f'(x)\) kann mithilfe der Quotientenregel, der Kettenregel sowie der Ableitung einer Potenzfunktion gebildet werden.
\[f(x) = \frac{\textcolor{#0087c1}{4x}}{\textcolor{#cc071e}{(x + 1)^{2}}}\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
\[\begin{align*} f'(x) &= \frac{\textcolor{#0087c1}{4} \cdot \textcolor{#cc071e}{(x + 1)^{2}} - \textcolor{#0087c1}{4x} \cdot \overbrace{\textcolor{#cc071e}{2 \cdot (x + 1) \cdot 1}}^{\large{\text{Kettenregel}}}}{\textcolor{#cc071e}{\left[ (x + 1)^{2} \right]^{2}}} \\[0.8em] &= \frac{4 \cdot (x + 1)^{2} - 8x \cdot (x + 1)}{(x + 1)^{4}} &&| \; (x + 1) \; \text{ausklammern und kürzen} \; (x \neq -1) \\[0.8em] &= \frac{\cancel{(x + 1)} \cdot [4 \cdot (x + 1) - 8x]}{(x + 1)^{\cancelto{3}{4}}} \\[0.8em] &= \frac{4x + 4 - 8x}{(x + 1)^{3}} \\[0.8em] &= \frac{4 - 4x}{(x + 1)^{3}} \\[0.8em] &= \frac{4 \cdot (1 - x)}{(x + 1)^{3}} \end{align*}\]
Nullstelle von \(f'\) berechnen:
Ein Quotient ist gleich Null, wenn der Zähler gleich Null ist.
\[f'(x) = 0 \quad \Longrightarrow \quad 4 \cdot (1 - x) = 0 \quad \Longrightarrow \quad x = 1\]
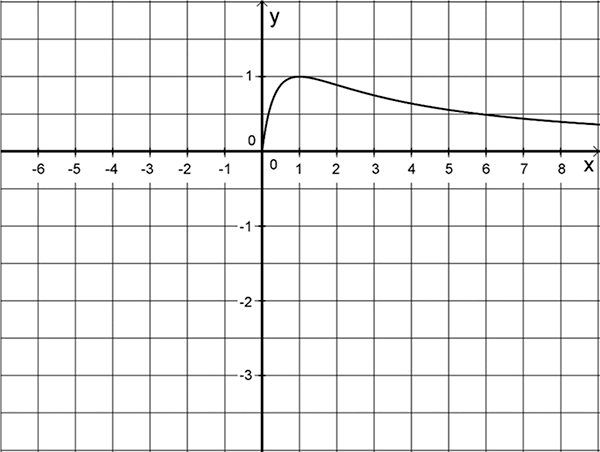
Die Abbildung bestätigt die Extremstelle \(x = 1\) von \(G_{f}\).
\(y\)-Koordinate des Extrempunkts berechnen:
\[f(1) = \frac{4 \cdot 1}{(1 + 1)^{2}} = 1\]
Somit besitzt \(G_{f}\) den Extrempunkt \((1|1)\)
Art des Extrempunkts von \(G_{f}\)
Die Abbildung (vgl. oben) zeigt den Hochpunkt \((1|1)\).
1. Möglichkeit: Monotonietabelle
Es wird der Vorzeichenwechsel von \(f'(x)\) an der Stelle \(x = 1\) untersucht und anhand des Monotoniekriteriums das Monotonieverhalten von \(G_{f}\) betrachtet.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[f'(x) = \frac{4 \cdot (1 - x)}{(x + 1)^{2}}\]
| \(x\) | \(-1 < x < 1\) | \(1\) | \(x > 1\) |
| \(f'(x)\) | \(\textcolor{#0087c1}{\Large{+}}\) | \(0\) | \(\textcolor{#cc071e}{\Large{-}}\) |
| \(G_{f}\) | \(\textcolor{#0087c1}{\Large{\nearrow}}\) | \(HoP(1|1)\) | \(\textcolor{#cc071e}{\Large{\searrow}}\) |
Testwerte z.B.: \(x = 0\) und \(x = 2\)
\[f'(0) = \frac{4 \cdot (1 - 0)}{(0 + 1)^{2}} = 4 \textcolor{#0087c1}{> 0}\]
\[f'(2) = \frac{4 \cdot (1 - 2)}{(2 + 1)^{2}} = -\frac{4}{9} \textcolor{#cc071e}{< 0}\]
Wie die Abbildung (vgl. oben) bestätigt, besitzt \(G_{f}\) den Hochpunkt \(HoP(1|1)\).
2. Möglichkeit: Art des Extrempunkts mithilfe der zweiten Ableitung nachweisen
Diese Möglichkeit sei der Vollständigkeit halber aufgeführt. Sie ist zeitaufwendiger und daher nicht zu empfehlen.
Das Vorzeichen von \(f''(1)\) bestimmt das Krümmungsverhalten von \(G_{f}\) an der Stelle \(x = 1\) und lässt damit auf die Art des Extrempunkts schließen.
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
\[f'(x) = \frac{\textcolor{#0087c1}{4 - 4x}}{\textcolor{#cc071e}{(x + 1)^{3}}}\]
\[\begin{align*} f''(x) &= \frac{\textcolor{#0087c1}{(0 - 4)} \cdot \textcolor{#cc071e}{(x + 1)^{3}} - \textcolor{#0087c1}{(4 - 4x)} \cdot \textcolor{#cc071e}{3 \cdot (x + 1)^{2} \cdot 1}}{\textcolor{#cc071e}{\left[ (x + 1)^{3} \right]^{2}}} \\[0.8em] &= \frac{(-4) \cdot (x + 1)^{3} - (12 - 12x) \cdot (x + 1)^{2}}{(x + 1)^{6}} \\[0.8em] &= \frac{\cancel{(x + 1)^{2}} \cdot \left[ (-4) \cdot (x + 1) - (12 - 12x) \right]}{(x + 1)^{\cancelto{4}{6}}} &&| \; (x \neq -1) \\[0.8em] &= \frac{-4x - 4 - 12 + 12x}{(x + 1)^{4}} \\[0.8em] &= \frac{8x - 16}{(x + 1)^{4}} \\[0.8em] &= \frac{8 \cdot (x - 2)}{(x + 1)^{4}} \end{align*}\]
\[\textcolor{#89ba17}{f''(1)} = \frac{8 \cdot (1 - 2)}{(1 + 1)^{2}} = \frac{-8}{16} = -\frac{1}{2} \textcolor{#89ba17}{< 0} \quad \Longrightarrow \quad \textcolor{#89ba17}{HoP(1|1)}\]


