Abiturlösungen Mathematik Bayern 2023 Prüfungsteil B Analysis 1

Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto 2e^{-\frac{1}{8}x^2}\). Abbildung 1 zeigt den Graphen \(G_f\) von \(f\), der die \(x\)-Achse als waagrechte Asymptote besitzt.

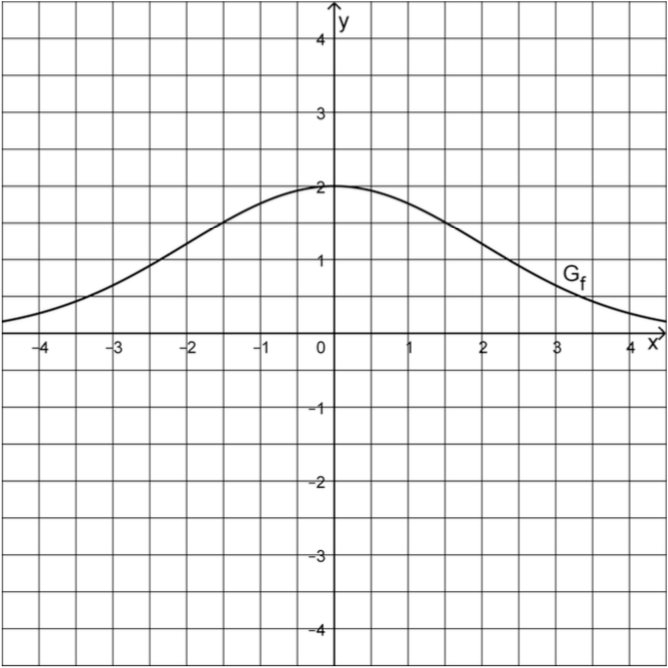Abb. 1

Berechnen Sie die Koordinaten des Schnittpunkts von \(G_f\) mit der \(y\)-Achse und weisen Sie rechnerisch nach, dass \(G_f\) symmetrisch bezüglich der \(y\)-Achse ist.

(2 BE) 

Der Punkt \(W\Big(-2\Big|2e^{-\frac{1}{2}}\Big)\) ist einer der beiden Wendepunkte von \(G_f\). Die Tangente an \(G_f\) im Punkt \(W\) wird mit \(w\) bezeichnet. Ermitteln Sie eine Gleichung von \(w\) und berechnen Sie die Stelle, an der \(w\) die \(x\)-Achse schneidet.

(zur Kontrolle: \(f'(x) = -\frac{1}{2}x \cdot e^{-\frac{1}{8}x^2}\,\))

(5 BE) 

Betrachtet wird für jeden Wert \(c \in \mathbb R^+\) das Rechteck mit den Eckpunkten \(P(-c|0)\), \(Q(c|0)\), \(R(c|f(c))\) und \(S\).

Zeichnen Sie für \(c = 2\) das Rechteck \(PQRS\) in Abbildung 1 ein.

(1 BE) 

Berechnen Sie denjenigen Wert von \(c\), für den \(\overline{QR} = 1\) gilt.

(3 BE) 

Geben Sie in Abhängigkeit von \(c\) die Seitenlängen des Rechtecks \(PQRS\) an und begründen Sie, dass der Flächeninhalt des Rechtecks durch den Term \(A(c) = 4c \cdot e^{-\frac{1}{8}c^2}\) gegeben ist.

(3 BE) 

Es gibt einen Wert von \(c\), für den der Flächeninhalt \(A(c)\) des Rechtecks \(PQRS\) maximal ist. Berechnen Sie diesen Wert von \(c\).

(4 BE) 

Betrachtet werden für \(k \in \mathbb R\) die in \(]-\infty;0]\) definierten Funktionen \(f_k \colon x \mapsto f(x) + k\). Somit gilt \(f_0(x) = f(x)\), wobei sich \(f_0\) und \(f\) im Definitionsbereich unterscheiden.

Begründen Sie mithilfe der ersten Ableitung von \(\boldsymbol{f_k}\), dass \(f_k\) für jeden Wert von \(k\) umkehrbar ist. Skizzieren Sie in Abbildung 1 den Graphen der Umkehrfunktion von \(f_0\).

(4 BE) 

Geben Sie alle Werte von \(k\) an, für die der Graph von \(f_k\) und der Graph der Umkehrfunktion von \(f_k\) keinen gemeinsamen Punkt haben.

(2 BE) 

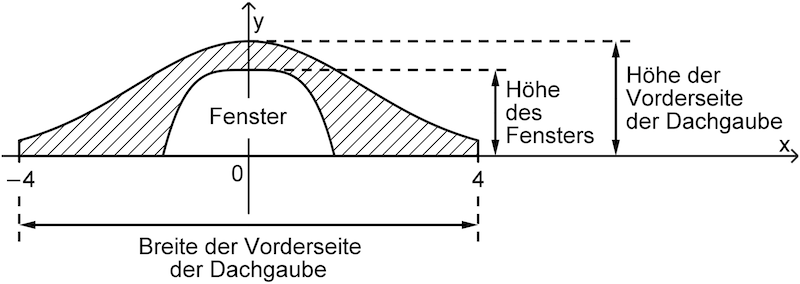Abb. 3

Geben Sie die Breite und Höhe der Vorderseite der Dachgaube an.

(2 BE) 

In der Vorderseite der Dachgaube befindet sich ein Fenster. Dem Fenster entspricht im Modell das Flächenstück, das der Graph der Funktion \(g\) mit \(g(x) = ax^4 + b\) und geeigneten Werten \(a,b \in \mathbb R\) mit der \(x\)-Achse einschließt (vgl. Abbildung 3).

Begründen Sie, dass a negativ und b positiv ist.

(2 BE) 

Um den Flächeninhalt der Vorderseite der Dachgaube zu ermitteln, wird eine Stammfunktion \(F\) von \(f\) betrachtet.

Einer der Graphen I, II und III ist der Graph von \(F\). Begründen Sie, dass dies Graph I ist, indem Sie jeweils einen Grund dafür angeben, dass Graph II und Graph III nicht infrage kommen.

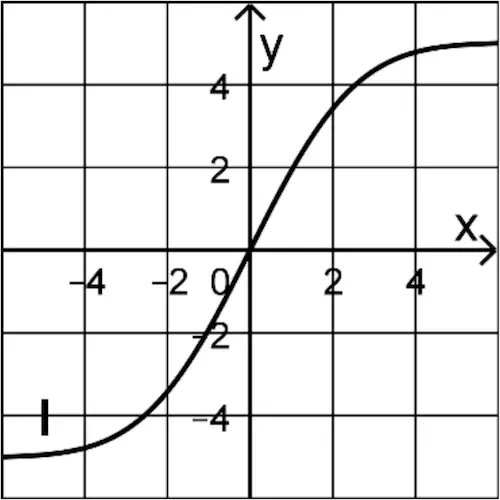
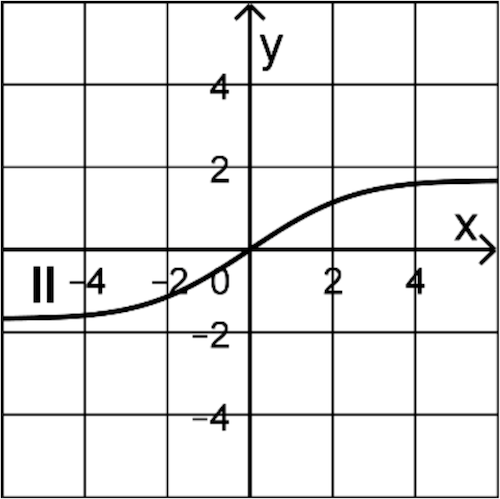
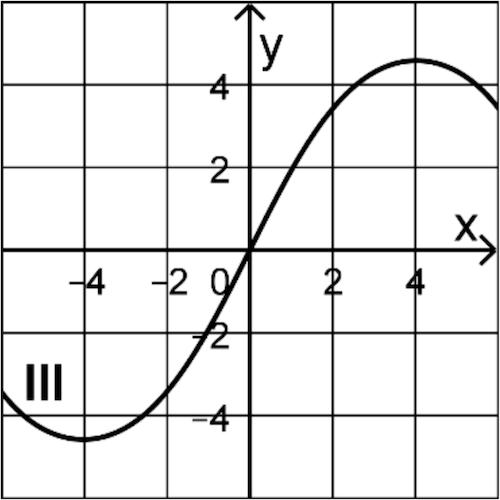
(2 BE) 

Bestimmen Sie nun mithilfe des Graphen von \(\boldsymbol{F}\) aus Aufgabe 2c den Flächeninhalt der gesamten Vorderseite der Dachgaube (einschließlich des Fensters).

Beschreiben Sie unter Einbeziehung dieses Flächeninhalts die wesentlichen Schritte eines Lösungswegs, mit dem der Wert von \(a\) rechnerisch so bestimmt werden könnte, dass bei einer Fensterhöhe von 1,50 m der Teil der Vorderseite der Dachgaube, der in Abbildung 3 schraffiert dargestellt ist, den Flächeninhalt 6 m² hat.

(5 BE) 

Um einen Näherungswert für die Länge der oberen Profillinie der Vorderseite der Dachgaube berechnen zu können, wird \(G_f\) im Bereich \(-4 \leq x \leq 4\) durch vier Kreisbögen angenähert, die nahtlos ineinander übergehen und zueinander kongruent sind. Einer dieser Kreisbögen erstreckt sich im Bereich \(0 \leq x \leq 2\) und ist Teil des Kreises mit Mittelpunkt \(M(0|-1)\) und Radius 3. Berechnen Sie den Mittelpunktswinkel des zu diesem Kreisbogen gehörenden Kreissektors und ermitteln Sie damit den gesuchten Näherungswert.

(5 BE)