Gegeben ist die gebrochenrationale Funktion \(f \colon x \mapsto \dfrac{-2x-4}{x^3+6x^2+9x}\) mit maximaler Definitionsmenge \(D_f\). Der Graph von \(f\) wird mit \(G_f\) bezeichnet.
a) Geben Sie die Nullstelle von \(f\) an. Untersuchen Sie \(f\) auf Polstellen und geben Sie \(D_f\) an. Bestimmen Sie das Verhalten von \(G_f\) an den Definitionslücken.
b) Untersuchen Sie \(G_f\) auf schräge oder waagrechte Asymptoten.
c) Berechnen Sie \(f(-4)\) und \(f(1)\) und zeichnen Sie \(G_f\) im Bereich \(-7 < x < 4\) in ein Koordinatensystem.
\[f(x) = \frac{-2x-4}{x^3+6x^2+9x}\]
a) Nullstelle von \(f\), Untersuchen von \(f\) auf Polstellen, maximale Definitionsmenge \(D_f\) und Verhalten von \(G_f\) an den Definitionslücken
Nullstelle von \(f\)
Einzige Nullstelle: \(x = -2\)
Ausführliche Erklärung (nicht verlangt)
\[f(x) = \frac{\textcolor{#0087c1}{-2x-4}}{\textcolor{#e9b509}{x^3+6x^2+9x}}\]
Die Nullstelle von \(f\) ist die Nullstelle des Zählerpolynoms, die nicht zugleich Nullstelle des Nennerpolynoms ist.
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
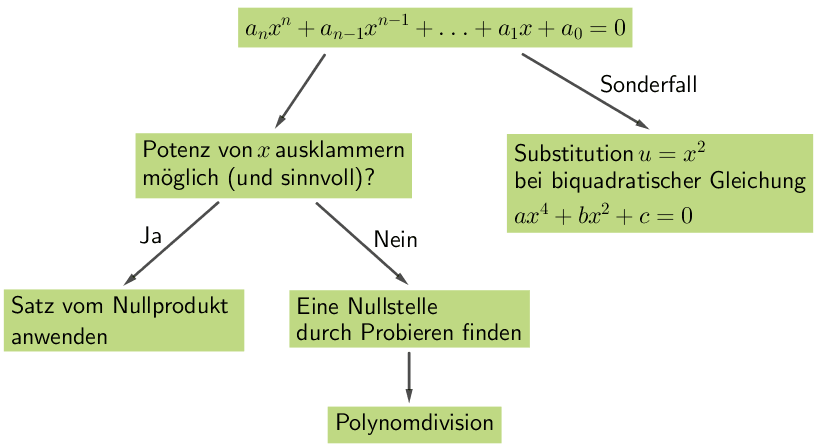
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
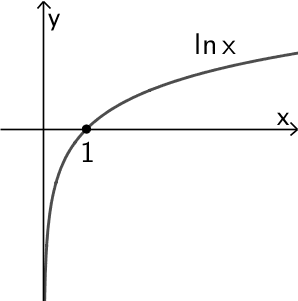
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
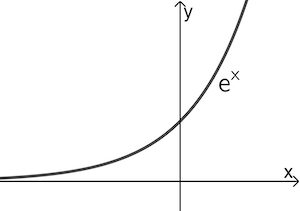
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
\[\begin{align*}f(x) = 0\;\Rightarrow \;\textcolor{#0087c1}{-2x - 4} &= 0 &&| + 4 \\[0.8em]-2x &= 4 &&| : (-2) \\[0.8em] x &= -2\end{align*}\]
Prüfen, ob \(x = -2\) zugleich Nullstelle des Nennerpolynoms ist
\[\begin{align*}(-2)^\textcolor{#e9b509}{3} \textcolor{#e9b509}{+} \textcolor{#e9b509}{6} \textcolor{#e9b509}{\cdot} (-2)^\textcolor{#e9b509}{2} \textcolor{#e9b509}{+} \textcolor{#e9b509}{9} \textcolor{#e9b509}{\cdot} (-2) &= -8 + 6 \cdot 4 -18 \\[0.8em] &= -2 \textcolor{#cc071e}{\neq} 0\end{align*}\]
Also ist \(x = -2\) einzige Nullstelle von \(f\).
Untersuchung von \(f\) auf Polstellen
Polstellen sind alle Nullstellen des Nennerpolynoms, die nicht zugleich Nullstellen des Zählerpolynoms sind. Ist eine Nennernullstelle vollständig kürzbar, hat die gebrochnrationale Funktion dort eine hebbare Definitionslücke. Dieser Fall wurde bereits ausgeschlossen (vgl. oben).
Nullstellen des Nennerpolynoms bestimmen:
\[\begin{align*}\textcolor{#e9b509}{x^3+6x^2+9x} &= 0 &&|\;x\;\text{ausklammern} \\[0.8em] x \cdot (\underbrace{x^2 + 6x + 9}_{a^2\,+\,2ab\,+\,b^2}) &= 0 &&|\;\text{1. Binom. Formel anwenden} \\[0.8em] x \cdot \underbrace{(x + 3)^2}_{(a\,+\,b)^2} &= 0\end{align*}\]
Daraus folgt:
\(x = 0\) ist einfache Nennernullstelle mit Vorzeichenwechsel (VZW) und damit Polstelle mit VZW.
\(x = -3\) ist doppelte Nennernullstelle ohne VZW und damit Polstelle ohne VZW.
Maximale Definitionsmenge \(D_f\)
Die Nennernullstellen (Polstellen) \(x = -3\) und \(x = 0\) sind auszuschließen.
Maximale Definitionsmenge bestimmen
Gebrochenrationale Funktion / Quotient von Funktionen
\[x \mapsto \dfrac{Zähler(x)}{\textcolor{#e9b509}{\underbrace{Nenner(x)}_{\Large{\neq \, 0}}}}\]
Nullstelle(n) des Nenners ausschließen!
Wurzelfunktion
\[x \mapsto \sqrt{\mathstrut\smash{\textcolor{#e9b509}{\underbrace{\dots}_{\Large{\geq\,0}}}}} \\ {}\]
Der Wert des Terms unter der Wurzel (Radikand ) darf nicht negativ sein!
(natürliche) Logarithmusfunktion
\(x \mapsto \ln{(\,\textcolor{#e9b509}{\underbrace{\dots}_{\Large{>\,0}}}\,)}\) bzw. \(x \mapsto \log_{a}{(\,\textcolor{#e9b509}{\underbrace{\dots}_{\Large{>\,0}}}\,)}\)
Die (Natürliche) Logarithmusfunktion ist in \(\textcolor{#e9b509}{\mathbb R^{+}}\) definiert!
\[\Rightarrow \;D_f = \mathbb R \backslash \{-3;0\}\]
Verhalten von \(G_f\) an den Definitionslücken
Zwei Möglichkeiten: Grenzwertbetrachtung am Funktionsterm oder mithilfe einer Vorzeichentabelle
1. Möglichkeit: Grenzwertbetrachtung am Funktionsterm
Die Art der Polstellen (mit/ohne VZW) ist bereits bekannt. Deshalb ist eine einseitige Grenzwertbetrachtung an den Definitionslücken (Polstellen) \(x = -3\) und \(x = 0\) ausreichend.
Linksseitige Grenzwertbetrachtung der Definitionslücke \(x = -3\):
\[\lim \limits_{\underset{x\,<\,-3}{x\,\to\,-3}} f(x) = \lim \limits_{\underset{x\,<\,-3}{x\,\to\,-3}}\, \frac{\textcolor{#0087c1}{\overbrace{-2x - 4}^{\to\,+2}}}{\textcolor{#e9b509}{\underbrace{x}_{\to\,-3}} \cdot \textcolor{#e9b509}{\underbrace{(x + 3)^2}_{\to\,0^+}}} = -\infty\]
Da \(x = -3\) eine Polstelle ohne VZW ist, folgt für die rechtsseitige Grenzwertbetrachtung:
\[\lim \limits_{\underset{x\,>\,-3}{x\,\to\,-3}} f(x) = -\infty\]
Linksseitige Grenzwertbetrachtung der Definitionslücke \(x = 0\):
\[\lim \limits_{\underset{x\,<\,0}{x\,\to\,0}} f(x) = \lim \limits_{\underset{x\,<\,0}{x\,\to\,0}}\, \frac{\textcolor{#0087c1}{\overbrace{-2x - 4}^{\to\,-4}}}{\textcolor{#e9b509}{\underbrace{x}_{\to\,0^-}} \cdot \textcolor{#e9b509}{\underbrace{(x + 3)^2}_{\to\,+9}}} = +\infty\]
Da \(x = 0\) eine Polstelle mit VZW ist, folgt für die rechtsseitige Grenzwertbetrachtung:
\[\lim \limits_{\underset{x\,>\,0}{x\,\to\,0}} f(x) = -\infty\]
2. Möglichkeit: Grenzwertbetrachtung mithilfe einer Vorzeichentabelle
\[f(x) = \frac{-2x-4}{x^3+6x^2+9x} = \frac{-2 \cdot (x + 2)}{\textcolor{#e9b509}{x} \cdot \textcolor{#e9b509}{(x + 3)^2}}\]
| \(x\) | linksseitig \(\underset{x\,<\,-3}{x \to -3}\) | rechtsseitig \(\underset{x\,>\,-3}{x \to -3}\) | linksseitig \(\underset{x\,<\,0}{x \to 0}\) | rechtsseitig \(\underset{x\,>\,0}{x \to 0}\) |
| \(-2\) | \(\textcolor{#cc071e}{–}\) | \(\textcolor{#cc071e}{–}\) | \(\textcolor{#cc071e}{–}\) | \(\textcolor{#cc071e}{–}\) |
| \((x + 2)\) | \(\textcolor{#cc071e}{–}\) | \(\textcolor{#cc071e}{–}\) | \(\textcolor{#0087c1}{+}\) | \(\textcolor{#0087c1}{+}\) |
| \(\textcolor{#e9b509}{x}\) | \(\textcolor{#cc071e}{–}\) | \(\textcolor{#cc071e}{–}\) | \(\textcolor{#cc071e}{0^-}\) | \(\textcolor{#0087c1}{0^+}\) |
| \(\textcolor{#e9b509}{(x + 3)^2}\) | \(\textcolor{#0087c1}{0^+}\) | \(\textcolor{#0087c1}{0^+}\) | \(\textcolor{#0087c1}{+}\) | \(\textcolor{#0087c1}{+}\) |
| \(f(x)\) | \(\textcolor{#cc071e}{–}\) | \(\textcolor{#cc071e}{–}\) | \(\textcolor{#0087c1}{+}\) | \(\textcolor{#cc071e}{–}\) |
| \(G_f\) | \(\textcolor{#cc071e}{\underset{-\infty}{\downarrow}}\) | \(\textcolor{#cc071e}{\underset{-\infty}{\downarrow}}\) | \(\textcolor{#0087c1}{\overset{+\infty}{\uparrow}}\) | \(\textcolor{#cc071e}{\underset{-\infty}{\downarrow}}\) |
Der Funktionsterm von \(f\) wird vollständig faktorisiert und von allen Faktoren das Vorzeichen für das links- und rechtsseitige Grenzwertverhalten an den Definitionslücken \(x = -3\) und \(x = 0\) bestimmt.
Von entscheidender Bedeutung sind die Nennerfaktoren \(\textcolor{#e9b509}{x}\) bzw. \(\textcolor{#e9b509}{(x + 3)^2}\), weil diese die Grenzwerte \(\textcolor{#cc071e}{0^-}\) bzw. \(\textcolor{#0087c1}{0^+}\) annehmen können und damit den asymptotischen Verlauf des Graphen von \(f\) nach \(\textcolor{#cc071e}{-\infty}\) bzw. \(\textcolor{#0087c1}{+\infty}\) an den senkrechten Asymptoten (gestrichelt) festlegen.
Erläuterung der ersten Spalte (gilt analog für alle anderen Spalten):
Für die linksseitige Grenzwertbetrachtung \(\underset{x\,<\,-3}{x \to -3}\) der Definitionslücke \(x = -3\) hat
- der Faktor \(-2\) im Zähler (ohnehin) das Vorzeichen \(\textcolor{#cc071e}{–}\),
- der Faktor \((x + 2)\) im Zähler das Vorzeichen \(\textcolor{#cc071e}{–}\),
- der Faktor \(\textcolor{#e9b509}{x}\) im Nenner das Vorzeichen \(\textcolor{#cc071e}{–}\) und
- nimmt der Faktor \(\textcolor{#e9b509}{(x + 3)^2}\) im Nenner den Grenzwert \(\textcolor{#0087c1}{0^+}\) (beliebig nahe \(0\) und positiv) an.
Somit folgt für den linksseitigen Verlauf von \(G_f\) an der Definitionslücke \(x = -3\):
\[\dfrac{\textcolor{#cc071e}{–}\, \cdot\, \textcolor{#cc071e}{–}}{\textcolor{#cc071e}{–}\, \cdot\, \textcolor{#0087c1}{0^+}} = \dfrac{\textcolor{#0087c1}{+}}{\textcolor{#cc071e}{0^-}} = \textcolor{#cc071e}{-\infty}\]
b) Untersuchen von \(G_f\) auf schräge oder waagrechte Asymptoten
Zwei Möglichkeiten: Grad des Zähler- /Nennerpolynoms vergleichen oder Grenzwertbetrachtung für \(x \to -\infty\) bzw. \(x \to +\infty\)
1. Möglichkeit: Grad des Zähler- /Nennerpolynoms vergleichen
\[f(x) = \frac{\textcolor{#0087c1}{-2x-4}}{\textcolor{#e9b509}{x^3+6x^2+9x}}; \;D_f = \mathbb R \backslash \{-3;0\}\]
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(z(x)\) und \(n(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(n(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
Da der Grad des Zählerpolynoms kleiner ist als der Grad des Nennerpolynoms, ist die \(x\)-Achse mit der Gleichung \(y = 0\) waagrechte Asymptote für das Verhalten von \(G_f\) für \(x \to -\infty\) bzw. \(x \to +\infty\).
2. Möglichkeit: Grenzwertbetrachtung für \(\boldsymbol{x \to -\infty}\) bzw. \(\boldsymbol{x \to +\infty}\)
Für eine aussagekräftige Grenzwertbetrachtung wird die höchste Potenz des Nennerpolynoms im Zähler und im Nenner ausgeklammert und gekürzt. Eine zusammenfassende Grenzwertbetrachtung für \(x \to \pm \infty\) ist ausreichend.
\[f(x) = \frac{-2x-4}{\textcolor{#e9b509}{x^3}+6x^2+9x}\]
\[\begin{align*}\lim \limits_{x\,\to\,\pm\infty} f(x) &= \lim \limits_{x\,\to\,\pm\infty} \frac{-2x-4}{x^3+6x^2+9x} &&| \; x^3\;\text{ausklammern und kürzen} \\[0.8em] &= \lim \limits_{x\,\to\,\pm\infty} \frac{\cancel{x^3} \cdot \Big( \frac{-2}{x^2} - \frac{4}{x^3} \Big)}{\cancel{x^3} \cdot \Big(1+\frac{6}{x} + \frac{9}{x^2} \Big)} \\[0.8em] &= \lim \limits_{x\,\to\,\pm\infty} \frac{\textcolor{#0087c1}{\overbrace{\frac{-2}{x^2} - \frac{4}{x^3}}^{\to\,0}}}{\textcolor{#e9b509}{\underbrace{1+\frac{6}{x} + \frac{9}{x^2}}_{\to\,1}} } \\[0.8em] &= 0\end{align*}\]
Somit ist die \(x\)-Achse mit der Gleichung \(y = 0\) waagrechte Asymptote von \(G_f\).
c) \(f(-4)\) und \(f(1)\) berechnen und \(G_f\) im Bereich \(-7 < x < 4\) in ein Koordinatensystem zeichnen
Funktionswerte \(f(-4)\) und \(f(1)\)
\[f(x) = \frac{-2x-4}{x^3+6x^2+9x}\]
\[\begin{align*}f(\textcolor{#e9b509}{-4}) &= \frac{-2 \cdot \textcolor{#e9b509}{(-4)}-4}{\textcolor{#e9b509}{(-4)}^3+6 \cdot \textcolor{#e9b509}{(-4)}^2+9 \cdot \textcolor{#e9b509}{(-4)}} \\[0.8em] &= \frac{4}{-64 + 96 - 36} = \frac{4}{-4} = -1\end{align*}\]
\[\begin{align*}f(\textcolor{#e9b509}{1}) &= \frac{-2 \cdot \textcolor{#e9b509}{1}-4}{\textcolor{#e9b509}{1}^3+6 \cdot \textcolor{#e9b509}{1}^2+9 \cdot \textcolor{#e9b509}{1}} = \frac{-6}{1 + 6 + 9} \\[0.8em] &= \frac{-6}{16} = - \frac{3}{8} = -0{,}375\end{align*}\]
Skizze von \(G_f\) im Bereich \(-7 \leq x \leq 4\)
Bisherige Ergebnisse:
- \(x = -2\) ist Nullstelle von \(f\) (vgl. Teilaufgaben a)
- \(x = -3\) ist Polstelle ohne VZW, \(x = 0\) ist Polstelle mit VZW
- \(G_f\) verläuft an der Polstelle \(x = -3\) beidseitig nach \(-\infty\), an der Polstelle \(x = 0\) linksseitig nach \(+\infty\) und rechtsseitig nach \(-\infty\)
- Für \(x \to \pm \infty\) ist die \(x\)-Achse \((y = 0)\) waagrechte Asymptote von \(G_f\) (vgl. Teilaufgabe b)
- \(G_f\) verläuft durch die Punkte \((-4|-1)\) und \((1|0{,}375)\) (vgl. Teilaufgabe c)
Mögliche Vorgehensweise
1. Senkrechte Asymptoten und waagrechte Asymptote einzeichnen
An den Polstellen \(x = -3\) und \(x = 0\) hat \(G_f\) jeweils eine senkrechte Asymptote.
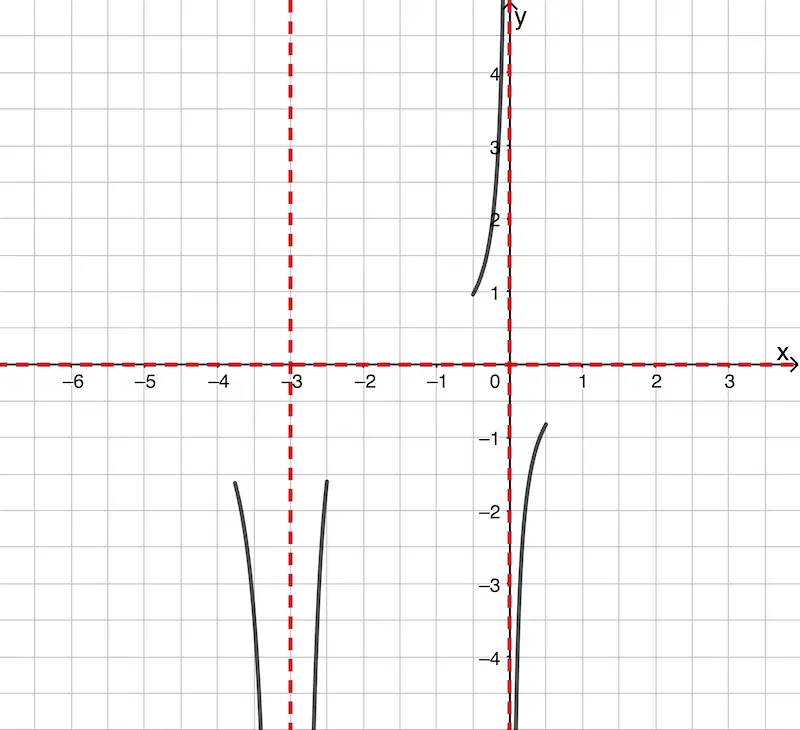
2. Verhalten von \(\boldsymbol{G_f}\) an den Definitionslücken (senkrechten Asymptoten) skizzieren
3. Punkte \(\boldsymbol{(-4|-1)}\) und \(\boldsymbol{(1|-0{,}375)}\) einzeichnen und Verlauf von \(\boldsymbol{G_f}\) im Unendlichen skizzieren
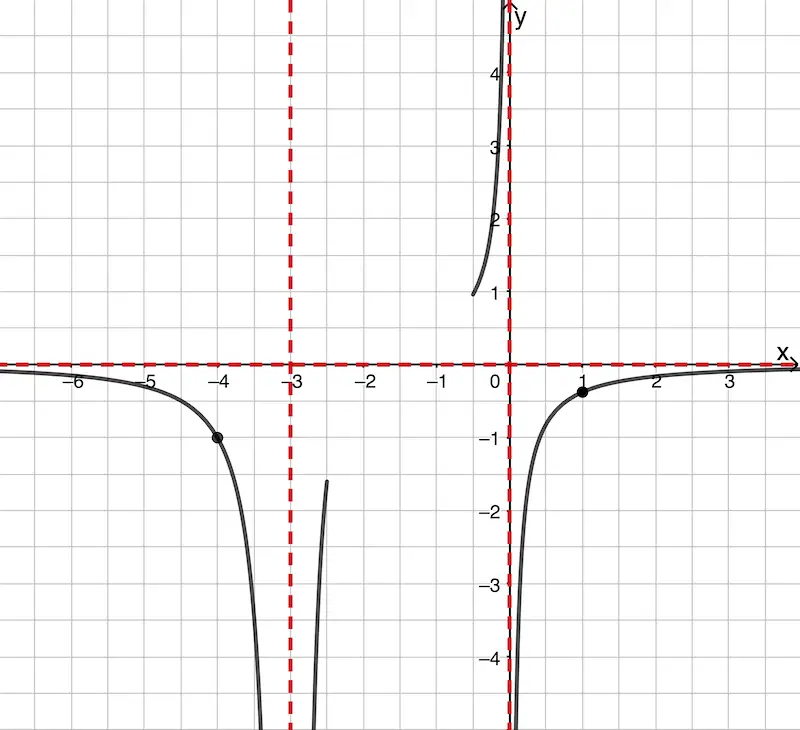
Die Punkte \((-4|-1)\) und \((1|0{,}375)\) liegen unterhalb der \(x\)-Achse. Da \(x = -2\) die einzige Nullstelle von \(f\) ist, muss sich \(G_f\) für \(x \to \pm \infty\) von unten der waagrechten Asymptote (\(x\)-Achse) annähern.
4. Punkt \(\boldsymbol{(-2|0)}\) einzeichnen und Skizze vervollständigen
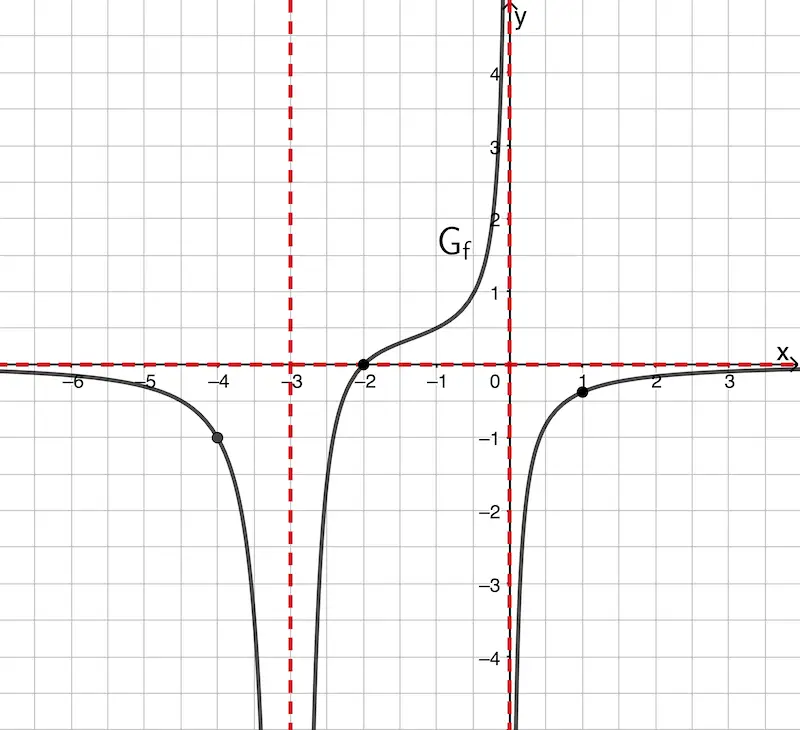
Da \(x = -2\) eine einfache Nullstelle mit VZW ist, schneidet \(G_f\) die \(x\)-Achse an dieser Stelle.
Ein möglichst genauer Verlauf von \(G_f\) im Bereich \(-2 < x < 0\) ist nicht verlangt. Hierfür wäre beispielsweise zusätzlich der Funktionswert \(f(-1)\) zu bestimmen.

