Gegeben ist die Funktion \(f \colon x \mapsto 4x^{2} - 1\).
a) Bestimmen Sie die mittlere Änderungsrate auf dem Intervall \([1;3]\).
b) Bestimmen Sie \(f'(2)\) unter Verwendung des Differentialquotienten.
a) Mittlere Änderungsrate von \(f\) auf dem Intervall \([1;3]\)
\[f(x) = 4x^{2} - 1\]
Die mittlere Änderungsrate (Differenzenquotient) der Funktion \(f\) auf dem Intervall \([1;3]\) entspricht der Steigung \(m_{S}\) der Sekante durch die Punkte \((1|f(1))\) und \((3|f(3))\) des Graphen der Funktion \(f\).
Differenzenquotient oder mittlere Änderungsrate
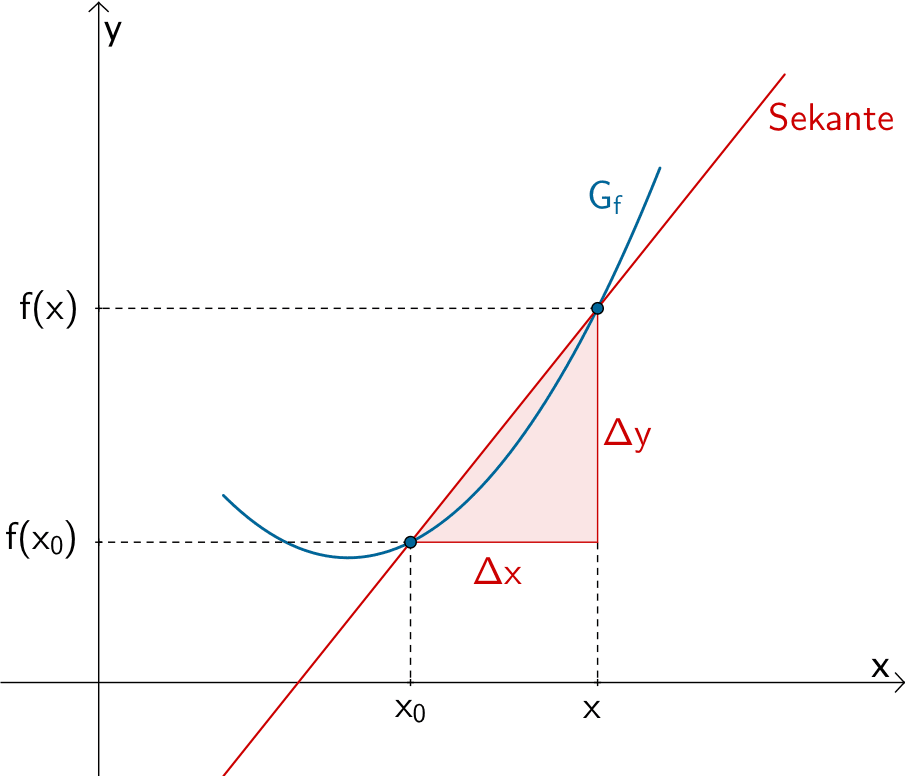
Der Differenzenquotient oder die mittlere Änderungsrate \(m_{s} = \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt die Steigung der Sekante durch den Punkt \((x_{0}|f(x_{0}))\) und einen weiteren Punkt des Graphen der Funktion \(f\).
\[\begin{align*} m_{S} &= \frac{f(3) - f(1)}{3 - 1} \\[0.8em] &= \frac{4 \cdot 3^{2} - 1 - (4 \cdot 1^{2} - 1)}{2} \\[0.8em] &= \frac{36 - 1 - 4 + 1}{2} \\[0.8em] &= \frac{32}{2} \\[0.8em] &= 16 \end{align*}\]
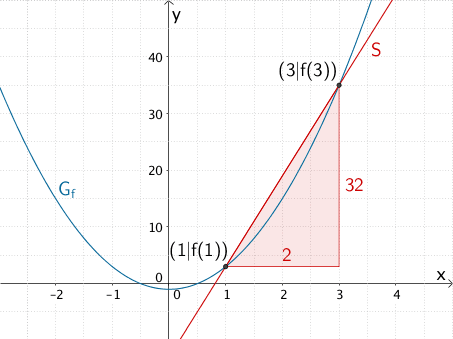
Steigung der Sekante \(S\) durch die Punkte \((1|f(1))\) und \((3|f(3))\) des Graphen \(G_{f}\) der Funktion \(f \colon x \mapsto 4x^{2} - 1\)
b) Bestimmung von \(f'(2)\) unter Verwendung des Differentialquotienten
Der Grenzwert \(\lim \limits_{x\,\to\,x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) (Differentialquotient) heißt die Ableitung der Funktion \(\boldsymbol{f}\) an der Stelle \(\boldsymbol{x_{0}}\) und wird mit \(f'(x_{0})\) bezeichnet.
Differentialquotient oder lokale bzw. momentane Änderungsrate
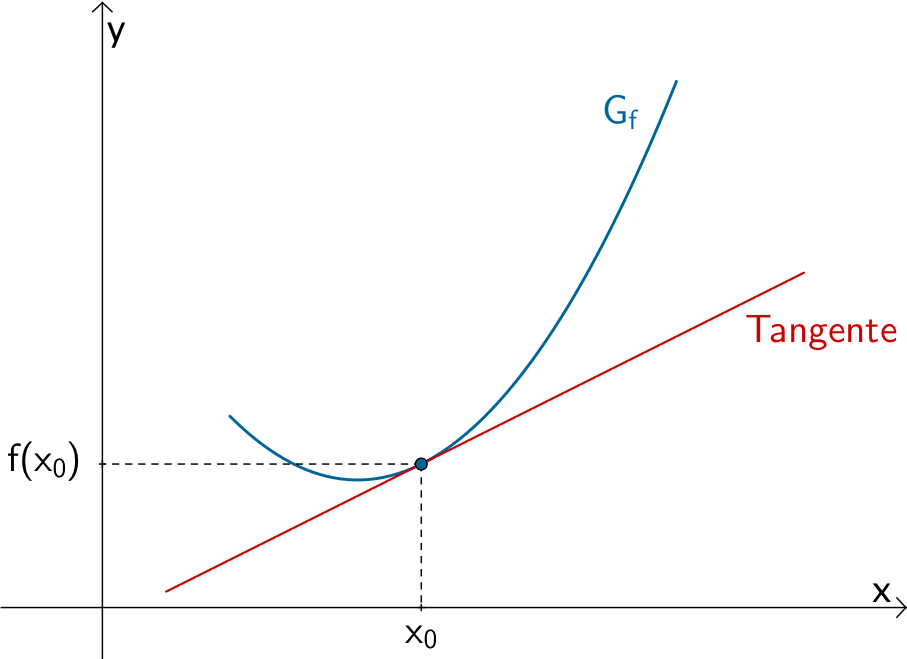
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
\[f'(x_{0}) = \lim \limits_{x\,\to\,x_{0}} \frac{f(x) - f(x_{0})}{x - x_{0}}\]
Bei der Bestimmung von \(f'(x_{0})\) unter Verwendung des Differentialquotienten (anstatt der Anwendung von Ableitungsregeln) kommt es auf eine geeignete Umformung des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) an, sodass eine aussagekräftige Beurteilung des Grenzwerts \(\lim \limits_{x\,\to\,x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) möglich ist.
Im vorliegenden Fall führt der Grenzwert \(\lim \limits_{x\,\to\,2} \dfrac{4x^{2} - 16}{x - 2}\) (vgl. unten) auf den unbestimmten Ausdruck \(\dfrac{0}{0}\). Erst nach der Anwendung der 3. Binomischen Formel lässt sich der Grenzwert bestimmen.
\[f(x) = 4x^{2} - 1\]
\[x_{0} = 2\]
\[\begin{align*} f'(2) &= \lim \limits_{x\,\to\,2} \frac{f(x) - f(2)}{x - 2} \\[0.8em] &= \lim \limits_{x\,\to\,2} \frac{4x^{2} - 1 - (4 \cdot 2^{2} - 1)}{x - 2} \\[0.8em] &= \lim \limits_{x\,\to\,2} \frac{4x^{2} - 1 - 16 + 1}{x - 2} \\[0.8em] &= \lim \limits_{x\,\to\,2} \frac{4x^{2} - 16}{x - 2} & &| \; \text{Faktor}\;4\;\text{ausklammern} \\[0.8em] &= \lim \limits_{x\,\to\,2} \frac{4 \cdot (\overbrace{x^{2} - 4}^{\large{a^{2}\,-\,b^{2}}})}{x - 2} & &| \;\text{3. Binom. Formel anwenden} \\[0.8em] &= \lim \limits_{x\,\to\,2} \frac{4 \cdot \overbrace{(x - 2)(x + 2)}^{\large{(a\,-\,b)(a\,+\,b)}}}{x - 2} & &| \;\text{Faktor}\;(x - 2)\;\text{kürzen} \\[0.8em] &= \lim \limits_{x\,\to\,2} \frac{4 \cdot \cancel{(x - 2)} (x + 2)}{\cancel{x - 2}} & &| \; (x \neq 2) \\[0.8em] &= \lim \limits_{x\,\to\,2} 4 \cdot (x + 2) \\[0.8em] &= 16 \end{align*}\]
Alternative: \(h\)-Methode anwenden:
Eine gleichwertige Formulierung des Differentialquotienten liefert die sogenannte \(h\)-Methode.
\[f'(x_{0}) = \lim \limits_{h\,\to\,0} \frac{f(x_{0} + h) - f(x_{0})}{h}\]
Auch damit führt der Grenzwert \(\lim \limits_{h\,\to\,0} \dfrac{4h^{2} + 16h}{h}\) (vgl. unten) auf den unbestimmten Ausdruck \(\dfrac{0}{0}\). Durch Ausklammern und Kürzen des Faktors \(h\) lässt sich der Grenzwert bestimmen.
\[f(x) = 4x^{2} - 1\]
\[x_{0} = 2\]
\[\begin{align*} f'(2) &= \lim \limits_{h\,\to\,0} \frac{f(2 + h) - f(2)}{h} \\[0.8em] &= \lim \limits_{h\,\to\,0} \frac{4 \cdot \overbrace{(2 + h)^{2}}^{\large{(a\,+\,b)^{2}}} - 1 - (4 \cdot 2^{2} - 1)}{h} & &| \; \text{1. Binom. Formel anwenden} \\[0.8em] &= \lim \limits_{h\,\to\,0} \frac{4 \cdot (\overbrace{4 + 4h + h^{2}}^{\large{a^{2}\,+\,2ab\,+\,b^{2}}}) - 1 - 16 + 1}{h} \\[0.8em] &= \lim \limits_{h\,\to\,0} \frac{4h^{2} + 16h}{h} & &| \; \text{Faktor}\; h \; \text{ausklammern} \\[0.8em] &= \lim \limits_{h\,\to\,0} \frac{h \cdot (4h + 16)}{h} & &| \; \text{Faktor}\;h\;\text{kürzen} \\[0.8em] &= \lim \limits_{h\,\to\,0} \frac{\cancel{h} \cdot (4h + 16)}{\cancel{h}} & &| \; (h \neq 0) \\[0.8em] &= \lim \limits_{h\,\to\,0} (4h + 16) \\[0.8em] &= 16 \end{align*}\]

