Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{x(x-3)}{(x-2)^2}\) mit maximaler Definitionsmenge \(D_f\).
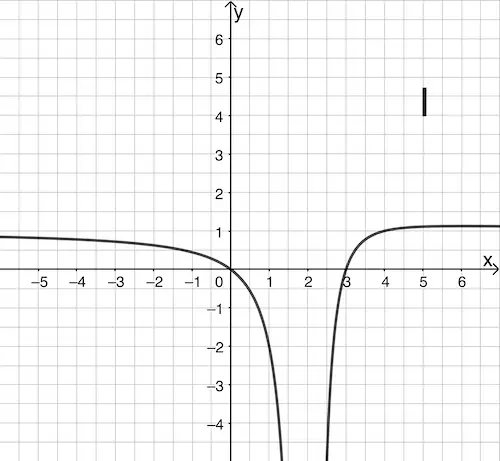
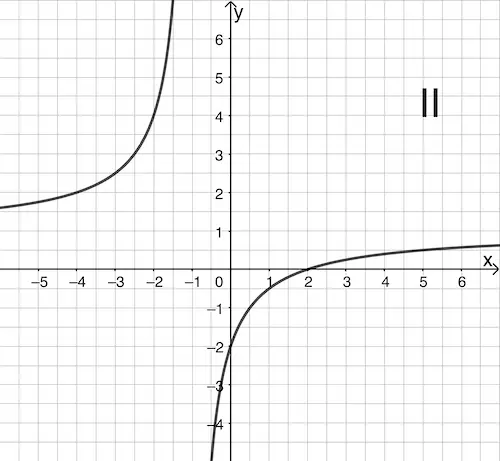
a) Geben Sie \(D_f\) an und entscheiden Sie, welcher der Graphen I bis IV den Graphen der Funktion \(f\) darstellt. Begründen Sie Ihre Entscheidung.
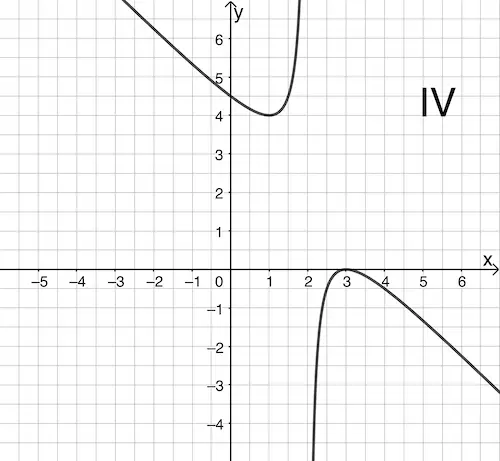
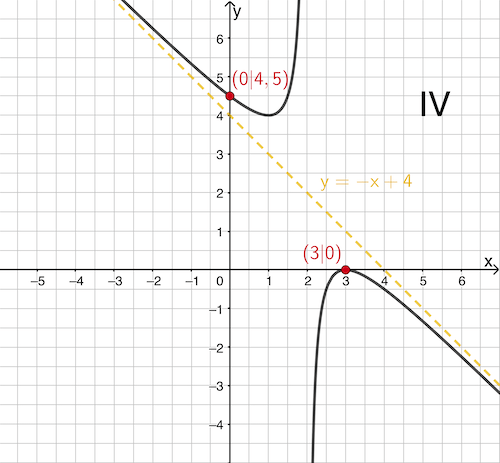
b) Graph IV zeigt den Graphen einer gebrochenrationalen Funktion \(g\), der eine schräge Asymptote mit der Gleichung \(y = -x + 4\) besitzt. Die Koordinaten der Schnittpunkte des Graphen von \(g\) mit den Koordinatenachsen sowie die Polstelle von \(g\) sind ganzzahlig.
Geben Sie an, welcher der folgenden Funktionsterme die Funktion \(g\) beschreibt.
\[\text{A}\quad\frac{1}{x - 2} -x +4\]
\[\text{B}\quad-\frac{1}{x-2} -x +4\]
\[\text{C}\quad\frac{1}{2-x} +x - 4\]
\[\text{D}\quad\frac{1}{2-x}-x-4\]
a) Maximale Definitionsmenge, Funktionsgraph zuordnen und begründen
Maximale Definitionsmenge von \(f\)
\[f(x) = \frac{x(x-3)}{\textcolor{#e9b509}{(x-2)^2}}\]
Die Nennernullstelle \(\textcolor{#e9b509}{x = 2}\) ist aus dem Definitionsbereich auszuschließen.
Maximale Definitionsmenge bestimmen
Gebrochenrationale Funktion / Quotient von Funktionen
\[x \mapsto \dfrac{Zähler(x)}{\textcolor{#e9b509}{\underbrace{Nenner(x)}_{\Large{\neq \, 0}}}}\]
Nullstelle(n) des Nenners ausschließen!
Wurzelfunktion
\[x \mapsto \sqrt{\mathstrut\smash{\textcolor{#e9b509}{\underbrace{\dots}_{\Large{\geq\,0}}}}} \\ {}\]
Der Wert des Terms unter der Wurzel (Radikand ) darf nicht negativ sein!
(natürliche) Logarithmusfunktion
\(x \mapsto \ln{(\,\textcolor{#e9b509}{\underbrace{\dots}_{\Large{>\,0}}}\,)}\) bzw. \(x \mapsto \log_{a}{(\,\textcolor{#e9b509}{\underbrace{\dots}_{\Large{>\,0}}}\,)}\)
Die (Natürliche) Logarithmusfunktion ist in \(\textcolor{#e9b509}{\mathbb R^{+}}\) definiert!
\[\Rightarrow \; D_f = \mathbb R \backslash \{\textcolor{#e9b509}{2}\}\]
Funktionsgraph zuordnen und begründen
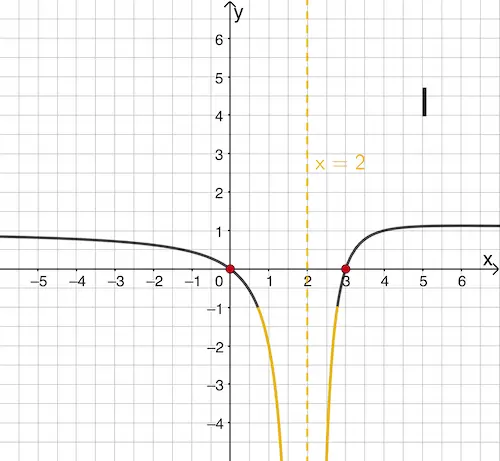
Graph I zeigt den Graphen der Funktion \(f\).
Begründung
\[f(x) = \frac{\textcolor{#cc071e}{x(x-3)}}{\textcolor{#e9b509}{(x-2)^2}}\]
Da die Nennernullstelle \(\textcolor{#e9b509}{x = 2}\) von \(f\) eine doppelte Nullstelle ist, ist \(x = 2\) eine Polstelle ohne Vorzeichenwechsel und der Graph von \(f\) verläuft beidseitig der senkrechten Asymptote mit der Gleichung \(x = 2\) gleichermaßen nach Unendlich. Dieses Verhalten zeigt nur Graph I.
oder
Dem Zähler des Funktionsterm von \(f\) lassen sich die einfachen Nullstellen \(\textcolor{#cc071e}{x = 0}\) und \(\textcolor{#cc071e}{x = 3}\) entnehmen. Graph I schneidet als einziger die \(x\)-Achse an diesen Stellen.
 (Eintragungen nicht verlangt)
(Eintragungen nicht verlangt)
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(z(x)\) und \(n(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(n(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
Anmerkung
Da der Grad des Zählerpolynoms gleich dem Grad des Nennerpolynoms ist (Grad 2), besitzt der Graph der Funktion \(f\) für \(x \to -\infty\) bzw. \(x \to +\infty\) eine waagrechte Asymptote, die parallel zur \(\textcolor{#0087c1}{x}\)-Achse verläuft. Die Gleichung der waagrechten Asymptote ergibt sich aus dem Quotienten der Koeffizienten der höchsten Potenzen des Zähler- bzw. Nennerpolynoms.
\[f(x) = \frac{x(x-3)}{(x-2)^2} = \frac{\textcolor{#0087c1}{1 \cdot x^2} - 3x}{\textcolor{#0087c1}{1 \cdot x^2} - 4x +4}\]
Gleichung der waagrechten Asymptote: \(y = \dfrac{\textcolor{#0087c1}{1}}{\textcolor{#0087c1}{1}} = 1\)
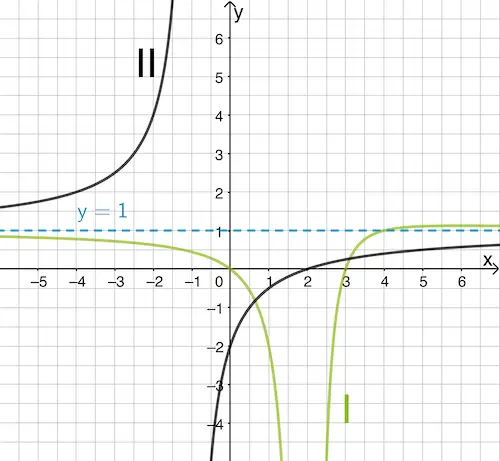
Nun zeigt aber sowohl Graph I als auch Graph II eine waagrechte Asymptote mit der Gleichung \(y = 1\). Deshalb eignet sich diese Eigenschaft des Graphen von \(f\) nicht für eine eindeutige Zuordnung.
b) Funktionsterm dem Graphen von \(g\) (Graph IV) zuordnen
Der Funktionsterm B beschreibt die Funktion \(g\).
Begründung (nicht verlangt)
Die Funktionsterme A bis D sind in der polynomdividirten Form gegeben. Die Summe aus gebrochenrationalem und linearem Term ermöglicht eine unkomplizierte Grenzwertbetrachtung für \(x \to -\infty\) bzw. \(x \to +\infty\). Der lineare Term entspricht hier immer dem Term der schrägen Asymptote, weil der gebrochenrationale Term immer den Grenzwert null annimmt.
Da der Graph der Funktion \(g\) (Graph IV) eine schräge Asymptote mit der Gleichung \(\textcolor{#e9b509}{y = -x + 4}\) besitzt, muss gelten:
\[\lim \limits_{x\,\to\,\pm\infty}g(x) = \lim \limits_{x\,\to\,-\infty} (\textcolor{#e9b509}{-x + 4})\]
Dieses Grenzwertverhalten erfüllen nur die Terme A und B.
\[\text{A} \quad \lim \limits_{x\,\to\,\pm\infty}\bigg(\textcolor{#e9b509}{\underbrace{\frac{1}{x - 2}}_{\to\,0}} -x +4\bigg) = \lim \limits_{x\,\to\,\pm\infty} (\textcolor{#e9b509}{-x + 4})\enspace \textcolor{#89ba17}{\Large{\checkmark}}\]
\[\text{B} \quad \lim \limits_{x\,\to\,\pm\infty}\bigg(-\textcolor{#e9b509}{\underbrace{\frac{1}{x - 2}}_{\to\,0}} -x +4\bigg) = \lim \limits_{x\,\to\,\pm\infty} (\textcolor{#e9b509}{-x + 4})\enspace \textcolor{#89ba17}{\Large{\checkmark}}\]
Bei den Termen C und D liefert die Grenzwertbetrachtung eine andere schräge Asymptote.
\[\begin{align*}\text{C} \quad \lim \limits_{x\,\to\,\pm\infty}\bigg(\textcolor{#e9b509}{\underbrace{\frac{1}{2-x}}_{\to\,0}} +x -4\bigg) &= \lim \limits_{x\,\to\,\pm\infty} (x - 4)\\[0.8em] &\neq \lim \limits_{x\,\to\,\pm\infty} (\textcolor{#e9b509}{-x + 4}) \end{align*}\]
\[\begin{align*}\text{D} \quad \lim \limits_{x\,\to\,\pm\infty}\bigg(\textcolor{#e9b509}{\underbrace{\frac{1}{2-x}}_{\to\,0}} -x -4\bigg) &= \lim \limits_{x\,\to\,\pm\infty} (-x - 4)\\[0.8em] &\neq \lim \limits_{x\,\to\,\pm\infty} (\textcolor{#e9b509}{-x + 4}) \end{align*}\]
Eine Punktprobe mit einem der Schnittpunkte mit den Koordinatenachsen \(\textcolor{#cc071e}{(3|0)}\) oder \(\textcolor{#cc071e}{(0|4{,}5)}\) zeigt, ob
der Funktionsterm \(\text{A}\quad\dfrac{1}{x - 2} -x +4\) oder
der Funktionsterm \(\text{B}\quad-\dfrac{1}{x-2} -x +4\)
die Funktion \(g\) beschreibt.
\[\begin{align*}\text{A}\quad \textcolor{#cc071e}{0} &= \frac{1}{\textcolor{#cc071e}{3} - 2} - \textcolor{#cc071e}{3} +4 \\[0.8em] 0 &\neq 2 \end{align*}\]
\[\begin{align*}\text{B}\quad \textcolor{#cc071e}{0} &= -\frac{1}{\textcolor{#cc071e}{3}-2} -\textcolor{#cc071e}{3} +4 \\[0.8em] 0 &= 0\enspace \textcolor{#89ba17}{\Large{\checkmark}} \end{align*}\]
Also beschreibt der Funktionsterm B die Funktion \(g\).


