Beschreiben Sie unter Verwendung einer geeigneten Skizze, wie sich nachweisen lässt, dass eine Gerade orthogonal zu einer Ebene ist.
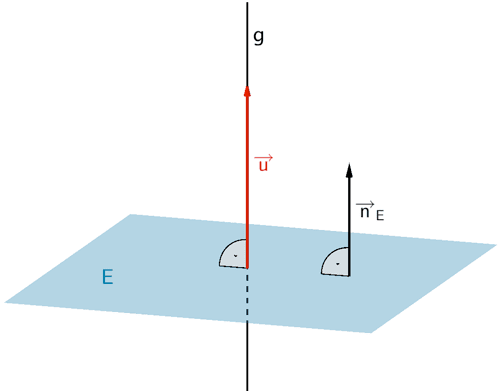
Eine Gerade \(g\) verläuft orthogonal (senkrecht) zu einer Ebene \(E\) \((g \perp E)\), wenn der Richtungsvektor \(\overrightarrow{u}\) der Gleichung der Geraden \(g\) und der Normalenvektor \(\overrightarrow{n}_{E}\) der Gleichung der Ebene \(E\) in Normalenform zueinander parallel sind. Die Vektoren \(\overrightarrow{u}\) und \(\overrightarrow{n}_{E}\) müssen somit linear abhängig sein und es muss gelten (vgl. Abiturskript - 2.3.4 Lotgeraden und orthogonale Ebenen, Seite 3 - Lotgerade zu einer Ebene ):
Lineare (Un-)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} = k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} \neq k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
Bei der Untersuchung der linearen (Un)Abhängigkeit dreier Vektoren spielt es keine Rolle, welche der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) oder \(\overrightarrow{c}\) man als Linearkombination der beiden anderen Vektoren darzustellen versucht.
\[\overrightarrow{u} = k \cdot \overrightarrow{n}_{E}; \; k \in \mathbb R\]
bzw.
\[\overrightarrow{n}_{E} = k \cdot \overrightarrow{u}; \; k \in \mathbb R\]
Anmerkung:
Liegt die Gleichung einer Ebene \(E\) in der Parameterform \(E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} + \mu \cdot \overrightarrow{v}; \; \lambda, \mu \in \mathbb R\) vor (vgl. Abiturskript - 2.2.2 Ebenengleichung in Parameterform) und soll die Orthogonalität einer Geraden \(g \colon \overrightarrow{X} = \overrightarrow{P} + \sigma \cdot \overrightarrow{w}; \; \sigma \in \mathbb R\) zu dieser Ebene nachgewiesen werden, so müssen folgende Bedingungen erfüllt sein:
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\left. \begin{align*} &\overrightarrow{w} \circ \overrightarrow{u} = 0 \quad \Longleftrightarrow \quad \overrightarrow{w} \perp \overrightarrow{u} \\[0.8em] &\text{und} \\[0.8em] &\overrightarrow{w} \circ \overrightarrow{v} = 0 \quad \Longleftrightarrow \quad \overrightarrow{w} \perp \overrightarrow{v} \end{align*} \right\} \enspace \Rightarrow \enspace g \perp E\]
Es ist in diesem Fall also nachzuweisen, dass der Richtungsvektor \(\overrightarrow{w}\) der Gleichung der Geraden \(g\) zu beiden Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{v}\) der Ebenengleichung in Parameterform senkrecht ist.

