Mathematik Klausur Q11/1-004 Bayern
Aufgabe 1
Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{8x}{x^{2} + 4}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Überprüfen Sie das Symmetrieverhalten von \(G_{f}\) bezüglich des Koordinatensystems.
b) Bestimmen Sie den maximalen Definitionsbereich der Funktion \(f\) und ermitteln Sie das Verhalten von \(f\) an den Rändern des Definitionsbereichs. Geben Sie die Gleichungen aller Asymptoten von \(G_{f}\) an.
c) Weisen Sie nach, dass der Graph \(G_{f}\) durch den Koordinatenursprung \(O(0|0)\) verläuft und berechnen Sie die Größe des Winkels, unter dem \(G_{f}\) die \(x\)-Achse schneidet.
(Teilergebnis: \(f'(x) = -\dfrac{8(x^{2} - 4)}{(x^{2} + 4)^{2}}\))
d) Bestimmen Sie die Lage und die Art der Extrempunkte von \(G_{f}\).
e) Zeichnen Sie den Graphen \(G_{f}\) unter Berücksichtigung der bisherigen Ergebnisse in ein geeignetes Koordinatensystem.
Aufgabe 2
Der Graph \(G_{f}\) einer gebrochenrationalen Funktion \(f\) hat folgende Eigenschaften:
\(G_{f}\) hat genau die zwei Nullstellen \(x = 0\) und \(x = 4\).
\(G_{f}\) hat genau die zwei Polstellen mit Vorzeichenwechsel \(x = -1\) und \(x = 2\).
\(G_{f}\) hat eine waagrechte Asymptote mit der Gleichung \(y = 2\).
a) Geben Sie einen möglichen Funktionsterm der Funktion \(f\) an und skizzieren Sie den Graphen der Funktion \(f\).
b) „Der Funktionsterm \(f(x)\) ist durch die genannten Eigenschaften eindeutig bestimmt." Nehmen Sie zu dieser Aussage begründend Stellung.
Aufgabe 3
Gegeben ist die in \(\mathbb R\) definierte Funktionenschar \(f_{a}(x) = x^{3} - ax + 3\) mit \(a \in \mathbb R\). Die Kurvenschar der Funktionenschar \(f_{a}\) wird mit \(G_{f_{a}}\) bezeichnet.
Bestimmen Sie den Wert des Parameters \(a\) so, dass der zugehörige Graph der Kurvenschar \(G_{f_{a}}\)
a) zwei Extrempunkte
b) einen Terrassenpunkt
besitzt.
Aufgabe 4
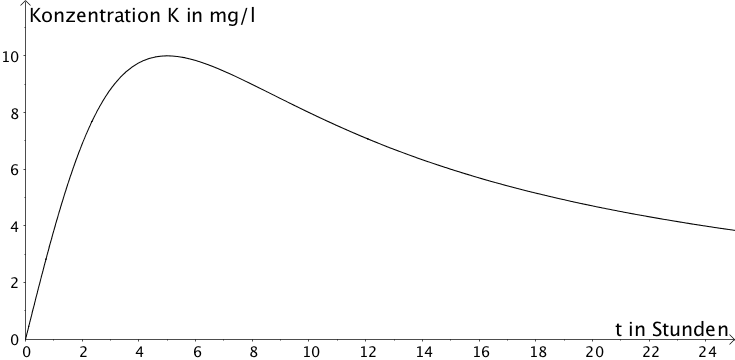
Nach der Einnahme eines Medikaments wird die Konzentration \(K\) des Medikaments im Blut eines Patienten gemessen.
Die Funktion \(K \colon t \mapsto \dfrac{100t}{t^{2} + 25}\) mit \(t \geq 0\) beschreibt näherungsweise den Verlauf \(K(t)\) der Konzentration des Medikaments in Milligramm pro Liter in Abhängigkeit von der Zeit \(t\) in Stunden (vgl. Abbildung).
a) Bestimmen Sie den Zeitpunkt nach der Einnahme des Medikaments, zu dem die Konzentration \(K\) des Medikaments im Blut des Patienten noch 10 % der maximalen Konzentration beträgt auf Minuten genau.
(Teilergebnis: \(K'(t) = -\dfrac{100(t^{2} - 25)}{(t^{2} + 25)^{2}}\))
b) Berechnen Sie die mittlere Änderungsrate der Konzentration \(K\) im Zeitintervall \([10;20]\) und interpretieren Sie das Ergebnis im Sachzusammenhang.
Aufgabe 5
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto f(x)\) mit
\[f(x) = \vert 2x - 4 \vert = \begin{cases} \begin{align*} 2x - 4 \; \text{falls} \; &x \geq 0 \\[0.8em] -(2x - 4) \; \text{falls} \; &x < 0 \end{align*} \end{cases}\]
Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Skizzieren Sie \(G_{f}\) in ein geeignetes Koordinatensystem und begründen Sie geometrisch, dass die Funktion \(f\) an der Stelle \(x = 2\) nicht differenzierbar ist.
b) Bestätigen Sie durch Rechnung, dass die Funktion \(f\) an der Stelle \(x = 2\) nicht differenzierbar ist.
- Details
- Hauptkategorie: Klausuren Q11/1
Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{8x}{x^{2} + 4}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Überprüfen Sie das Symmetrieverhalten von \(G_{f}\) bezüglich des Koordinatensystems.
b) Bestimmen Sie den maximalen Definitionsbereich der Funktion \(f\) und ermitteln Sie das Verhalten von \(f\) an den Rändern des Definitionsbereichs. Geben Sie die Gleichungen aller Asymptoten von \(G_{f}\) an.
c) Weisen Sie nach, dass der Graph \(G_{f}\) durch den Koordinatenursprung \(O(0|0)\) verläuft und berechnen Sie die Größe des Winkels, unter dem \(G_{f}\) die \(x\)-Achse schneidet.
(Teilergebnis: \(f'(x) = -\dfrac{8(x^{2} - 4)}{(x^{2} + 4)^{2}}\))
d) Bestimmen Sie die Lage und die Art der Extrempunkte von \(G_{f}\).
e) Zeichnen Sie den Graphen \(G_{f}\) unter Berücksichtigung der bisherigen Ergebnisse in ein geeignetes Koordinatensystem.
- Details
- Hauptkategorie: Klausuren Q11/1
Der Graph \(G_{f}\) einer gebrochenrationalen Funktion \(f\) hat folgende Eigenschaften:
\(G_{f}\) hat genau die zwei Nullstellen \(x = 0\) und \(x = 4\).
\(G_{f}\) hat genau die zwei Polstellen mit Vorzeichenwechsel \(x = -1\) und \(x = 2\).
\(G_{f}\) hat eine waagrechte Asymptote mit der Gleichung \(y = 2\).
a) Geben Sie einen möglichen Funktionsterm der Funktion \(f\) an und skizzieren Sie den Graphen der Funktion \(f\).
b) „Der Funktionsterm \(f(x)\) ist durch die genannten Eigenschaften eindeutig bestimmt." Nehmen Sie zu dieser Aussage begründend Stellung.
- Details
- Hauptkategorie: Klausuren Q11/1
Gegeben ist die in \(\mathbb R\) definierte Funktionenschar \(f_{a}(x) = x^{3} - ax + 3\) mit \(a \in \mathbb R\). Die Kurvenschar der Funktionenschar \(f_{a}\) wird mit \(G_{f_{a}}\) bezeichnet.
Bestimmen Sie den Wert des Parameters \(a\) so, dass der zugehörige Graph der Kurvenschar \(G_{f_{a}}\)
a) zwei Extrempunkte
b) einen Terrassenpunkt
besitzt.
- Details
- Hauptkategorie: Klausuren Q11/1
Nach der Einnahme eines Medikaments wird die Konzentration \(K\) des Medikaments im Blut eines Patienten gemessen.
Die Funktion \(K \colon t \mapsto \dfrac{100t}{t^{2} + 25}\) mit \(t \geq 0\) beschreibt näherungsweise den Verlauf \(K(t)\) der Konzentration des Medikaments in Milligramm pro Liter in Abhängigkeit von der Zeit \(t\) in Stunden (vgl. Abbildung).
a) Bestimmen Sie den Zeitpunkt nach der Einnahme des Medikaments, zu dem die Konzentration \(K\) des Medikaments im Blut des Patienten noch 10 % der maximalen Konzentration beträgt auf Minuten genau.
(Teilergebnis: \(K'(t) = -\dfrac{100(t^{2} - 25)}{(t^{2} + 25)^{2}}\))
b) Berechnen Sie die mittlere Änderungsrate der Konzentration \(K\) im Zeitintervall \([10;20]\) und interpretieren Sie das Ergebnis im Sachzusammenhang.
- Details
- Hauptkategorie: Klausuren Q11/1
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto f(x)\) mit
\[f(x) = \vert 2x - 4 \vert = \begin{cases} \begin{align*} 2x - 4 \; \text{falls} \; &x \geq 2 \\[0.8em] -(2x - 4) \; \text{falls} \; &x < 2 \end{align*} \end{cases}\]
Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Skizzieren Sie \(G_{f}\) in ein geeignetes Koordinatensystem und begründen Sie geometrisch, dass die Funktion \(f\) an der Stelle \(x = 2\) nicht differenzierbar ist.
b) Bestätigen Sie durch Rechnung, dass die Funktion \(f\) an der Stelle \(x = 2\) nicht differenzierbar ist.
- Details
- Hauptkategorie: Klausuren Q11/1
2023 Christian Rieger・mathelike
