Geben Sie von folgenden Funktionen jeweils die maximale Definitionsmenge an und bestimmen Sie jeweils die Nullstelle(n). Bilden Sie jeweils die Ableitungsfunktion und vereinfachen Sie soweit wie möglich.
a) \(f(x) = 2\ln{(3\sqrt{x})}\)
b) \(g(x) = xe^{4 - 3x} + \dfrac{x^{2}}{e^{3x - 4}}\)
c) \(h(x) = x^{3} \cdot \sin{\left( \dfrac{\pi}{3}x \right)}\)
Anmerkung:
Die maximale Definitionsmenge der Funktionen \(f\), \(g\) und \(h\) ist jeweils lediglich anzugeben. Jede diesbezügliche Erklärung oder Rechnung kann entfallen.
a) Funktion \(f(x) = 2\ln{(3\sqrt{x})}\)
Maximale Definitionsmenge der Funktion \(f\)
Die Natürliche Logarithmusfunktion ist in \(\mathbb R^{+}\) definiert.
\[\begin{align*} \Longrightarrow \quad 3\sqrt{x} &> 0 & &| : 3 \\[0.8em] \sqrt{x} &> 0 \\[0.8em] x &> 0 \end{align*}\]
\[\Longrightarrow \quad D_{f} = \mathbb R^{+}\]
Nullstelle(n) der Funktion \(f\)
\[f(x) = 2\ln{(3\sqrt{x})}\]
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(x = 1\), d. h. es gilt \(\ln{1} = 0\) (vgl. Abiturskript - 1.3.1 Eigenschaften und Rechenregeln, Natürliche Exponential- und Logarithmusfunktion).
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
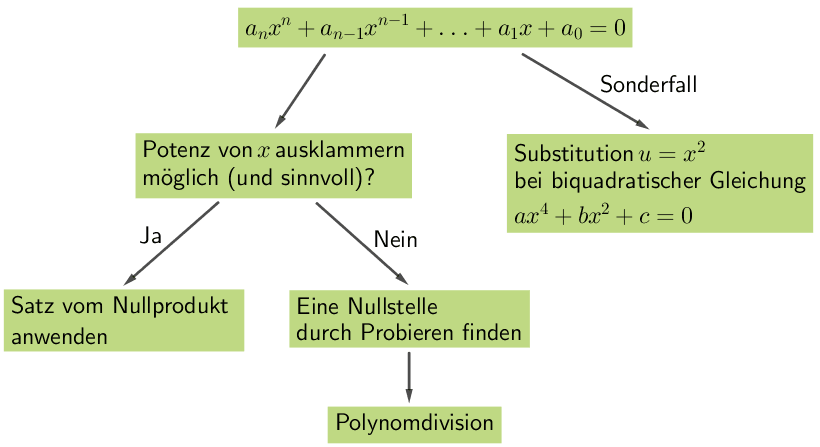
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
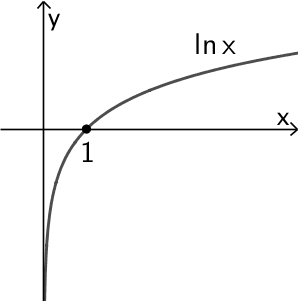
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
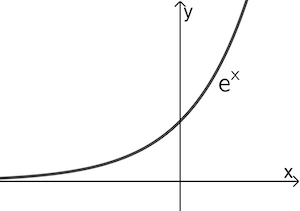
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
Unter Anwendung der Rechenregeln für Logarithmen bzw. Potenzen ergeben sich weitere Möglichkeiten, die Nullstelle(n) von \(f\) zu bestimmen.
\[\begin{align*} f(x) &= 0 \\[0.8em] 2\ln{\left(3\sqrt{x}\right)} &= 0 & &| : 2 \\[0.8em] \ln{\left(3\sqrt{x}\right)} &= 0 &&| \; \ln{1} = 0 \\[0.8em] 3\sqrt{x} &= 1 &&| : 3 \\[0.8em] \sqrt{x} &= \frac{1}{3} &&| (\dots)^{2}\; \text{(Quadrieren)} \\[0.8em] x &= \frac{1}{9}\end{align*}\]
oder
\[\begin{align*} f(x) &= 0 \\[0.8em] 2\ln{\left(3\sqrt{x}\right)} &= 0 & &| : 2 \\[0.8em] \ln{\left(3\sqrt{x}\right)} &= 0 &&| \; e^{(\dots)} \; \text{(zur Basis}\; e \; \text{potenzieren)} \\[0.8em] e^{\ln{\left(3\sqrt{x}\right)}} &= e^{0} &&| \; e^{\ln{x}} = x; \; \left( \text{allg.:} \; a^{\log_{a}{x}} = x \right), a^{0} = 1; \; \text{hier:} \; e^{0} = 1 \\[0.8em] 3\sqrt{x} &= 1 &&| : 3 \\[0.8em] \sqrt{x} &= \frac{1}{3} &&| (\dots)^{2}\; \text{(Quadrieren)} \\[0.8em] x &= \frac{1}{9}\end{align*}\]
oder
\[\begin{align*} f(x) &= 0 \\[0.8em] 2\ln{\left(3\sqrt{x}\right)} &= 0 & &| \; n \cdot \log_{a}{x} = \log_{a}\left( x^{n} \right) \\[0.8em] \ln{\left(3\sqrt{x}\right)^{2}} &= 0 \\[0.8em] \ln{9x} &= 0 &&| \; \ln{1} = 0 \\[0.8em] 9x &= 1 &&| : 9 \\[0.8em] x &= \frac{1}{9}\end{align*}\]
oder
\[\begin{align*} f(x) &= 0 \\[0.8em] 2\ln{\left(3\sqrt{x}\right)} &= 0 & &| \; n \cdot \log_{a}{x} = \log_{a}\left( x^{n} \right) \\[0.8em] \ln{\left(3\sqrt{x}\right)^{2}} &= 0 \\[0.8em] \ln{9x} &= 0 &&| \; e^{(\dots)} \; \text{(zur Basis}\; e \; \text{potenzieren)} \\[0.8em] e^{\ln{9x}} &= e^{0} &&| \; e^{\ln{x}} = x; \; \left( \text{allg.:} \; a^{\log_{a}{x}} = x \right), a^{0} = 1; \; \text{hier:} \; e^{0} = 1 \\[0.8em] 9x &= 1 &&| : 9 \\[0.8em] x &= \frac{1}{9}\end{align*}\]
Die Funktion \(f\) besitzt die einzige Nullstelle \(x = \frac{1}{9}\).
Ableitungsfunktion \(f'\) der Funktion \(f\)
Die Funktion \(f\) wird mithilfe der Ableitung der natürlichen Logarithmusfunktion, der Ableitung einer Wurzelfunktion, der Kettenregel und der Faktorregel abgeleitet. Als Alternative lässt sich der Funktionsterm \(f(x)\) unter Anwendung der Rechenregel für Logarithmen \(\log_{a}{b^{n}} = n \cdot \log_{a}{b}\) vorab wurzelfrei formulieren.
\[f(x) = 2\ln{3\sqrt{x}} = \ln{\left( 3\sqrt{x} \right)^{2}} = \ln{9x}\]
1. Möglichkeit: Ohne Umformulieren von \(f(x)\)
\[f(x) = 2\ln{3\sqrt{x}}\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung der natürlichen Logarithmusfunktion
\[f(x) = \ln x \enspace (x > 0) \quad \Longrightarrow \quad f'(x) = \frac{1}{x}\]
Ableitung einer Wurzelfunktion
\[f(x) = \sqrt{g(x)} \quad \Longrightarrow \quad f'(x) = \frac{g'(x)}{2\sqrt{g(x)}} \quad (g(x) \geq 0)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
(vgl. Merkhilfe)
\[\left[u(v(x))\right]' = u'(v(x)) \cdot v'(x)\]
\[u(x) = 2\ln{x}; \; u'(x) = 2 \cdot \frac{1}{x}\]
\[v(x) = 3\sqrt{x}; \; v'(x) = 3 \cdot \frac{1}{2\sqrt{x}}\]
\[f'(x) = 2 \cdot \frac{1}{3\sqrt{x}} \cdot 3 \cdot \frac{1}{2\sqrt{x}} = \frac{1}{x}\]
2. Möglichkeit: Nach Umformulieren von \(f(x)\)
\[f(x) = \ln{9x}\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung der natürlichen Logarithmusfunktion
\[f(x) = \ln x \enspace (x > 0) \quad \Longrightarrow \quad f'(x) = \frac{1}{x}\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\left[u(v(x))\right]' = u'(v(x)) \cdot v'(x)\]
\[u(x) = \ln{x}; \; u'(x) = \frac{1}{x}\]
\[v(x) = 9x; \; v'(x) = 9\]
\[f'(x) = \frac{1}{9x} \cdot 9 = \frac{1}{x}\]
b) Funktion \(g(x) = xe^{4 - 3x} + \dfrac{x^{2}}{e^{3x - 4}}\)
Maximale Definitionsmenge der Funktion \(g\)
Die natürliche Exponentialfunktion \(x \mapsto e^{x}\) ist in \(\mathbb R\) definiert und besitzt den Wertebereich \(\mathbb R^{+}\). Der Exponent \(4 - 3x\) beeinflusst weder den Definitions- noch den Wertebereich. (vgl. Abiturskript - 1.3.1 Eigenschaften und Rechenregeln, Natürliche Exponential- und Logarithmusfunktion). Die Terme \(x\) und \(x^{2}\) sind ebenfalls in \(\mathbb R\) definiert.
\[\Longrightarrow \quad D_{g} = \mathbb R\]
Nullstelle(n) der Funktion g
\[g(x) = xe^{4 - 3x} + \dfrac{x^{2}}{e^{3x - 4}}\]
Die Funktion \(g\) kann mithilfe der Rechenregel für Potenzen \(a^{-n} = \frac{1}{a^{n}}\) in ein Produkt umgeformt werden. Anschließend lässt sich der Satz vom Nullprodukt anwenden.
\[\begin{align*} g(x) &= xe^{4 - 3x} + \frac{x^{2}}{e^{3x - 4}} \\[0.8em] &= xe^{4 - 3x} + \frac{x^{2}}{e^{-(4 - 3x)}} &&| \; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= xe^{4 - 3x} + \frac{x^{2}}{\frac{1}{e^{4 - 3x}}} &&| \; x^{2} \;\text{mit Kehrbruch}\; \frac{e^{4 - 3x}}{1}\; \text{multiplizieren} \\[0.8em] &= xe^{4 - 3x} + x^{2}e^{4 - 3x} &&| \; \text{Faktor}\; e^{4 - 3x}\;\text{ausklammern} \\[0.8em] &= e^{4 - 3x}(x^{2} + x) \end{align*}\]
\[\begin{align*} g(x) &= 0 \\[0.8em] e^{4 - 3x} \cdot (x^{2} + x) &= 0 \\[0.8em] \underbrace{e^{4 - 3x}}_{>\,0} \cdot x \cdot (x + 1) &= 0 \end{align*}\]
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).
Satz vom Nullprodukt:
Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist.
\[\Longrightarrow \quad x = 0 \enspace \vee \enspace x + 1 = 0 \Leftrightarrow x = -1\]
Die Funktion \(g\) besitzt die Nullstellen \(x_{1} = -1\) und \(x_{2} = 0\).
Ableitungsfunktion \(g'\) der Funktion \(g\)
Den ursprünglichen Funktionsterm \(g(x) = xe^{4 - 3x} + \dfrac{x^{2}}{e^{3x - 4}}\) mithilfe der Produkt- und der Quotientenregel abzuleiten und anschließend zu vereinfachen, ist relativ aufwendig. Zeitsparender ist es, den Funktionsterm \(g(x) = e^{4 - 3x}(x^{x} + x)\) (vgl. Nullstellen von \(g\)) mithilfe der Produktregel sowie der Kettenregel, der Ableitung der natürlichen Exponentialfunktion, der Ableitung einer Potenzfunktion, der Summenregel und der Faktorregel abzuleiten.
\[g(x) = e^{4 - 3x}(x^{2} + x)\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\left[u(x) \cdot v(x)\right]' = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
\[u(x) = e^{4 - 3x}; \; u'(x) = e^{4 - 3x} \cdot (-3)\]
\[v(x) = x^{2} + x; \; v'(x) = 2x + 1\]
\[\begin{align*}g'(x) &= e^{4 - 3x} \cdot (-3) \cdot (x^{2} + x) + e^{4 - 3x} \cdot (2x + 1) &&| \; \text{Faktor}\; e^{4 - 3x}\; \text{ausklammern} \\[0.8em] &= e^{4 - 3x} (- 3x^{2} - 3x + 2x + 1) \\[0.8em] &= e^{4 - 3x}(-3x^{2} - x + 1) \end{align*}\]
c) Funktion \(h(x) = x^{3} \cdot \sin{\left( \dfrac{\pi}{3}x \right)}\)
Maximale Definitionsmenge der Funktion \(h\)
Die Funktion \(h\) ist das Produkt der beiden in \(\mathbb R\) definierten Funktionen \(x \mapsto x^{3}\) und \(x \mapsto \sin{\left( \frac{\pi}{3}x \right)}\).
\[\Longrightarrow \quad D_{h} = \mathbb R\]
Nullstelle(n) der Funktion \(h\)
\[\begin{align*} h(x) &= 0 \\[0.8em] x^{3} \cdot \sin{\left( \frac{\pi}{3}x \right)} &= 0 \end{align*}\]
Satz vom Nullprodukt:
Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist.
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).
\[x^{3} = 0 \Leftrightarrow x = 0 \enspace \vee \enspace \sin{\left( \frac{\pi}{3}x \right)} = 0\]
Die Nullstellen der Sinusfunktion \(x \mapsto \sin{x}\) sind \(x = k\pi\) mit \(k \in \mathbb Z\). Folglich muss \(\dfrac{\pi}{3}x = k\pi\) gelten.
\[\begin{align*} \frac{\pi}{3}x &= k\pi &&| : \pi \\[0.8em] \frac{x}{3} &= k &&| \cdot 3 \\[0.8em] x &= 3k \end{align*}\]
Die Funktion h besitzt die Nullstellen \(x = 3k\) mit \(k \in \mathbb Z\).
Anmerkung:
Die Nullstelle \(x = 0\) von \(x^{3} = 0\) (dreifache Nullstelle) ist mit \(k = 0\) ebenfalls eine Nullstelle von \(\sin{\left(\dfrac{\pi}{3}x\right)} = 0\) und somit eine vierfache Nullstelle der Funktion \(h\).
Ableitungsfunktion \(h'\) der Funktion \(h\)
Die Funktion \(h\) lässt sich mithilfe der Produktregel, der Kettenregel, der Ableitung der Sinusfunktion, der Ableitung einer Potenzfzunktion sowie der Faktorregel ableiten.
\[h(x) = x^{3} \cdot \sin{\left( \dfrac{\pi}{3}x \right)}\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung der Sinusfunktion
\[ f(x) = \sin x \quad \Longrightarrow \quad f'(x) = \cos x\]
Ableitung einer Potenzfunktion
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
(vgl. Merkhilfe)
\[\left[u(x) \cdot v(x)\right]' = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
\[u(x) = x^{3}; \; u'(x) = 3x^{2}\]
\[v(x) = \sin{\left( \dfrac{\pi}{3}x \right)}; \; v'(x) = \cos{\left( \dfrac{\pi}{3}x \right)} \cdot \dfrac{\pi}{3}\]
\[\begin{align*} h'(x) &= 3x^{2} \cdot \sin{\left( \frac{\pi}{3}x \right)} + x^{3} \cdot \cos{\left( \frac{\pi}{3}x \right)} \cdot \frac{\pi}{3} \\[0.8em] &= \frac{1}{3}x^{2}\left[ 9\sin{\left( \frac{\pi}{3}x \right)} + \pi x \cos{\left( \frac{\pi}{3}x \right)} \right] \end{align*}\]

