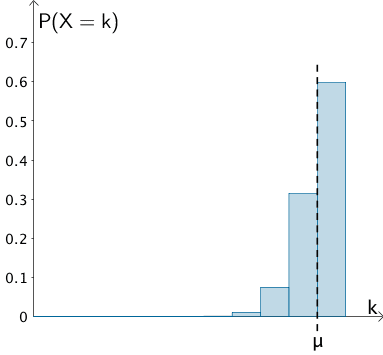
Die Abbildung zeigt die vollständige Wahrscheinlichkeitsverteilung einer nach \(B(n;p)\) binomialverteilten Zufallsgröße \(X\) und kennzeichnet die Lage des Erwartungswerts \(\mu = E(X)\).
Bestimmen Sie mithilfe der Abbildung und unter Verwendung des Stochastischen Tafelwerks die Werte der Parameter \(n\) und \(p\). Erläutern Sie Ihre Vorgehensweise.
Die Abbildung zeigt die Wahrscheinlichkeitsverteilung einer nach \(B(10;0{,}95)\) binomialverteilten Zufallsgröße \(X\).
Erläuterung der Vorgehensweise:
Die Abbildung zeigt die Wahrscheinlichkeitsverteilung einer nach \(B(n;p)\) binomialverteilten Zufallsgröße \(X\), deren Erwartungswert \(\mu = E(X)\) - und damit das Maximum der Binomialverteilung - hin zu großen Trefferanzahlen \(k\) verschoben ist. Daraus lässt sich schließen, dass \(p > 0{,}5\) gelten muss (vgl. Abiturskript - 3.3.3 Binomialverteilte Zufallsgröße, Histogramme einer Binomialverteilung). Wegen der sehr ausgeprägten Verschiebung hin zu großen Trefferanzahlen, darf eine Trefferwahrscheinlichkeit \(p\) angenommen werden, die deutlich größer als \(0{,}5\) ist.
Die Wahrscheinlichkeit dafür, dass die Zufallsgröße \(X\) einen Wert \(X > \mu\) annimmt, beträgt gemäß der Abbildung ca. \(0{,}6\). Da die Summe der Wahrscheinlichkeiten aller Trefferanzahlen gleich Eins ist \((\sum \limits_{i\,=\,0}^{k = n}B(n:p;i) = 1)\), finden sich hohe Wahrscheinlichkeiten \(P(X = k) > 0{,}5\) für Bernoulliketten kleiner Längen \(n\).
Der Darstellung der Balken in der Abbildung zufolge, kann \(n = 10\) angenommen werden, wobei jede Wahrscheinlichkeit \(P(X = k)\) für \(k \leq 6\) nahezu gleich Null ist.
Erwartungswert \(\boldsymbol{\mu}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\(\mu = E(X) = n \cdot p\) (vgl. Merkhilfe)
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist.
Sei also beispielsweise \(p = 0{,}9\) und \(n = 10\) angenommen, so ergibt sich der Erwartungswert zu \(\mu = n \cdot p = 10 \cdot 0{,}9 = 9\). Dann müsste \(P(X > \mu) = P(X = 10) \approx 0{,}6\) gelten. Dem Stochastischen Tafelwerk (ST) entnimmt man mit \(P_{0{,}9}^{10}(X = 10) \overset{\text{ST}}{=} 0{,}34868\), dass dies nicht der Fall ist. Folglich muss \(p > 0{,}9\) gelten. Außerdem zeigt die Abbildung, dass der Erwartungswert \(\mu\) kein ganzzahliger Wert ist, den die Zufallsgröße \(X\) annehmen kann.
Die nächstgrößere im Stochstischen Tafelwerk tabellarisierte Trefferwahrscheinlichkeit ist \(p = 0{,}95\). Dann gilt \(\mu = 10 \cdot 0{,}95 = 9{,}5\).
Mit \(P_{0{,}95}^{10}(X > \mu) = P_{0{,}95}^{10}(X = 10) \overset{\text{ST}}{=} 0{,}59874\) und außerdem \(P_{0{,}95}^{10}(X = 9) \overset{\text{ST}}{=} 0{,}31512\) ergibt sich eine klare Übereinstimmung mit der abgebildeten Wahrscheinlichkeitsverteilung.

