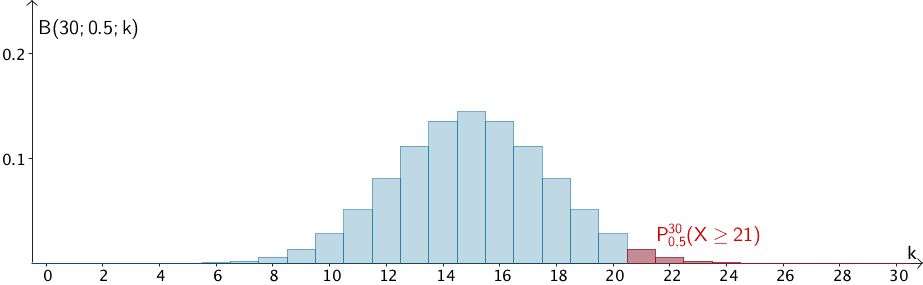
Die Schulleitung fordert, den Vortest so zu gestalten, dass die Wahrscheinlichkeit dafür, den Vortest zu bestehen, für einen Bewerber, der nur rät, höchstens 3 % beträgt. Man entscheidet sich dafür, die Anzahl vorgelegter Schriftproben auf 30 festzulegen.
Zeigen Sie, dass mit dieser Festlegung die Forderung der Schulleitung erfüllt ist.
(3 BE)
Lösung zu Teilaufgabe 1b
Zufallsgröße \(X \colon \enspace\)„Anzahl der richtig beurteilten Schriftproben"
Analyse der Angabe:
"... die Anzahl vorgelegter Stichproben auf 30 zu erhöhen ..."
\[\Longrightarrow \quad n = 30\]
"... ratender Bewerber ...", siehe Teilaufgabe 1a
\[\Longrightarrow \quad p = 0{,}5\]
"... bei mehr als zwei Drittel eine richtige Entscheidung ..."
\[\frac{2}{3} \cdot 30 = 20 \quad \Longrightarrow \quad X \geq 21\]
Binomialverteilung
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
Die Zufallsgröße \(X\) ist nach \(B(30;0{,}5)\) binomialverteilt.
Betrachten des Gegenereignisses:
Betrachten des Gegenereignisses (mindestens \(k\) Treffer)
Kumulative Wahrscheinlichkeiten der Form \(P(X \geq k)\) lassen sich im Stochastischen Tafelwerk (ST) nicht nachschlagen. Die Betrachtung des Gegenereignisses ermöglicht das Verwenden des Stochastischen Tafelwerks:
\[P(X \geq k) = 1 - P(X \leq k - 1)\]
Die Kumulative Verteilungsfunktion \(F_{p}^{n}(k) = P^n_p(X \leq k) = \sum \limits_{i\;=\;0}^{k} B(n;p;i)\) ist für bestimmte Werte der Parameter \(p\) und \(n\) in der rechten Spalte des Stochastischen Tafelwerks mit Abiturzulassung tabellarisiert.
\[P^{30}_{0{,}5}(X \geq 21) = 1 - P^{30}_{0{,}5}(X \leq 20)\]
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
Stochastisches Tafelwerk (ST) verwenden:
\[F^{30}_{0{,}5} (20) = P^{30}_{0{,}5} (X \leq 20) = \sum \limits_{i \, = \, 0}^{20} B(30; 0{,}5; i) \enspace \overset{\text{ST}}{=} \enspace 0{,}97861\]
\[\begin{align*}P^{30}_{0{,}5}(X \geq 21) &= 1 - 0{,}97861 \\[0.8em] &= 0{,}02139 \approx 2{,}1 \; \% \end{align*}\]
Mit 2,1 % liegt die Wahrscheinlichkeit dafür, dass ein nur ratender Bewerber den Vortest besteht, unter 3 %. Damit erfüllt die Festlegung auf 30 Schriftproben die Forderung der Schulleitung.