In einen leeren Behälter werden drei Kugeln gelegt. Dabei wird die Farbe jeder Kugel durch Werfen eines Würfels festgelegt, dessen Seiten mit den Zahlen 1 bis 6 durchnummeriert sind: Wird die „1" oder die „2" erzielt, wird eine gelbe Kugel gewählt, sonst eine schwarze.
Weisen Sie rechnerisch nach, dass die Wahrscheinlichkeit dafür, dass sich nun mindestens zwei schwarze Kugeln im Behälter befinden, \(\large{\frac{20}{27}}\) beträgt.
(2 BE)
Lösung zu Teilaufgabe a
Zwei mögliche rechnerische Nachweise:
\[\begin{align*}&\quad \; \, P(\text{„mindestens 2 schwarze Kugeln"}) =\\[0.8em] &= \frac{1}{3} \cdot \frac{2}{3} \cdot \frac{2}{3} + \frac{2}{3} \cdot \frac{1}{3} \cdot \frac{2}{3} + \frac{2}{3} \cdot \frac{2}{3} \cdot \frac{1}{3} + \frac{2}{3} \cdot \frac{2}{3} \cdot \frac{2}{3} \\[0.8em] &= 3 \cdot \frac{1}{3} \cdot \left( \frac{2}{3} \right)^2 + \left( \frac{2}{3} \right)^3 = \frac{12}{27} + \frac{8}{27} = \frac{20}{27} \end{align*}\]
\[\begin{align*}&\quad \; \, P(\text{„mindestens 2 schwarze Kugeln"}) = \\[0.8em] &= \binom{3}{2} \cdot \left( \frac{2}{3} \right)^2 \cdot \frac{1}{3} + \binom{3}{3} \cdot \left( \frac{2}{3} \right)^3 \cdot \left(\frac{1}{3}\right)^0 \\[0.8em] &= 3 \cdot \left( \frac{2}{3} \right)^2 \cdot \frac{1}{3} + \left( \frac{2}{3} \right)^3 = \frac{12}{27} + \frac{8}{27} = \frac{20}{27}\end{align*}\]
Ausführliche Erklärung (nicht verlangt)
Es werden die Ereignisse
\(g\): „Es wird eine gelbe Kugel in den Behälter gelegt."
\(s\): „Es wird eine schwarze Kugel in den Behälter gelegt."
betrachtet.
Eine „1" oder eine „2" wird mit der Wahrscheinlichkeit \(\dfrac{2}{6} = \dfrac{1}{3}\) gewürfelt.
\[\Rightarrow \enspace P(g) = \frac{1}{3}; \; P(s) = \frac{2}{3}\]
Veranschaulichung mithilfe eines Baumdiagramms:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
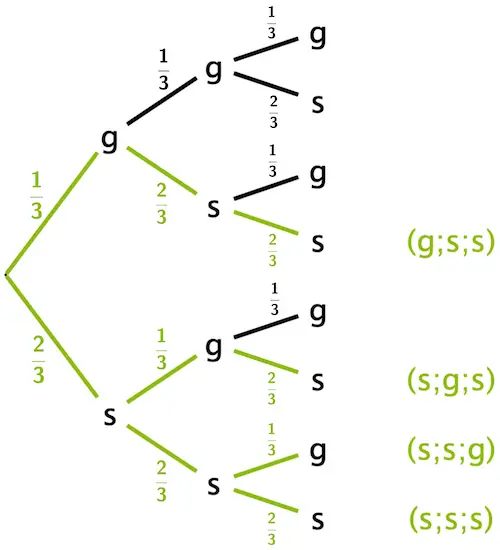
Mithilfe der 1. und der 2. Pfadregel ergibt sich:
\[\begin{align*}&\quad \; \, P(\text{„mindestens 2 schwarze Kugeln"}) = \\[0.8em] &= P(\{\textcolor{#89ba17}{(g;s;s)}\}) + P(\{\textcolor{#89ba17}{(s;g;s)}\}) + P(\{\textcolor{#89ba17}{(s;s;g)}\}) + P(\{\textcolor{#89ba17}{(s;s;s)}\}) \\[0.8em] &= \underbrace{\underbrace{\textcolor{#89ba17}{\frac{1}{3}} \cdot \textcolor{#89ba17}{\frac{2}{3}} \cdot \textcolor{#89ba17}{\frac{2}{3}}}_{\text{1. Pfadregel}} + \underbrace{\textcolor{#89ba17}{\frac{2}{3}} \cdot \textcolor{#89ba17}{\frac{1}{3}} \cdot \textcolor{#89ba17}{\frac{2}{3}}}_{\text{1. Pfadregel}} + \underbrace{\textcolor{#89ba17}{\frac{2}{3}} \cdot \textcolor{#89ba17}{\frac{2}{3}} \cdot \textcolor{#89ba17}{\frac{1}{3}}}_{\text{1- Pfadregel}} + \underbrace{\textcolor{#89ba17}{\frac{2}{3}} \cdot \textcolor{#89ba17}{\frac{2}{3}} \cdot \textcolor{#89ba17}{\frac{2}{3}}}_{\text{1. Pfadregel}}}_{\text{2. Pfadregel}} \\[0.8em] &= 3 \cdot \frac{1}{3} \cdot \left( \frac{2}{3} \right)^2 + \left( \frac{2}{3} \right)^3 = \frac{12}{27} + \frac{8}{27} = \frac{20}{27} \end{align*}\]
Das Zufallsexperiment lässt sich auch als Bernoulli-Kette der Länge \(\textcolor{#0087c1}{n = 3}\) auffassen.
Bernoulli-Experiment, Bernoulli-Kette
Ein Zufallsexperiment, bei dem nur zwei verschiedene sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können, heißt Bernoulli-Experiment.
Das Eintreten des Ereignisses \(A\) wird als Treffer und das Eintreten des Gegeneignisses \(\overline{A}\) wird als Niete bezeichnet. Die Trefferwahrscheinlichkeit \(P(A)\) bezeichnet man mit \(\boldsymbol{p}\) und die Wahrscheinlichkeit für eine Niete mit \(q = 1- p\). Wird ein Bernoulli-Experiment \(n\)-mal wiederholt, spricht man von einer Bernoulli-Kette der Länge \(\boldsymbol{n}\). Dabei müssen die einzelnen Wiederholungen unabhängig voneinander erfolgen. Das heißt, die Trefferwahrscheinlichkeit \(p\) bleibt konstant.
Betrachtet wird das Ereignis „Es wird eine schwarze Kugel in den Behälter gelegt" mit der Trefferwahrscheinlichkeit \(\textcolor{#cc071e}{p} = P(s) \textcolor{#cc071e}{= \dfrac{2}{3}}\).
Es sei \(X\) die Zufallsgröße, welche die Anzahl der schwarzen Kugeln im Behälter beschreibt.
Die Zufallsgröße \(X\) ist nach \(B\big(\textcolor{#0087c1}{3};\textcolor{#cc071e}{\frac{2}{3}}\big)\) binomialverteilt.
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
\[\begin{align*}&\quad \; \, P(\text{„mindestens 2 schwarze Kugeln"}) = P_{\textcolor{#cc071e}{\frac{2}{3}}}^{\textcolor{#0087c1}{3}}(\textcolor{#e9b517}{X \geq 2}) \\[0.8em] &= P_{\textcolor{#cc071e}{\frac{2}{3}}}^{\textcolor{#0087c1}{3}}(\textcolor{#e9b517}{X = 2}) + P_{\textcolor{#cc071e}{\frac{2}{3}}}^{\textcolor{#0087c1}{3}}(\textcolor{#e9b517}{X = 3}) \\[0.8em] &= \binom{\textcolor{#0087c1}{3}}{\textcolor{#e9b517}{2}} \cdot \left( \textcolor{#cc071e}{\frac{2}{3}} \right)^{\textcolor{#e9b517}{2}} \cdot \left(1 -\textcolor{#cc071e}{\frac{2}{3}}\right)^{\textcolor{#0087c1}{3} \,-\, \textcolor{#e9b517}{2}} + \binom{\textcolor{#0087c1}{3}}{\textcolor{#e9b517}{3}} \cdot \left( \textcolor{#cc071e}{\frac{2}{3}} \right)^{\textcolor{#e9b517}{3}} \cdot \left(1 -\textcolor{#cc071e}{\frac{2}{3}}\right)^{\textcolor{#0087c1}{3} \,-\, \textcolor{#e9b517}{3}} &&| \; \binom{n}{k = n} = 1 \\[0.8em] &= 3 \cdot \left( \frac{2}{3} \right)^2 \cdot \frac{1}{3} + 1 \cdot \left( \frac{2}{3} \right)^3 \cdot \left( \frac{1}{3} \right)^0 &&|\; a^0 = 1 \\[0.8em] &= \frac{12}{27} + \frac{8}{27} = \frac{20}{27}\end{align*}\]


