Geben Sie die Koordinaten eines weiteren Punkts \(D\) der \(x_{2}\)-Achse an, so dass das Dreieck \(ABD\) bei \(D\) rechtwinklig ist. Begründen Sie Ihre Antwort.
(2 BE)
Lösung zu Teilaufgabe 1b
Spiegelung (eines Punktes) an einer Ebene, Umkreis eines rechtwinkligen Dreiecks (Thaleskreis)
\(A(2|3|1)\), \(B(2|-3|1)\), \(C(0|2|0)\)
Der Punkt \(D(0|-2|0)\) liegt auf der \(x_{2}\)-Achse, sodass das Dreieck \(ABD\) bei \(D\) rechtwinklig ist.
Begründung:
Die Punkte \(A\) und \(B\) sind zueinander Ur- und Bildpunkte, die durch Spiegelung an der \(x_{1}x_{3}\)-Ebene hervorgehen. Der Punkt \(D(0|-2|0)\) geht aus dem Punkt \(C(0|2|0)\) ebenfalls durch Spiegelung an der \(x_{1}x_{3}\)-Ebene hervor. Damit wird das Dreieck \(ABC\) vollständig durch Spiegelung an der \(x_{1}x_{3}\)-Ebene auf das Dreieck \(ABD\) abgebildet. Die Spiegelung ist eine Kongruenzabbildung, was bedeutet, dass der rechte Winkel bei \(C\) des Dreiecks \(ABC\) erhalten bleibt (Winkeltreue). Somit ist das Dreieck \(ABD\) bei \(D\) rechtwinklig.
Rechnerische Begründung:
Mithilfe des Skalarprodukts wird durch Rechnung bestätigt, dass das Dreieck \(ABD\) bei Punkt \(D(0|-2|0)\) rechtwinklig ist.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{DA} \circ \overrightarrow{DB} = 0 \quad \Longleftrightarrow \quad \overrightarrow{DA} \perp \overrightarrow{DB}\]
Verbindungsvektoren \(\overrightarrow{DA}\) und \(\overrightarrow{DB}\) berechnen:
\(A(2|3|1)\), \(B(2|-3|1)\), \(D(0|-2|0)\)
\[\overrightarrow{DA} = \overrightarrow{A} - \overrightarrow{D} = \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix} - \begin{pmatrix} 0 \\ -2 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 5 \\ 1 \end{pmatrix}\]
\[\overrightarrow{DB} = \overrightarrow{B} - \overrightarrow{D} = \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix} - \begin{pmatrix} 0 \\ -2 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}\]
Skalarprodukt orthogonaler (senkrechter) Vektoren anwenden:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \overrightarrow{DA} \circ \overrightarrow{DB} &= \begin{pmatrix} 2 \\ 5 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} \\[0.8em] &= 2 \cdot 2 + 5 \cdot (-1) + 1 \cdot 1 \\[0.8em] &= 0 \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{DA} \perp \overrightarrow{DB}\]
\(\Longrightarrow \quad\)Das Dreieck \(ABD\) ist bei \(D\) rechtwinklig.
Alternative Begründung:
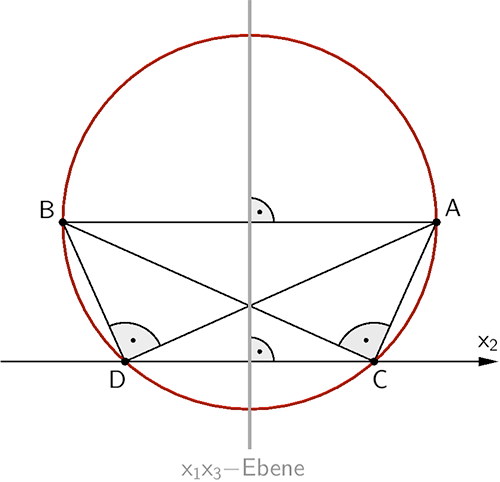
Planskizze: Aufsicht auf die Ebene, in der das Dreieck \(ABC\) liegt.
Das Dreieck \(ABC\) ist bei \(C\) rechtwinklig (vgl. Teilaufgabe 1a). Die Punkte \(A\) und \(B\) sind bezüglich der \(x_{1}x_{3}\)-Ebene symmetrisch (vgl. Angabe Aufgabe 1). Der Punkt \(C(0|2|0)\) liegt auf der \(x_{2}\)-Achse.
Satz des Thales
Liegt der Punkt \(C\) eines Dreiecks \(ABC\) auf einem Kreis mit dem Durchmesser \([AB]\), ist der Winkel bei Punkt \(C\) ein rechter Winkel.
Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt immer in der Mitte der Hypotenuse.
Der Umkreis des rechtwinkligen Dreiecks \(ABC\) ist der Thaleskreis mit dem Durchmesser \([AB]\). Der Punkt \(D(0|-2|0)\) geht durch Spiegelung des Punktes \(C\) an der \(x_{1}x_{3}\)-Ebene hervor. Er liegt auf der \(x_{2}\)-Achse und ebenfalls auf dem Thaleskreis.
Folglich ist das Dreieck \(ABD\) bei \(D\) rechtwinklig.


