Beschreiben Sie, wie \(G_{g}\) schrittweise aus dem Graphen der in \(\mathbb R^{+}_{0}\) definierten Funktion \(w \colon x \mapsto \sqrt{x}\) hervorgeht, und geben Sie die Wertemenge von \(g\) an.
(4 BE)
Lösung zu Teilaufgabe 1b
Entwicklung von Funktionen, Wertemenge einer Funktion
\[w(x) = \sqrt{x}; \; D_{w} = \mathbb R_{0}^{+}\]
\[g(x) = 2 \cdot \sqrt{4 + x} - 1; \; D_{g} = [-4;+\infty[\]
Schrittweise Entstehung von \(G_{g}\) aus \(G_{w}\)
Um die Entstehung des Graphen der Funktion \(g\) aus dem Graphen der Funktion \(w\) zu beschreiben, wird der Funktionsterm \(g(x) = 2 \cdot \sqrt{4 + x} - 1\) „von innen nach außen" betrachtet.
Wie wirkt sich der lineare Term \(4 + x\) im Argument der Funktion \(w(x) = \sqrt{x}\) auf den Graphen von \(w\) aus?
Wie wirkt sich der Faktor 2 vor der Wurzel aus (Punkt vor Strich beachten)?
Wie wirkt sich der Subtrahend 1 aus?
1. Verschiebung um vier Einheiten in negative \(x\)-Richtung:
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[w(x + 4) = \sqrt{x + 4} = \sqrt{4 + x}\]
2. Streckung in \(y\)-Richtung mit dem Faktor 2:
Strecken von Funktionsgraphen
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{k}\,\):
\[h(x) = f\left(\textcolor{#0087c1}{\frac{1}{k}} \cdot x \right), \enspace k > 0\]
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{\dfrac{1}{k}}\):
\[h(x) = f(\textcolor{#0087c1}{k} \cdot x), \enspace k > 0\]
Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit Streckungsfaktor \(\textcolor{#cc071e}{k}\,\):
\[g(x) = \textcolor{#cc071e}{k} \cdot f(x), \enspace k > 0\]
\[2 \cdot w(x + 4) = 2 \cdot \sqrt{4 + x}\]
3. Verschiebung um eine Einheit in negative \(y\)-Richtung:
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[2 \cdot w(x + 4) - 1 = 2 \cdot \sqrt{4 + x} - 1 = g(x)\]
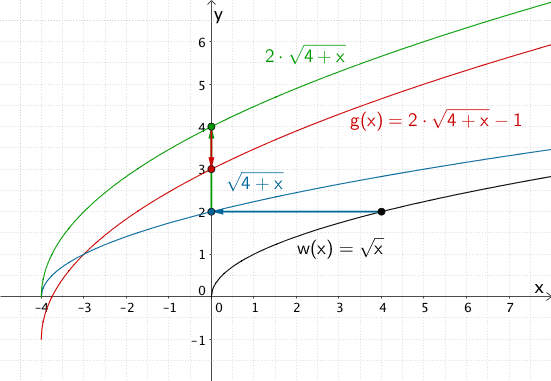
Entstehung des Graphen der Funktion \(g \colon x \mapsto 2 \cdot \sqrt{4 + x} - 1\) mit \(D_{g} = [-4;+\infty[\) aus dem Graphen der in \(\mathbb R_{0}^{+}\) definierten Funktion \(w \colon x \mapsto \sqrt{x}\)
Wertemenge von \(g\)
Von den genannten Schritten der Entstehung von \(G_{g}\) aus dem Graphen der Funktion \(w\) wirkt sich nur die Verschiebung um eine Einheit in negative \(y\)-Richtung (3. Schritt) auf die Wertemenge der Funktion \(g\) aus.
\[w(x) = \sqrt{x}\]
Der Wert einer Wurzel ist größer oder gleich Null.
\[W_{w} = \mathbb R_{0}^{+} = [0;+\infty[\]
Verschiebung um eine Einheit in negative \(y\)-Richtung:
\[\Longrightarrow \quad W_{g} = [-1;+\infty[\]
Anmerkung:
Die Wertemenge \(W_{g}\) muss nur angegeben werden (vgl. Angabe). jede Erklärung kann entfallen.


