Begründen Sie, dass die Größe des Schnittwinkels von \(g_k\) und der \(x_1x_2\)-Ebene weniger als 30° beträgt, wenn \(2k^2 > 1\) gilt.
(5 BE)
Lösung zu Teilaufgabe d
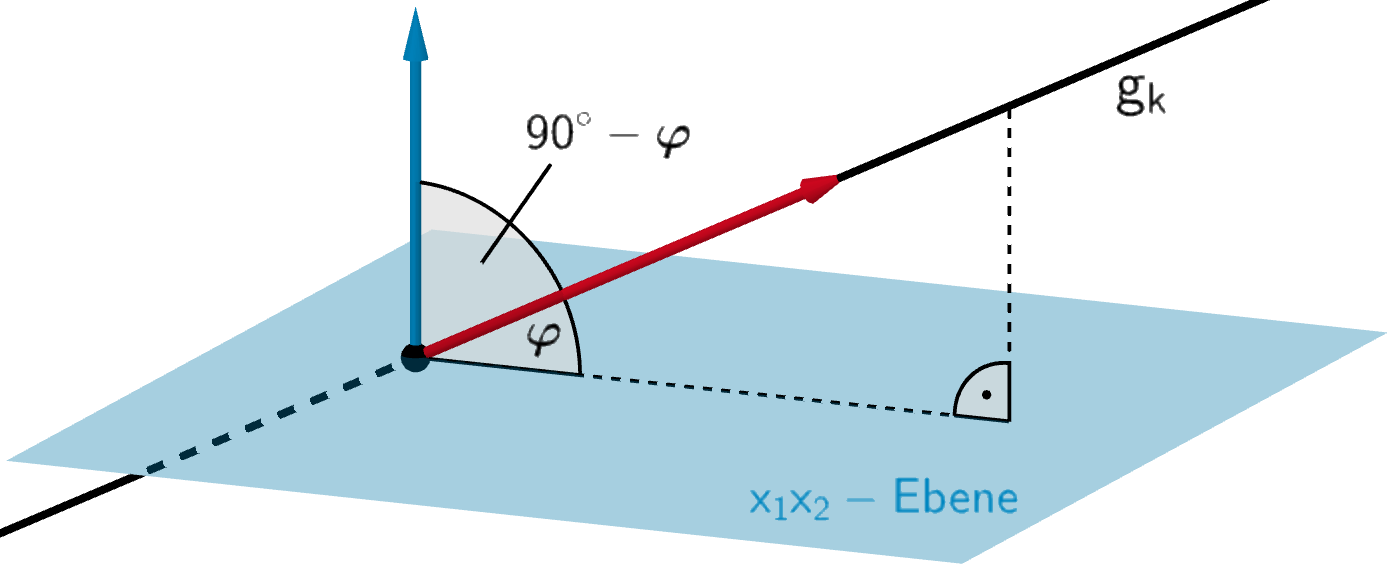
Schnittwinkel \(\varphi\) zwischen \(g_k\) und der \(x_1x_2\)-Ebene (schematische Darstellung)
Es gilt die Komplementbeziehung \(\cos{(90^{\circ} - \varphi)} = \sin{\varphi}\).
\(\textcolor{#0087c1}{\begin{pmatrix} 0\\0\\1 \end{pmatrix}}\) ist ein Normalenvektor der \(\textcolor{#0087c1}{x_1x_2}\)-Ebene.
\[g_k \colon \overrightarrow{X} = \begin{pmatrix} 0\\0\\10 \end{pmatrix} + \lambda \cdot \textcolor{#cc071e}{\begin{pmatrix} 1+k\\1-k\\-1 \end{pmatrix}}, \; \lambda \in \mathbb R\]
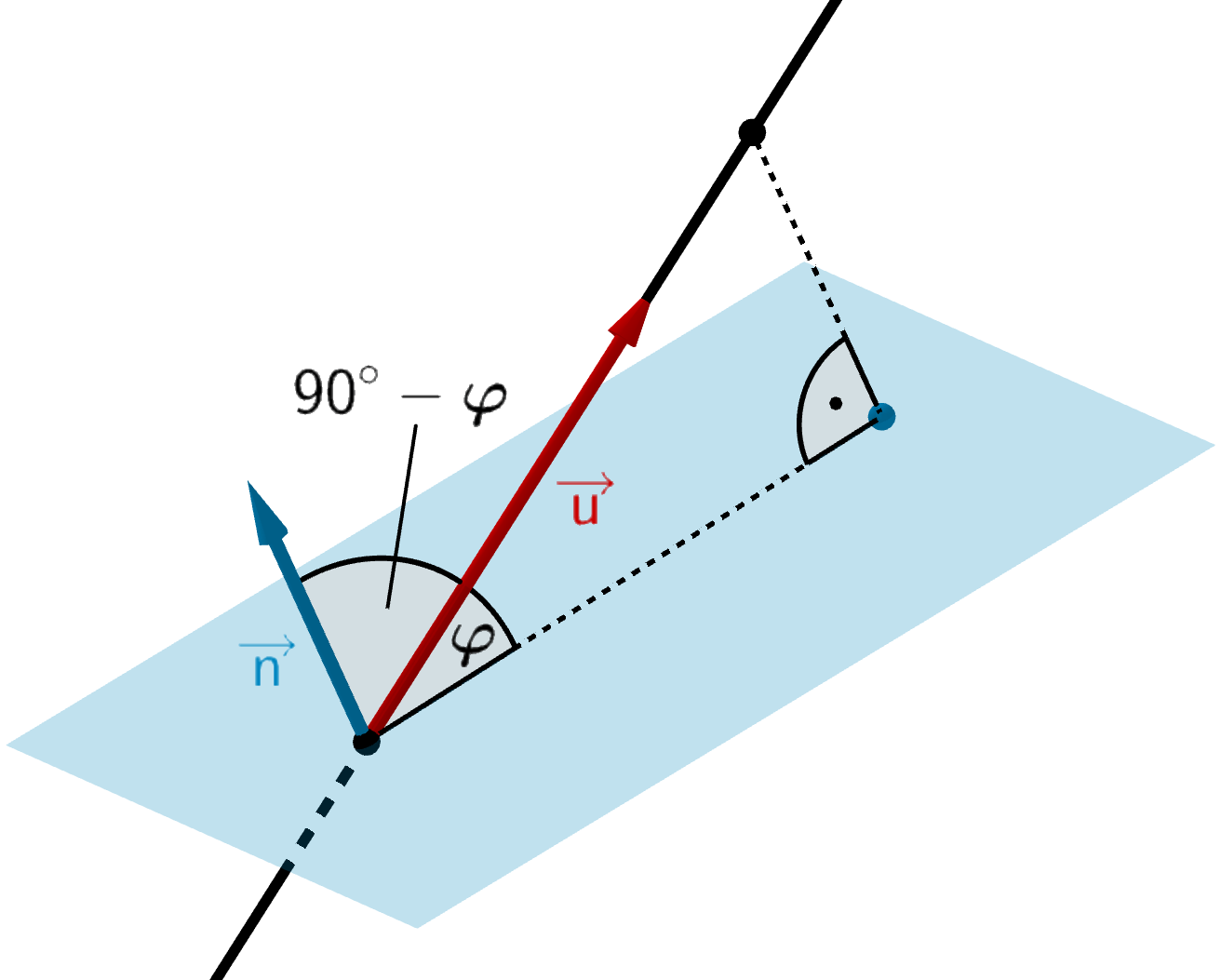
Schnittwinkel \(\boldsymbol{\varphi}\) zwischen Gerade und Ebene
\[\cos{(90^{\circ} - \varphi)} = \frac{\vert \textcolor{#cc071e}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{n}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{u}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{n}} \vert}\]
Mit \(\cos{(90^{\circ}-\varphi)} = \sin{\varphi}\) folgt:
\[\begin{align*}\sin{\varphi} &= \frac{\vert \textcolor{#cc071e}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{n}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{u}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{n}} \vert} = \cdots \quad(0^{\circ} \leq \varphi \leq 90^{\circ}) \\[0.8em] \varphi &= \sin^{-1}(\cdots)\end{align*}\]
\begin{align*} \sin{\varphi} = \cos{(90^{\circ} - \varphi)} &= \frac{\left|\textcolor{#cc071e}{\begin{pmatrix} k+1 \\ k-1 \\ -1 \end{pmatrix}} \circ \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}}\right|}{\left| \textcolor{#cc071e}{\begin {pmatrix} k+1 \\ k-1 \\ -1 \end {pmatrix}} \right| \cdot \left| \textcolor{#0087c1}{\begin {pmatrix} 0 \\ 0 \\ 1 \end {pmatrix}} \right|} \\[0.8em] &= \frac{\vert -1 \vert}{\sqrt{(k+1)^2 + (k-1)^2 + (-1)^2} \cdot 1} \\[0.8em] &= \frac{1}{\sqrt{1+2k+k^2 + 1 -2k +k^2 + 1}}\\[0.8em] &= \frac{1}{\sqrt{2k^2+3}}\end{align*}
Für \(2k^2 = 1\) gilt:
\[\begin{align*}\textcolor{#cc071e}{\sin{\varphi}} = \frac{1}{\sqrt{1+3}} &= \textcolor{#cc071e}{\frac{1}{2}}\\[1.6em] \textcolor{#cc071e}{\varphi} &= \textcolor{#cc071e}{30^{\circ}}\end{align*}\]
Für \(2k^2 > 1\) folgt:
\[\begin{align*}\textcolor{#0087c1}{\sin{\varphi}} &= \frac{1}{\sqrt{2k^2+3}} \textcolor{#0087c1}{< \frac{1}{2}} \\[1.6em]\Rightarrow \; \textcolor{#0087c1}{\varphi} \;&\textcolor{#0087c1}{< 30^{\circ}}\end{align*}\]
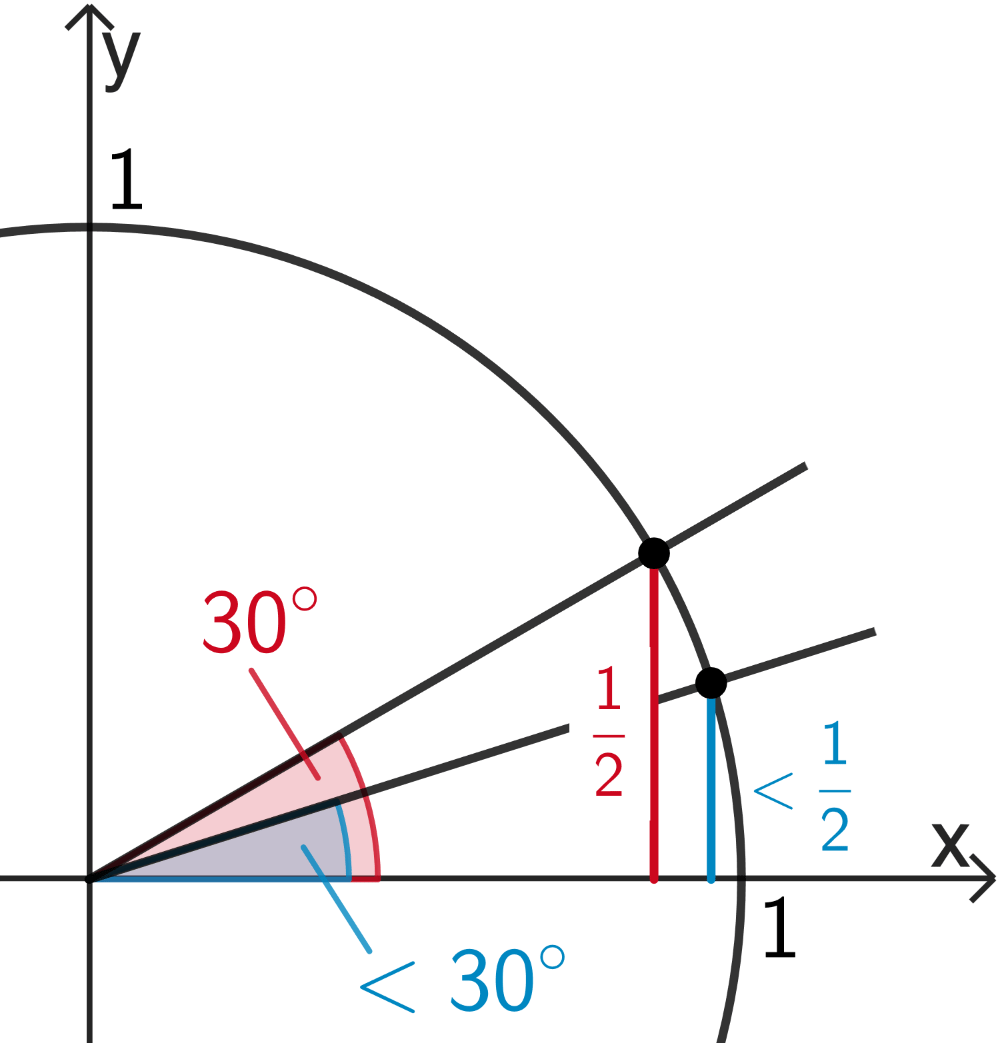Veranschaulichung am Einheitskreis
