Skizzieren Sie im Bereich \(-1 \leq x \leq 4\) den Graphen einer in \(\mathbb R\) definierten Funktion \(f\) mit den folgenden Eigenschaften:
● \(f\) ist nur an der Stelle \(x = 3\) nicht differenzierbar.
● \(f(0)\) = 2 und für die Ableitung \(f'\) von \(f\) gilt: \(f'(0) = -1\).
● Der Graph von \(f\) ist im Bereich \(-1 < x < 3\) linksgekrümmt.
(3 BE)
Lösung zu Teilaufgabe 3
Skizzieren eines Funktionsgraphen nach vorgegebenen Eigenschaften
Bedeutung der vorgegebenen Eigenschaften
\(f\) ist nur an der Stelle \(x = 3\) nicht differenzierbar.
Differenzierbarkeit
Existiert für eine Funktion \(f\) an der Stelle \(x_0\) der Differentialquotient
\(\displaystyle f'(x_0) \, = \, \lim \limits_{x\,\to\,x_0} \frac{f(x) - f(x_0)}{x - x_0} \, = \, \lim \limits_{h\,\to\,0} \frac{f(x_0 + h) - f(x_0)}{h}\,\),
heißt die Funktion \(f\) differenzierbar an der Stelle \(\bf{x_0}\).
Der Differentialquotient existiert, wenn der linksseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#cc071e}{x\,<\,x_0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#cc071e}{h\,<\,0}}{h\,\to\,0}\)) und der rechtsseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#0087c1}{x\,>\,0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#0087c1}{h\,>\,0}}{h\,\to\,0}\)) übereinstimmen.
Der zu skizzierende Funktionsgraph muss an der Stelle \(x = 3\) einen „Knick" oder einen „Sprung" zeigen. In den Intervallen \([-1;3[\) und \(]3;4]\) soll der Graph einen homogenen Verlauf ohne „Knick" oder „Sprung" haben.
Damit ist gewährleistet, dass der Differentialquotient \(\lim \limits_{x \, \to \, 3} \dfrac{f(x) - f(3)}{x - 3}\) nicht existiert, da im Falle eines „Knicks" die Grenzwerte für \(x \to 3^{-}\) und \(x \to 3^{+}\) nicht übereinstimmen bzw. im Falle eines „Sprungs" (einer Unstetigkeit) einer der Grenzwerte nicht vorhanden ist.
Existiert der Differentialquotient \(\lim \limits_{x \, \to \, 3} \dfrac{f(x) - f(3)}{x - 3}\) an der Stelle \(x = 3\) nicht, ist die Funktion \(f\) folglich an der Stelle \(x = 3\) nicht differenzierbar.
\(f(0)\) = 2 und für die Ableitung \(f'\) von \(f\) gilt: \(f'(0) = -1\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Der zu skizzierende Funktionsgraph muss durch den Punkt \((0|2)\) verlaufen. Der Wert der Steigung der Tangente an den Graphen an der Stelle \(x = 0\) soll -1 sein.
Der Graph von \(f\) ist im Bereich \(-1 < x < 3\) linksgekrümmt.
Bewegt man sich im Intervall \(]-1;3[\) auf dem zu skizzierenden Funktionsgraphen in Richtung der positiven \(x\)-Achse, so beschreibt dieser eine Linkskurve.
Es gibt insgesamt beliebig viele Möglichkeiten, den Graphen einer in \(\mathbb R\) definierten Funktion \(f\) mit den genannten Eigenschaften zu skizzieren.
Mögliche Vorgehensweise
Man trägt zunächst den Punkt \((0|2)\) in das Koordinatensystem ein. Mithilfe eines Steigungsdreiecks folgt eine Gerade durch den Punkt \((0|2)\) mit der Steigung \(m = -1\).
Im Intervall \([-1;3[\) zeichnet man nun den ausschließlich linksgekrümmten Teil des Graphen so ein, dass die zuvor skizzierte Gerade an der Stelle \(x = 0\) eine Tangente an den Graphen ist. Hierfür dient beispielweise der Teil einer nach oben geöffneten Parabel.
Abschließend führt man den Graphen im Intervall \(]3;4]\) so fort, dass sich an der Stelle \(x = 3\) ein deutlich sichtbarer „Knick" oder „Sprung" zeigt. Im einfachsten Fall skizziert man eine Gerade.
Der auf diese Weise skizzierte Graph einer Funktion \(f\) ist wie in der Angabe gefordert in \(\mathbb R\) definiert und erfüllt alle genannten Eigenschaften.
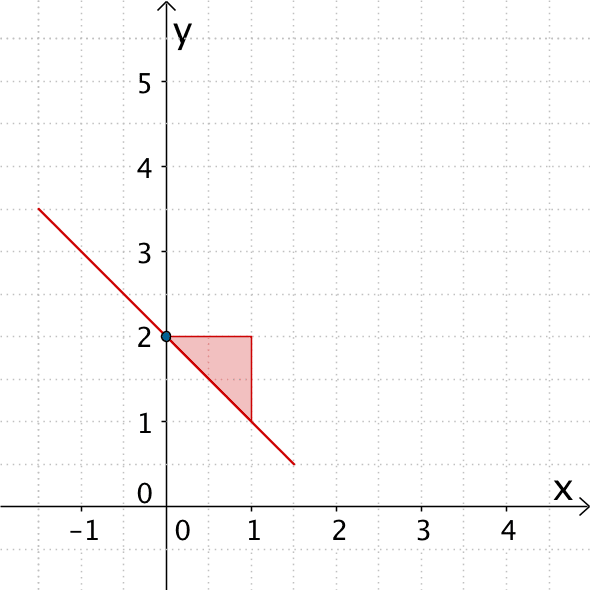
Gerade mit der Steigung -1 durch den Punkt \((0|2)\)
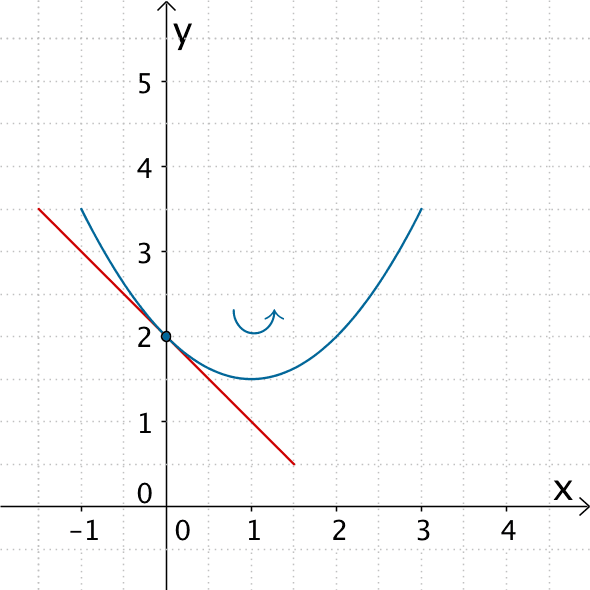
Linksgekrümmter Graph für \(-1 < x < 3\) und der Steigung -1 an der Stelle \(x = 0\)
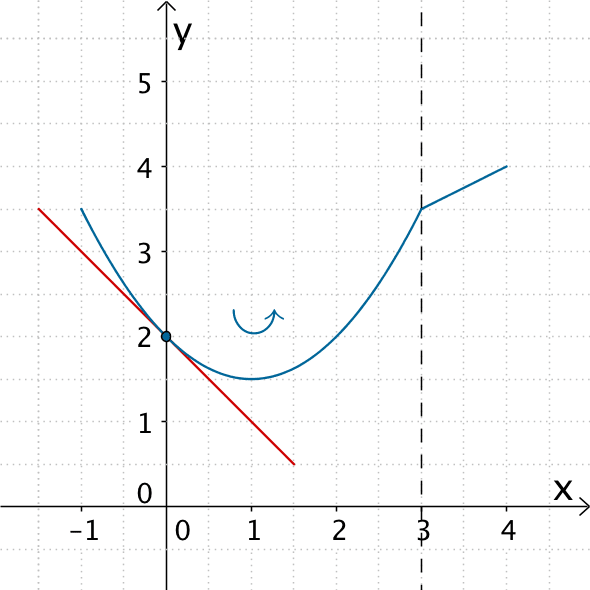
Graph einer in \(\mathbb R\) definierten Funktion \(f\), welche an der Stelle \(x = 3\) nicht differenzierbar ist („Knick").
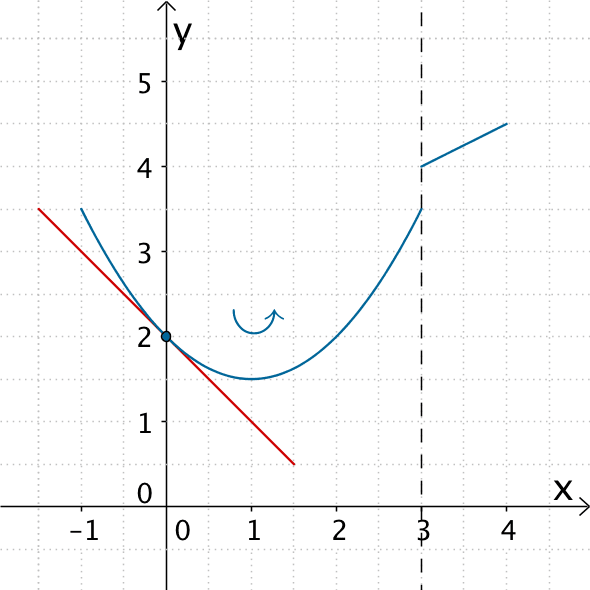
Graph einer in \(\mathbb R\) definierten Funktion \(f\), welche an der Stelle \(x = 3\) nicht differenzierbar (weil nicht stetig) ist („Sprung").

