Gegeben ist die in \(\mathbb R^+\) definierte Funktion \(\displaystyle d\,\colon x \mapsto \frac{1}{\sqrt{x}}\). Bestimmen Sie den Term derjenigen Stammfunktion von \(d\), deren Graph durch den Punkt \((4|-1)\) verläuft.
(3 BE)
Lösung zu Teilaufgabe 4
\[d(x) = \frac{1}{\sqrt{x}}\,; \quad D = \mathbb R^+\]
\[P\,(4|-1)\]
Stammfunktionen von \(d\) bestimmen:
\[d(x) = \frac{1}{\sqrt{x}} = x^{-\frac{1}{2}}\]
Stammfunktion einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad F(x) = \frac{1}{r + 1} \cdot x^{r + 1} + C\]
\[r \neq -1\]
\[\begin{align*} D(x) &= \frac{1}{-\frac{1}{2} + 1} \cdot x^{-\frac{1}{2} + 1} + C \\[0.8em] &= 2 \cdot x^{\frac{1}{2}} + C \\[0.8em] &= 2\sqrt{x} + C \end{align*}\]
Die Menge aller Stammfunktionen der Funktion \(d\) ist gegeben durch das unbestimmte Integral \(\displaystyle \int d(x)\,dx\).
\[\Longrightarrow \quad \int d(x)\,dx = 2\sqrt{x} + C\]
Wert der Integrationskonstante \(C\) bestimmen:
Die Bedingung, dass der Graph einer Stammfunktion von \(d\) durch den Punkt \(P\,(4|-1)\) verlaufen soll, legt den Wert der Integrationskonstanten \(C\) fest.
\[D(x) = 2\sqrt{x} + C\]
\[\begin{align*} P \in D\,\colon\; -1 &= 2\sqrt{4} + C \\[0.8em] -1 &= 4 + C & &| -4 \\[0.8em] -5 &= C \end{align*}\]
\[\Longrightarrow \quad D_{-5}(x) = 2\sqrt{x} - 5\,; \quad D = \mathbb R^+\]
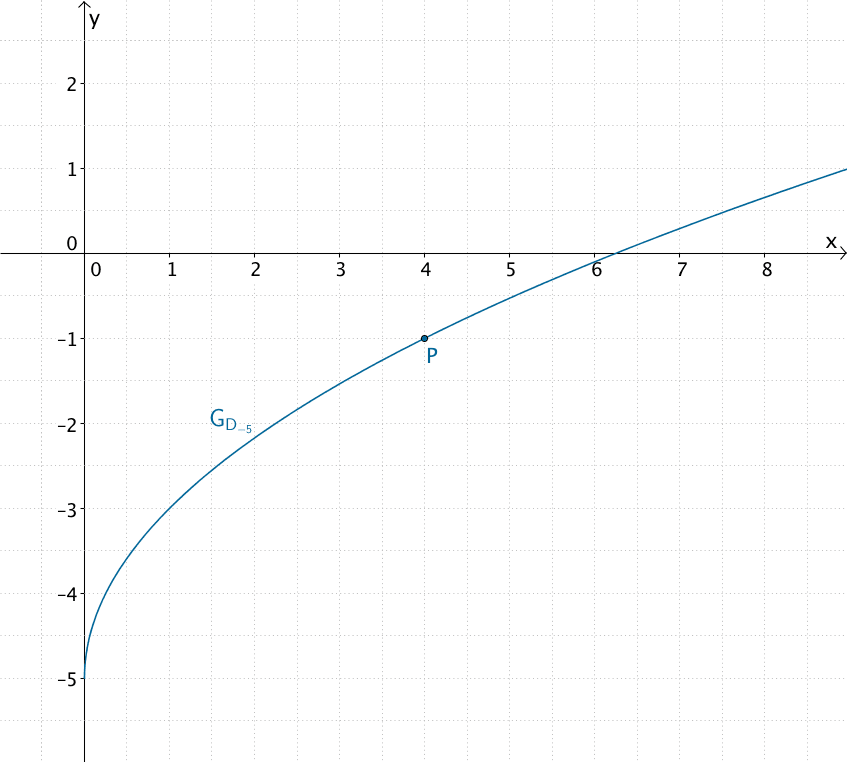
Graph der Stammfunktion \(D_{-5}\), welcher durch den Punkt \(P(4|-1)\) verläuft.

