Bestimmen Sie rechnerisch die Koordinaten desjenigen Graphenpunkts \(Q_E(x_E|y_E)\), der von \(P\) den kleinsten Abstand hat. Tragen Sie \(Q_E\) in Abbildung 1 ein.
(zur Kontrolle: \(x_E = 1\))
(7 BE)
Lösung zu Teilaufgabe 1c
Notwendige Bedingung für eine Exstremstelle:
\(d'(x) \overset{!}{=} 0\)
Erste Ableitung \(d'(x)\) bilden:
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Ableitung einer Wurzelfunktion
\[f(x) = \sqrt{g(x)} \quad \Longrightarrow \quad f'(x) = \frac{g'(x)}{2\sqrt{g(x)}} \quad (g(x) \geq 0)\]
(vgl. Merkhilfe)
\[d(x) = \sqrt{x^2 - 2x + 5{,}25} = \left ( x^2 - 2x + 5{,}25 \right )^{\frac{1}{2}}\]
\[\begin{align*} d'(x) &= \frac{1}{2} \cdot \left ( x^2 - 2x + 5{,}25 \right )^{-\frac{1}{2}} \cdot (2x - 2) \\[0.8em] &= \frac{2x - 2}{2 \sqrt{x^2 - 2x + 5{,}25}} \\[0.8em] &= \frac{x - 1}{\sqrt{x^2 - 2x + 5{,}25}} \end{align*}\]
oder
\[\begin{align*} d'(x) &= \frac{1}{2\sqrt{x^{2} - 2x + 5{,}25}} \cdot (2x - 2) \\[0.8em] &= \frac{2x - 2}{2\sqrt{x^{2} - 2x + 5{,}25}} \\[0.8em] &= \frac{x - 1}{\sqrt{x^{2} - 2x + 5{,}25}} \end{align*}\]
\[\begin {align*} d'(x) = 0 \quad \Longrightarrow \quad x - 1 &= 0 \\ x &= 1 \end {align*}\]
Nachweis, dass \(d\) an der Stelle \(x = 1\) ein Minimum hat:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[d'(x) = \frac{x - 1}{\underbrace{\sqrt{x^2 - 2x + 5{,}25}}_{>~0}}\]
\(x < 1 \quad \Longrightarrow \quad d'(x) < 0 \quad \Longrightarrow \quad d(x)\) fällt im Intervall \(]-\infty;1]\) streng monoton.
\(x > 1 \quad \Longrightarrow \quad d'(x) > 0 \quad \Longrightarrow \quad d(x)\) steigt im Intervall \([1;+\infty[\) streng monoton.
\(\Longrightarrow \quad d(x)\) hat an der Stelle \(x_E = 1\) ein Minimum.
\[\Longrightarrow \quad x_E = 1, \quad f(x_E) = \sqrt{1 + 3} = 2 \quad \Longrightarrow \quad Q_E(1|2)\]
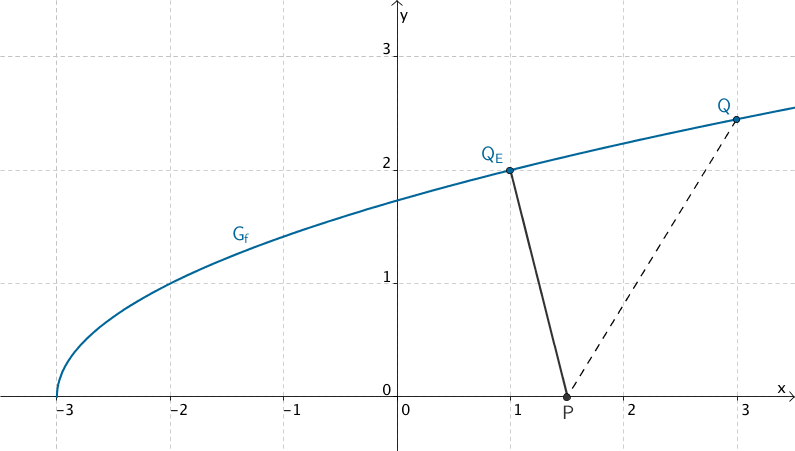
Der Graphenpunkt \(Q_E(1|2)\) hat vom Punkt \(P(1{,}5|0)\) den kleinsten Abstand.


