Für jeden positiven Wert von \(a\) bilden der Hochpunkt \((v|f_a(v))\) des Graphen von \(f_a\), der Punkt \(\left(0|\frac{2}{v}\right)\), der Koordinatenursprung und der Punkt \((v|0)\) die Eckpunkt eines Vierecks. Bestimmen Sie ausgehend von einer geeigneten Skizze denjenigen Wert von \(a\), für den das Viereck den Flächeninhalt 49 hat.
(6 BE)
Lösung zu Teilaufgabe 2g
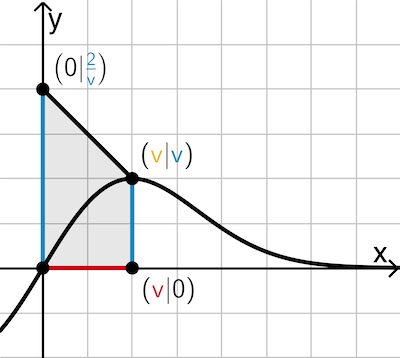
Der Hochpunkt hat die Koordinaten \((v|v)\), da er auf der Gerade mit der Gleichung \(y = x\) liegt (vgl. Teilaufgabe 2f).
Die Punkte \((0|0)\), \((\textcolor{#cc071e}{v}|0)\), \((\textcolor{#e9b509}{v}|\textcolor{#0087c1}{v})\) und \(\left(0|\textstyle \textcolor{#0087c1}{\frac{2}{v}}\right)\) bilden ein Trapez mit den Längen \(\textcolor{#0087c1}{v}\) und \(\textcolor{#0087c1}{\frac{2}{v}}\) der zueinander parallel liegenden Seiten sowie der Höhe \(\textcolor{#cc071e}{v}\).
Der Flächeninhalt des Trapezes soll 49 sein. Mit dieser Bedingung lässt sich zunächst eine Beziehung für die \(\textcolor{#e9b509}{x}\)-Koordinate \(\textcolor{#e9b509}{v}\) der Hochpunkte formulieren.
Flächeninhalt eines Trapezes
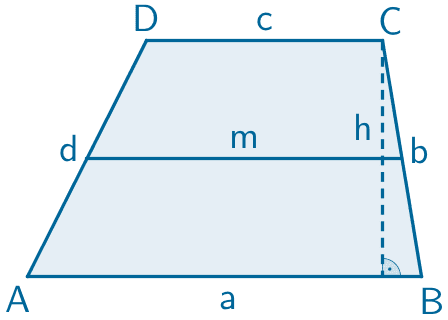
\[A = m \cdot h = \frac{a + c}{2} \cdot h\]
\[\begin{align*} A_{\text{Trapez}} &= 49 \\[0.8em] \frac{\textcolor{#0087c1}{v} + \textcolor{#0087c1}{\frac{2}{v}}}{2} \cdot \textcolor{#cc071e}{v} &= 49 \\[0.8em] \frac{v^2 + 2}{2} &= 49 &&| \cdot 2 \\[0.8em] v^2 + 2 &= 98 &&| -2 \\[0.8em] \textcolor{#e9b509}{v^2} &= 96 \end{align*}\]
Die Gleichung \(a\textcolor{#e9b509}{x^2} = 1\) aus Teilaufgabe 2e beschreibt eine Beziehung zwischen der \(\textcolor{#e9b509}{x}\)-Koordinate der Hochpunkte der Graphen von \(f_a\) und dem Parameter \(a\).
Damit ergibt sich:
\[\begin{align*} a\textcolor{#e9b509}{v^2} &= 1 \\[0.8em] a \cdot 96 &= 1 &&| : 96 \\[0.8em] a &= \frac{1}{96} \end{align*}\]


