Im Modell gibt es einen Zeitpunkt \(x_M\), zu dem die Blumen am schnellsten wachsen. Bestimmen Sie mithilfe von Abbildung 2 einen Näherungswert für \(x_M\). Ermitteln Sie anschließend einen Näherungswert für die maximale Wachstumsrate in Zentimetern pro Tag.
(5 BE)
Lösung zu Teilaufgabe 2c
Der Zeitpunkt \(x_M\,\), zu dem die Sonnenblumen am schnellsten wachsen, entspricht der Wendestelle von \(G_f\). Die Steigung der Tangente an \(G_f\) im Wendepunkt \(W\) (maximale lokale Änderungsrate) beschreibt die maximale Wachstumsrate.
1. Graphische Lösung
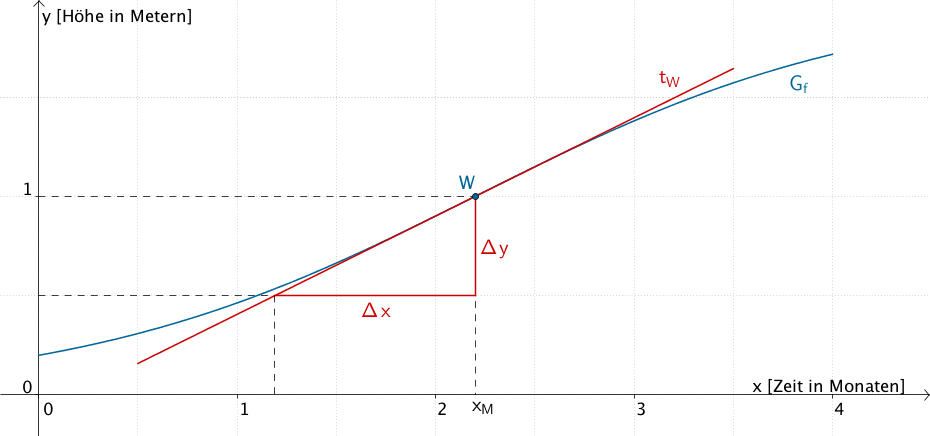
Im Rahmen der Zeichengenauigkeit abzulesen:
\[x_M \approx 2{,}2 \pm 0{,}2 \,\text{Monate}\]
\[f'(x_M) = \frac{\Delta \, y}{\Delta \, x} \approx 0{,}5 \pm 0{,}1 \frac{\text{m}}{\text{Monat}}\]
Maximale Wachstumsrate in Zentimeter pro Tag:
1 Monat entspricht 28 - 31 Tage.
\[f'(x_M) = 0{,}5 \, \frac{\text{m}}{\text{Monat}} = \frac{100\; \text{cm}}{30\, \text{Tage}} \approx 1{,}7\, \frac{\text{cm}}{\text{d}}\]
2. Rechnerische Lösung
Es genügt, den grafisch ermittelten Näherungswert für \(x_M\) in die Ableitung \(f'(x)\) aus Teilaufgabe 1c einzusetzen.
\[f'(x) = \frac{18e^x}{(e^x + 9)^2}\]
\[f'(2{,}2) = \frac{18 \cdot e^{2{,}2}}{(e^{2{,}2} + 9)^2} \approx 0{,}5\]
\[0{,}5 \, \frac{\text{m}}{\text{Monat}} = \frac{100\; \text{cm}}{30\, \text{Tage}} \approx 1{,}7\, \frac{\text{cm}}{\text{d}}\]
Ergänzung: vollständig rechnerische Lösung
Wendepunkt \(W\) von \(G_f\)
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
Zweite Ableitung \(f''(x)\) bilden:
\(\displaystyle f'(x) = \frac{18e^x}{(e^x + 9)^2}\;\) (siehe Teilaufgabe 1c)
Quotientenregel
\[ f(x) = \frac{u(x)}{v(x)} \quad \Longrightarrow \quad f'(x) = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{[v(x)]^2}\]
Kettenregel
\[ f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung einer Potenzfunktion
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
(vgl. Merkhilfe)
\[\begin{align*}f''(x) &= \frac{18e^x \cdot (e^x + 9)^2 - 18e^x \cdot 2 \cdot (e^x + 9) \cdot e^x}{(e^x + 9)^4} \\[0.8em] &= \frac{18e^x(e^x + 9) \cdot (e^x + 9 -2e^x)}{(e^x + 9)^4} \\[0.8em] &= \frac{\overbrace{18e^x(e^x + 9)}^{>\,0} \cdot (9 - e^x)}{\underbrace{(e^x + 9)^4}_{>\,0}} \end{align*}\]
\[\begin{align*}f''(x) \overset{!}{=} 0 \quad \Longrightarrow \quad 9 - e^x &= 0 \\[0.8em] e^x &= 9 & &| \; \ln(\dots) \\[0.8em] x &= \ln(9) \\[0.8em] x &= 2\ln(3) \\[0.8em] x &\approx 2{,}2 \end{align*}\]
\[f(\ln(9)) = \frac{2e^{\ln(9)}}{e^{\ln(9)} + 9} = \frac{18}{18} = 1\]
\[\left. \begin{align*} x &< \ln(9) \quad \Longrightarrow \quad 9 - e^x > 0 \quad \Longrightarrow \quad f''(x) > 0 \\[0.8em] x &> \ln(9) \quad \Longrightarrow \quad 9 - e^x < 0 \quad \Longrightarrow \quad f''(x) < 0 \end{align*} \right \} \Longrightarrow W\,(2\ln(3)|1)\]
\[\Longrightarrow \quad x_M = 2\ln(3) \approx 2{,}2\]
Maximale Wachstumsrate
\[f'(\ln(9)) = \frac{18e^{\ln(9)}}{(e^{\ln(9)} + 9)^2} = \frac{18 \cdot 9}{18^2} = \frac{9}{18} = 0{,}5\]
\[0{,}5 \, \frac{\text{m}}{\text{Monat}} = \frac{100\; \text{cm}}{30\, \text{Tage}} \approx 1{,}7\, \frac{\text{cm}}{\text{d}}\]

