Betrachtet wird die Schar der in \(\mathbb R\) definierten Funktionen \(g_k \colon x \mapsto -5x \cdot e^{-kx}\) mit \(k \in \mathbb R \backslash \{0\}\). Abbildung 3 zeigt vier Graphen der Schar, die zu den Werten \(k = -1\), \(k = -0{,}5\), \(k = 0{,}5\) und \(k = 1\) gehören.
Der Graph III kann durch Spiegeln von \(G\) (vgl. Abbildung 1) an der \(x\)-Achse erzeugt werden. Geben Sie den zugehörigen Wert von \(k\) sowie die Koordinaten des Tiefpunkts von Graph III an. Ordnen Sie den drei übrigen Werten von \(k\) den jeweils passenden Graphen zu.
 Abb. 3
Abb. 3
(5 BE)
Lösung zu Teilaufgabe 2a
\[g_k(x) = -5x \cdot e^{-kx}; \; D_{g_k} = \mathbb R, \; k \in \mathbb R \backslash \{0\}\]
Wert von \(k\) und Koordinaten des Tiefpunkts von Graph III
\(k = 1\)
Koordinaten des Tiefpunkts: \(\big(1|-\frac{5}{e}\big)\)
Begründung (nicht verlangt)
\(G\) ist der Graph der Funktion \(f\) mit \(f(x) = 5x \cdot e^{-x}\) (vgl. Aufgabe 1)
Spiegelung an der \(x\)-Achse:
Wie verändern die Parameter \(a\), \(b\), \(c\) und \(d\) den Graphen einer Funktion \(x \mapsto a \cdot f(b \cdot (x + c)) + d\) gegenüber dem Graphen einer Funktion \(x \mapsto f(x)\)?
Erst strecken oder spiegeln, dann verschieben!
Ein Vertauschen der Reihenfolge von Strecken und Verschieben bzw. Spiegel und Verschieben ergibt unterschiedliche Graphen und Funktionsterme.


Strecken in \(\boldsymbol{y}\)-Richtung mit dem Faktor \(\textcolor{#e9b509}{\boldsymbol{a}}\)
\(g(x) = \textcolor{#e9b509}{a} \cdot f(x)\) mit \(a \in \mathbb R\)
\(a < 0\) bewirkt zusätzlich eine Spiegelung an der \(x\)-Achse.

Strecken in \(\boldsymbol{x}\)-Richtung mit dem Faktor \(\textcolor{#e9b509}{\boldsymbol{\dfrac{1}{b}}}\)
\(h(x) = f(\textcolor{#e9b509}{b} \cdot x)\) mit \(b \in \mathbb R\)
\(b < 0\) bewirkt zusätzlich eine Spiegelung an der \(y\)-Achse.

Verschieben in \(\boldsymbol{y}\)-Richtung um \(\textcolor{#e9b509}{\boldsymbol{d}}\)
\(k(x) = f(x) + \textcolor{#e9b509}{d}\) mit \(d \in \mathbb R\)

Verschieben in \(\boldsymbol{x}\)-Richtung um \(\textcolor{#e9b509}{\boldsymbol{-c}}\)
\(l(x) = f(x + \textcolor{#e9b509}{c})\) mit \(c \in \mathbb R\)
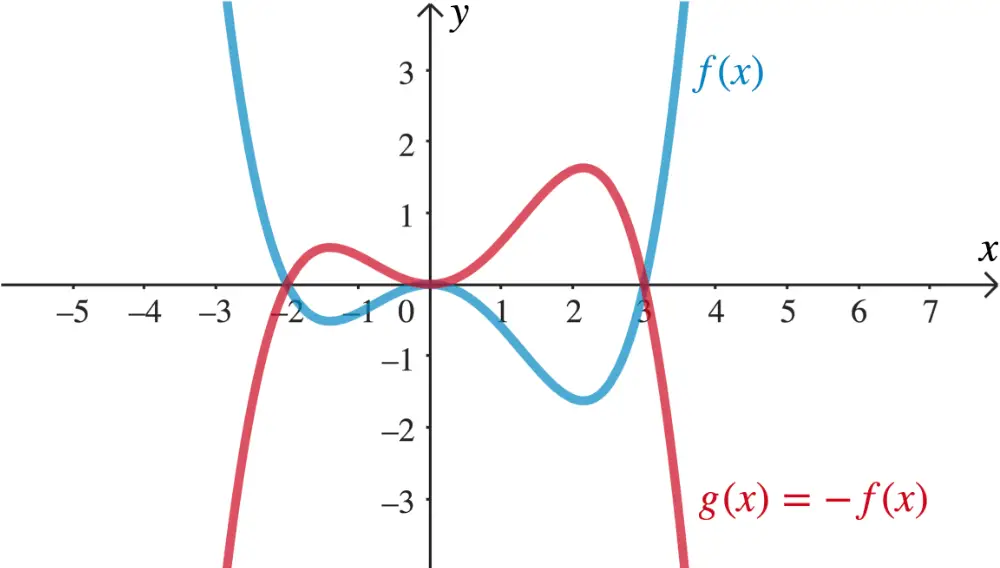
Spiegelung an der \(\boldsymbol{x}\)-Achse
\[g(x) = -f(x)\]

Spiegelung an der \(\boldsymbol{y}\)-Achse
\[h(x) = f(-x)\]
\(-f(x) = -5x \cdot e^{-x} = g_1(x)\) für \(k = 1\)
Graph \(G\) besitzt den Hochpunkt \(\big(1|\textcolor{#cc071e}{\frac{5}{e}}\big)\) (vgl. Teilaufgabe 1a, Abbildung 1). Da Graph III durch Spiegeln von \(G\) an der \(\textcolor{#cc071e}{x}\)-Achse erzeugt werden kann (vgl. Angabe), besitzt Graph III den Tiefpunkt \(\big( 1|\textcolor{#cc071e}{-\frac{5}{e}}\big)\).
Zuordnung der Graphen I, II und IV zu den übrigen Werten von \(k\)
\(k = 0{,}5\) gehört zu Graph IV.
\(k = -0{,}5\) gehört zu Graph I.
\(k = -1\) gehört zu Graph II.
Mögliche Überlegungen für die Zuordnung (nicht verlangt)

Da \(k = 0{,}5\) ein positiver Wert ist, sollte der zugehörige Graph einen ähnlichen charakteristischen Verlauf haben wie Graph III für den positiven Wert \(k = 1\). Dafür kommt nur Graph IV in Frage.
Die Graphen I und IV sowie II und III sind punktsymmetrisch bezüglich des Koordinatenursprungs. Dieses Symmetrieverhalten kann nur für betragsmäßig gleiche Werte von \(k\) gelten (vgl. Teilaufgabe 2b).
Somit gehört \(k = -0{,}5\) zu Graph I und \(k = -1\) zu Graph II.


