Geben Sie den Zusammenhang zwischen der Funktion \(F\) und dem Ergebnis der Aufgabe 1e an.

(1 BE)

Lösung zu Teilaufgabe 1g

\[F(x) = \int_{a}^{x}f(t)\,dt\,; \quad D = \mathbb R\]

Ergebnis aus Teilaufgabe 1e:

\[\int_{0}^{a}f(x)\,dx \approx 1{,}66\]

Mithilfe des Ergebnisses aus Teilaufgabe 1e lässt sich \(F(0)\) näherungsweise berechnen.

\[F(0) = \int_{a}^{0}f(t)\,dt = -\int_{0}^{a} f(t)\,dt \approx -1{,}66\]

Der Graph der Intergrafunktion \(F\) schneidet die \(y\)-Achse näherungsweise im Punkt \((0|-1{,}66)\).

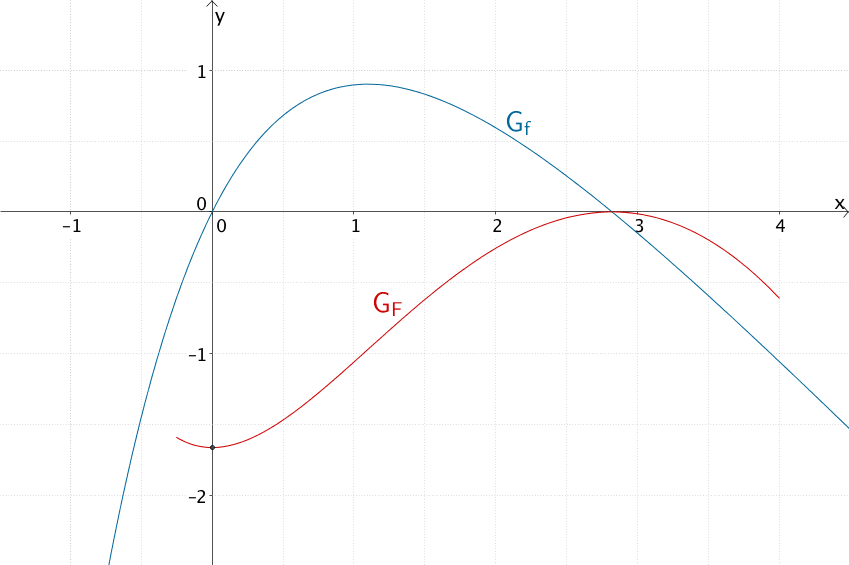
Schnittpunkt des Graphen der Integralfunktion \(F\) mit der \(y\)-Achse