Für die in \(\mathbb R\) definierte erste Ableitungsfunktion \(f'\) von \(f\) gilt \(f'(-x) = f'(x)\). Geben Sie die Bedeutung dieser Tatsache im Hinblick auf den Verlauf des Graphen von \(f'\) an und skizzieren Sie in der Abbildung den Graphen von \(f'\).
(3 BE)
Lösung zu Teilaufgabe 1c
Bedeutung der Beziehung \(f'(-x) = f'(x)\) für den Verlauf des Graphen von \(f'\)
Der Graph von \(f'\) ist bezüglich der \(y\)-Achse symmetrisch.
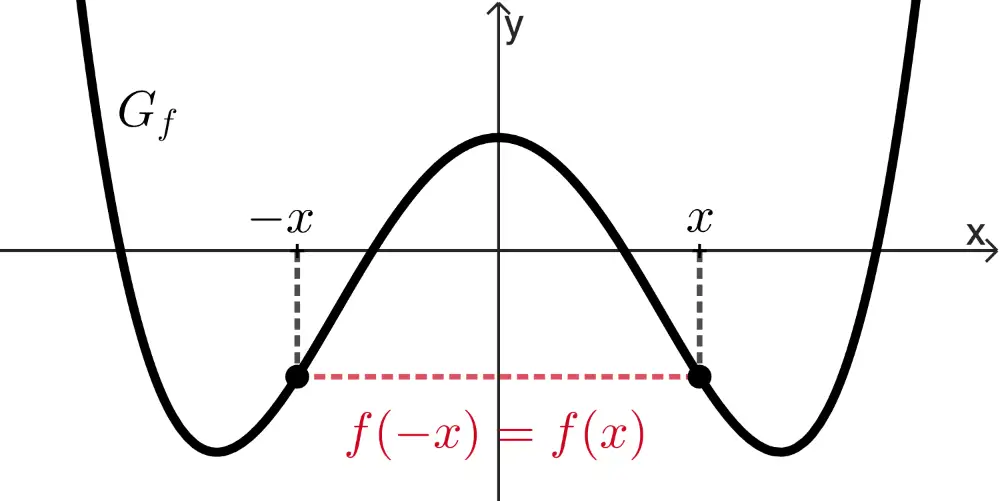
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
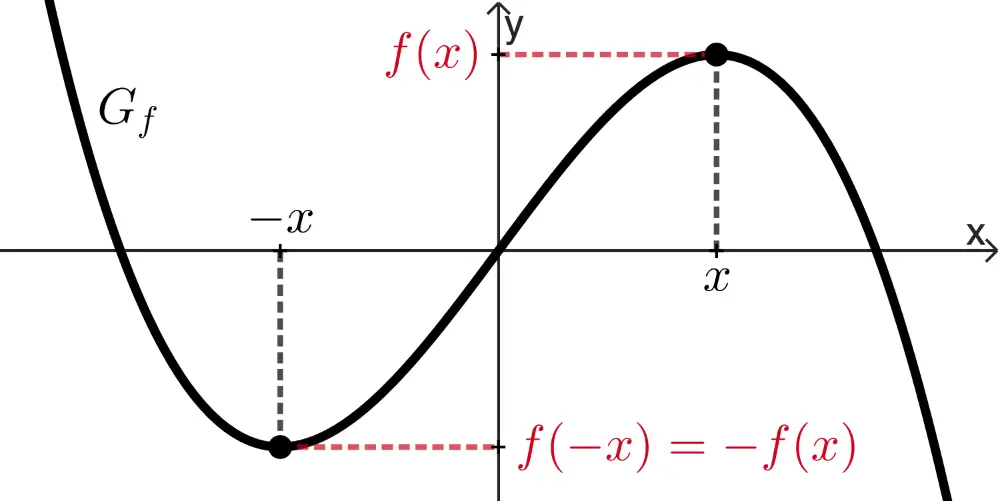
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
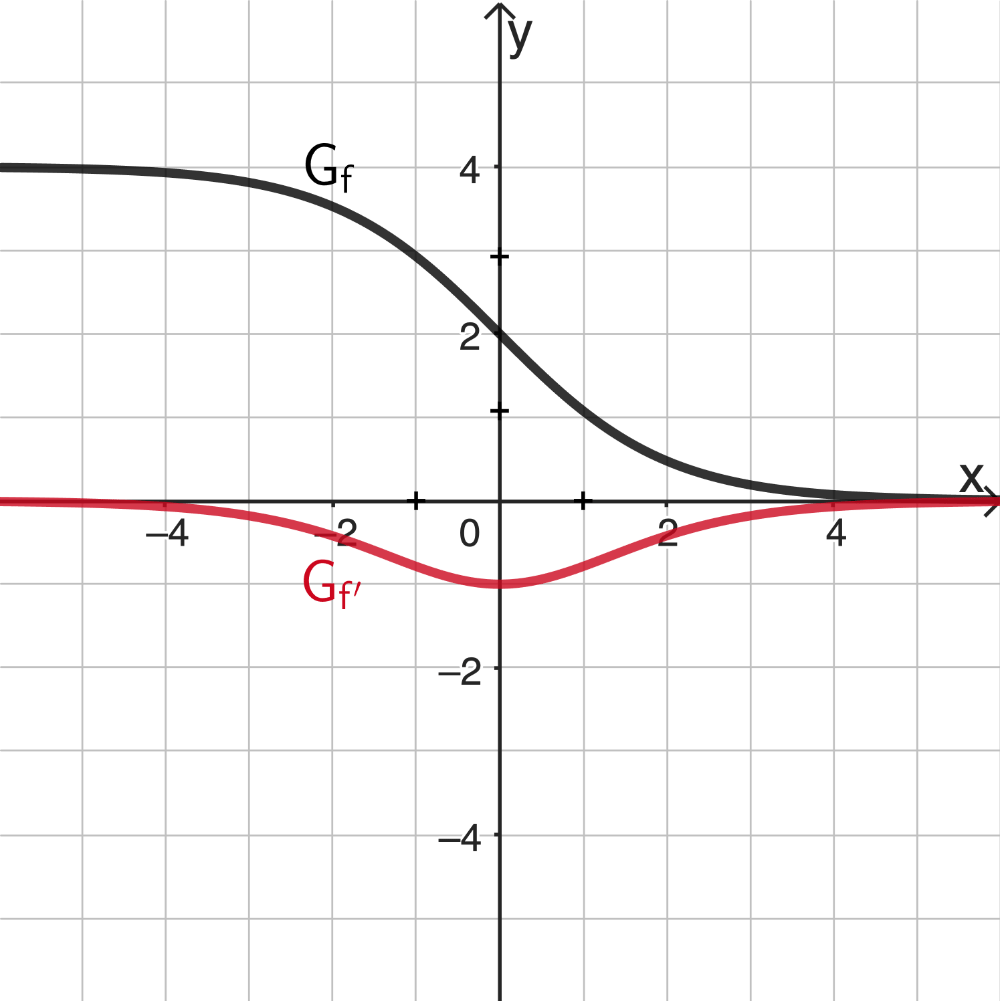
Skizze des Graphen von \(f'\)
Ergänzende Erklärung (nicht verlangt)
Da \(G_f\) in \(\mathbb R\) streng monoton fällt, gilt \(\textcolor{#cc071e}{f'(x) < 0}\) für alle \(x \in \mathbb R\). Somit verläuft der Graph von \(f'\) vollständig unterhalb der \(x\)-Achse.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Betrachtung des Wendepunkts von \(G_f\)
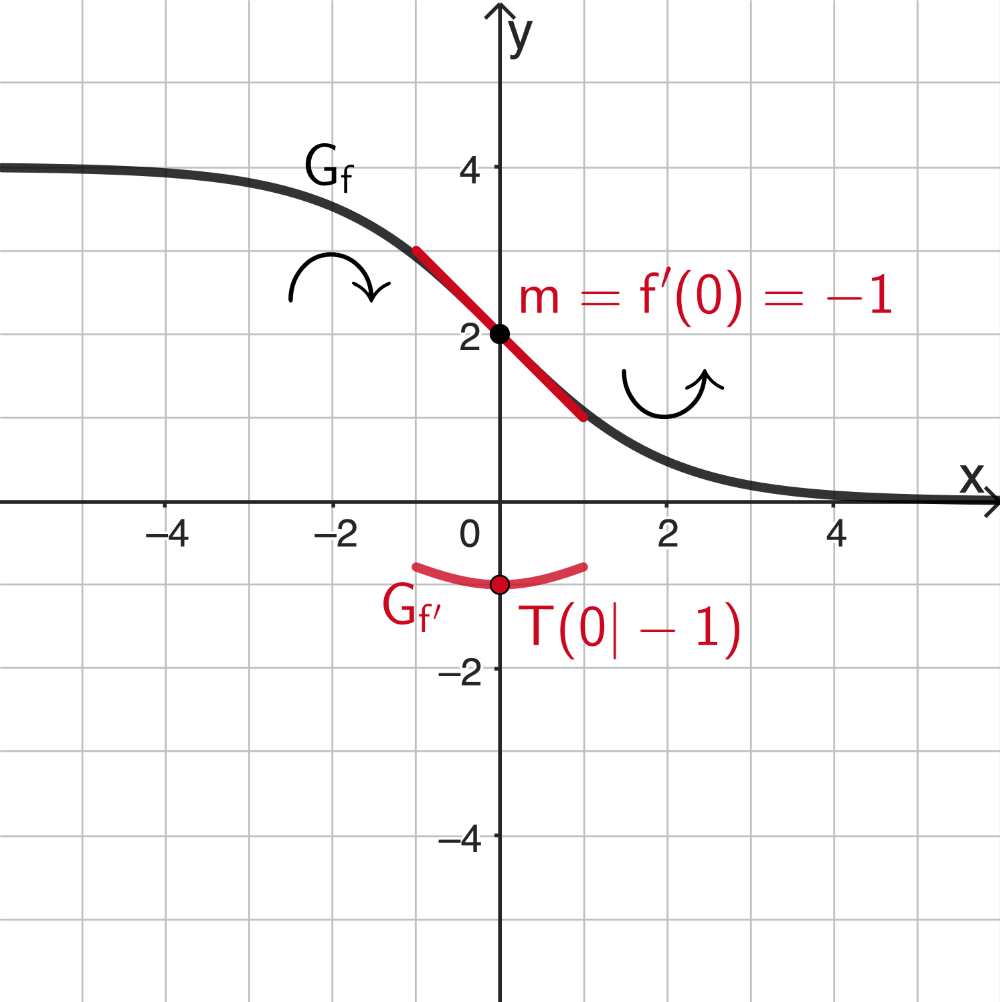
Im Wendepunkt \((0|2)\) wechselt \(G_f\) das Krümmungsverhalten von rechtsgekrümmt \(\curvearrowright\) nach linksgekrümmt \(\style{display: inline-block; transform:rotate(0.5turn);}{ \curvearrowleft}\) und die Steigung von \(G_f\) erreicht mit \(\textcolor{#cc071e}{-1}\) ein absolutes Minimum (vgl. Teilaufgabe 1b). Folglich besitzt der Graph von \(f'\) den absoluten Tiefpunkt \(\textcolor{#cc071e}{T(0|-1)}\).
Betrachtung des Verhaltens von \(G_f\) für \(x \to -\infty\) und \(x \to +\infty\)
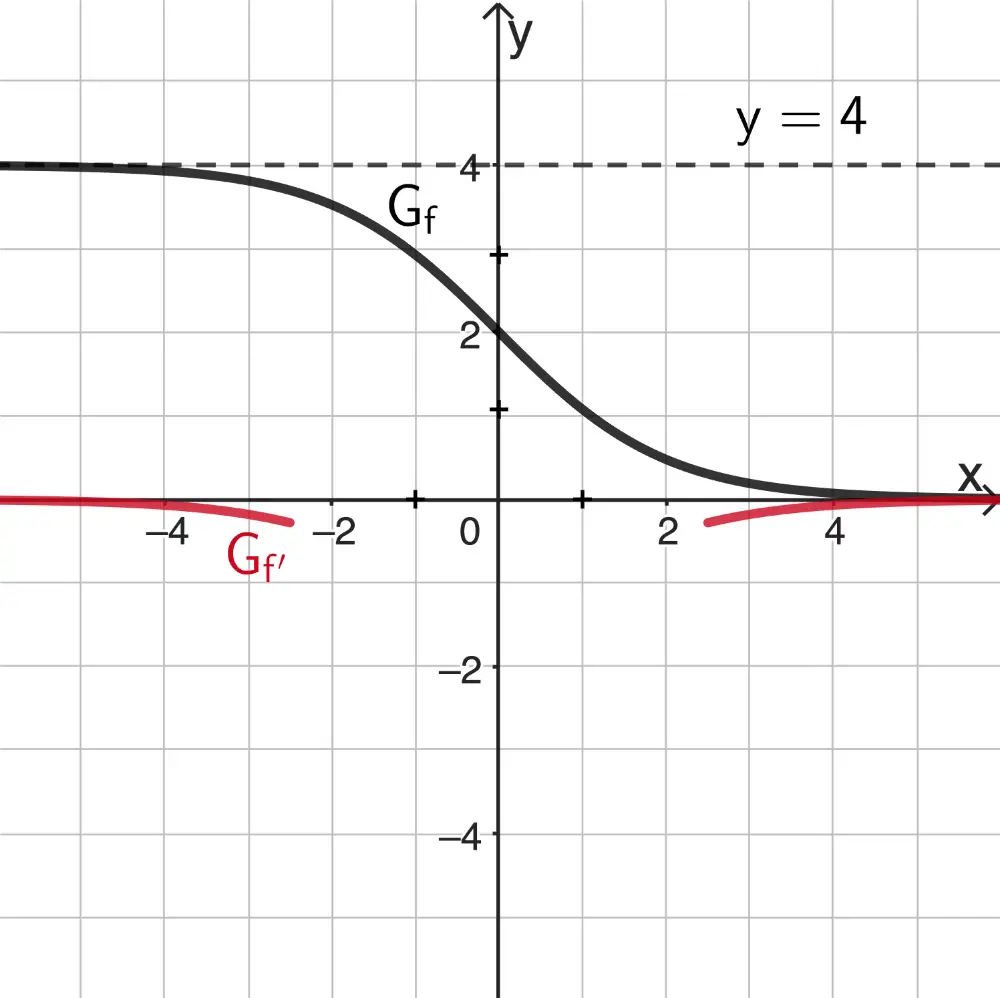
Für \(x \to -\infty\) besitzt \(G_f\) die waagrechte Asymptote mit der Gleichung \(y = 4\) und für \(x \to +\infty\) die waagrechte Asymptote mit der Gleichung \(y =0\) (\(x\)-Achse). Die Ergebnisse \(\lim \limits_{x\,\to\,-\infty}f(x) = 4\) und \(\lim \limits_{x\,\to\,+\infty} f(x) = 0\) aus Teilaufgabe 1a bestätigen dies. Da \(G_f\) zudem in \(\mathbb R\) streng monoton fällt, besitzt \(G_f\) im Unendlichen die Steigung \(\textcolor{#cc071e}{0^-}\) (nahe null, aber negativ). Somit nähert sich der Graph von \(f'\) im Unendlichen asymptotisch von unten der \(\textcolor{#cc071e}{x}\)-Achse an, wobei der Verlauf symmetrisch bezüglich der \(y\)-Achse ist (vgl. oben).


