Zeigen Sie, dass es einen Wert von \(k > 0\) gibt, für den \(A(k)\) maximal ist. Berechnen Sie diesen Wert von \(k\) sowie den Flächeninhalt des zugehörigen Dreiecks \(P_{k}Q_{k}R\).
(6 BE)
Lösung zu Teilaufgabe 3b
\[A(k) \frac{2k}{x^{2} + 1}; \; k > 0\]
Nachweis, dass es einen Wert von \(k > 0\) gibt, für den \(A(k)\) maximal ist sowie Berechnung des Wertes von \(k\)
Es ist nachzuweisen, dass es einen Wert \(k > 0\) gibt, sodass \(A'(k) = 0\) gilt und zudem \(A'\) in der Umgebung dieses Werts von \(k\) das Vorzeichen von \(+\) nach \(-\) wechselt.
Anmerkung:
Die Vorgehensweise ist vergleichbar mit dem Nachweis eines Hochpunkts des Graphen einer gegebenen Funktion.
Erste Ableitung \(A'\) bilden:
Hierfür wird die Quotientenregel, die Summenregel sowie die Ableitung einer Potenzfunktion benötigt.
\[A(k) \frac{\textcolor{#0087c1}{2k}}{\textcolor{#cc071e}{x^{2} + 1}}; \; k > 0\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[\begin{align*}A'(k) &= \frac{\textcolor{#0087c1}{2} \cdot (\textcolor{#cc071e}{k^{2} + 1}) - \textcolor{#0087c1}{2k} \cdot (\textcolor{#cc071e}{2k + 0})}{(\textcolor{#cc071e}{k^{2} + 1})^{2}} \\[0.8em] &= \frac{2k^{2} + 2 -4k^{2}}{(k^{2} + 1)^{2}} \\[0.8em] &= \frac{2 - 2k^{2}}{(k^{2} + 1)^{2}} \\[0.8em] &= \frac{2 \cdot (1 - k^{2})}{(k^{2} + 1)^{2}} \end{align*}\]
Die notwendige Bedingung für einen Wert \(k > 0\), sodass \(A(k)\) maximal ist, lautet: \(A'(k) = 0\).
Ein Quotient ist gleich Null, wenn der Zähler gleich Null ist.
\[\begin{align*}A'(k) = 0 \quad \Longrightarrow \quad 1 - k^{2} &= 0 &&| + k^{2} \\[0.8em] 1 &= k^{2} &&| \; \sqrt{\quad} \enspace (k > 0) \\[0.8em] 1 &= k \end{align*}\]
Prüfen, ob an der Stelle \(k = 1\) ein Maximum von \(A(k)\) vorliegt, beispielsweise mithilfe einer Vorzeichentabelle für \(A'\).
1. Möglichkeit: Vorzeichentabelle von \(A'\)
\[A'(k) = \frac{2 \cdot \textcolor{#cc071e}{(1 - k^{2})}}{\underbrace{(k^{2} + 1)^{2}}_{>\,0}}\]
Da der Wert des Nenners von \(A'\) stets größer Null ist, bestimmt der Faktor \(\textcolor{#cc071e}{(1 - k^{2})}\) des Zählers von \(A'\) den Vorzeichenwechsel von \(A'\) an der Stelle \(k = 1\).
| \(k\) | \(\textcolor{#cc071e}{0 < k < 1}\) | \(1\) | \(\textcolor{#cc071e}{x > 1}\) |
| \(\textcolor{#cc071e}{1 - k^{2}}\) | \(\textcolor{#cc071e}{+}\) | \(0\) | \(\textcolor{#cc071e}{-}\) |
| \(A'(k)\) | \(+\) | \(\text{Maximum}\) | \(-\) |
Oder mithilfe von Testwerten:
\[\textcolor{#cc071e}{A'(0{,}5)} = \frac{2 \cdot \overbrace{(1 - 0{,}5^{2})}^{>\,0}}{\underbrace{(0{,}5^{2} + 1)^{2}}_{>\,0}} \textcolor{#cc071e}{> 0}\]
\[\textcolor{#cc071e}{A'(2)} = \frac{2 \cdot \overbrace{(1 - 2^{2})}^{<\,0}}{\underbrace{(2^{2} + 1)^{2}}_{>\,0}} \textcolor{#cc071e}{< 0}\]
Da \(\textcolor{#cc071e}{A'(1) = 0}\) gilt und zudem \(\textcolor{#cc071e}{A'}\) an der Stelle \(k = 1\) einen Vorzeichenwechsel von \(\textcolor{#cc071e}{+}\) nach \(\textcolor{#cc071e}{-}\) hat, ist \(\textcolor{#cc071e}{A(1)}\) maximal.
2. Möglichkeit: halbgraphischer Nachweis des Vorzeichenwechsels von \(A'\)
\[A'(k) = \frac{2 \cdot \textcolor{#cc071e}{(1 - k^{2})}}{\underbrace{(k^{2} + 1)^{2}}_{>\,0}}\]
Der quadratische Faktor \(\textcolor{#cc071e}{(1 - k^{2})}\) des Zählers bestimmt den Vorzeichenwechsel von \(A'\). Dieser Faktor kann durch die Parabel mit der Gleichung \(\textcolor{#cc071e}{y = -k^{2} + 1}\) veranschaulicht werden. Da \(k > 0\) gilt, genügt eine qualitative Skizze des entsprechenden Parabelasts unter Berücksichtigung der Nullstelle \(k = 1\) (vgl. Nullstelle \(k = 1\) von \(A'\)).
Da die Parabel mit der Gleichung \(\textcolor{#cc071e}{y = -k^{2} + 1}\) an der Nullstelle \(k = 1\) von \(\textcolor{#cc071e}{+}\) nach \(\textcolor{#cc071e}{-}\) verläuft, hat \(\textcolor{#cc071e}{A'}\) einen Vorzeichenwechsel von \(\textcolor{#cc071e}{+}\) nach \(\textcolor{#cc071e}{-}\). Folglich ist \(\textcolor{#cc071e}{A(1)}\) maximal.
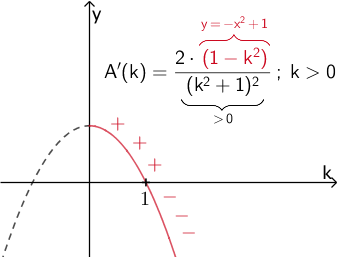
3. Möglichkeit: Nachweis des Maximums mithilfe von \(A''\)
Diese Möglichkeit sei der Vollständigkeit halber aufgeführt. Sie ist zeitaufwendiger und deshalb in diesem Fall nicht zu empfehlen.
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
Zweite Ableitung \(A''\) bilden:
Hierfür wird die Summenregel, die Faktorregel, die Quotientenregel und die Kettenregel sowie die Ableitung einer Potenzfunktion benötigt.
\[A'(k) = \frac{\textcolor{#0087c1}{2 \cdot (1 - k^{2})}}{\textcolor{#cc071e}{(k^{2} + 1)^{2}}}\]
\[\begin{align*}A''(k) &= \frac{\textcolor{#0087c1}{2 \cdot (0 - 2k)} \cdot \textcolor{#cc071e}{(k^{2} + 1)^{2}} - \textcolor{#0087c1}{2 \cdot (1 - k^{2})} \cdot \overbrace{\textcolor{#cc071e}{2\cdot(k^{2} + 1) \cdot 2k}}^{\text{Kettenregel}}}{\left[\textcolor{#cc071e}{(k^{2} + 1)^{2}}\right]^{2}} \\[0.8em] &= \frac{-4k \cdot (k^{2} +1)^{2} - 8k \cdot (1 - k^{2}) \cdot (k^{2} + 1)}{(k^{2} + 1)^{4}} \\[0.8em] &= \frac{\cancel{(k^{2} + 1)} \cdot \left[ (-4k) \cdot (k^{2} + 1) - 8k \cdot (1 - k^{2}) \right]}{(k^{2} + 1)^{\cancel{4}{3}}} \\[0.8em] &= \frac{-4k^{3} - 4k - 8k + 8k^{3}}{(k^{2} + 1)^{3}} \\[0.8em] &= \frac{4k^{3} - 12k}{(k^{2} + 1)^{3}} \\[0.8em] &= \frac{4k \cdot (k^{2} - 3)}{(k^{2} + 1)^{3}} \end{align*}\]
Vorzeichen von \(A''\) an der Stelle \(k = 1\) ermitteln:
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
\[\textcolor{#cc071e}{A''(1)} = \frac{4 \cdot 1 \cdot \overbrace{(1^{2} - 3)}^{<\, 0}}{\underbrace{(1^{2} + 1)^{3}}_{> \,0}} \textcolor{#cc071e}{< 0}\]
\(\Longrightarrow \quad \textcolor{#cc071e}{A(1)}\) ist ein Maximum.
Berechnung des maximalen Flächeninhalts \(A(1)\) des Dreiecks \(P_{1}Q_{1}R\)
\[A(k) \frac{2k}{x^{2} + 1}\]
\[\textcolor{#e9b509}{k = 1}\]
\[A(\textcolor{#e9b509}{1}) = \frac{2 \cdot \textcolor{#e9b509}{1}}{\textcolor{#e9b509}{1}^{2} + 1} = \frac{2}{2} = 1\]


