Kann die Wahrscheinlichkeit dafür, dass eine Zufallsvariable einen Wert annimmt, der kleiner als ihr Erwartungswert ist, größer als 50 % sein? Begründen Sie Ihre Antwort.
(4 BE)
Lösung zu Teilaufgabe 2b
Antwort: Ja.
Begründung durch Beispiel
Vorüberlegung:
Der Erwartungswert \(\mu\) einer binomialverteilten Zufallsgröße \(X\) ist in der Regel keine Trefferanzahl \(k\). Für \(\mu \neq k\,;\; k \in \mathbb N\) sind die Wahrscheinlichkeiten der dem Erwartungswert benachbarten Trefferanzahlen am größten.
Die Binomialverteilung ist für \(p = 0{,}5\) symmetrisch. Für \(0 < p < 0{,}5\) ist das Maximum der Wahrscheinlichkeitsverteilung hin zu kleinen Trefferanzahlen verschoben (nach links). Eine Wahrscheinlichkeit \(P(X < \mu) > 0{,}5\) wird man deshalb für kleine Trefferwahrscheinlichkeiten \(p\) erwarten.
Die Summe der Wahrscheinlichkeiten aller Trefferanzahlen \(k\) ist gleich Eins: \(P^{n}_{p}(X \leq n) = 1\). Je kleiner die Länge \(n\) einer Bernoullikette ist, desto größer sind die Wahrscheinlichkeiten \(P(X = k)\) für die Trefferanzahlen \(k\). Folglich findet man Wahrscheinlichkeiten \(P(X = k) > 0{,}5\) vor allem für Bernoulliketten kleiner Längen \(n\).
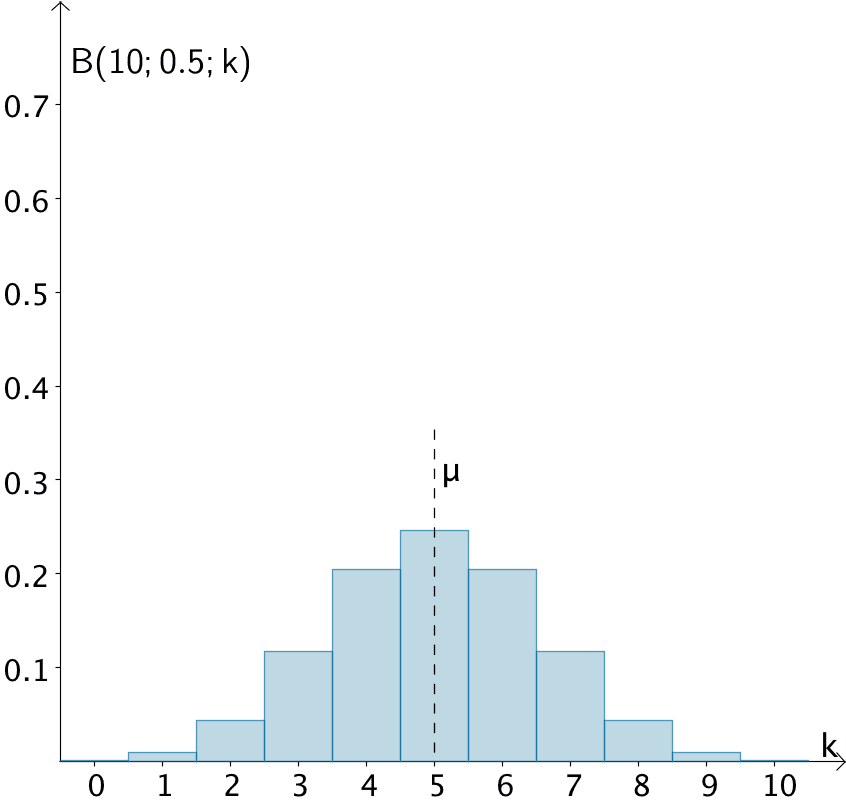
Wahrscheinlichkeitsverteilung und Erwartungswert \(\mu\) einer nach \(B(10;0{,}5)\) binomialverteilten Zufallsgröße \(X\)
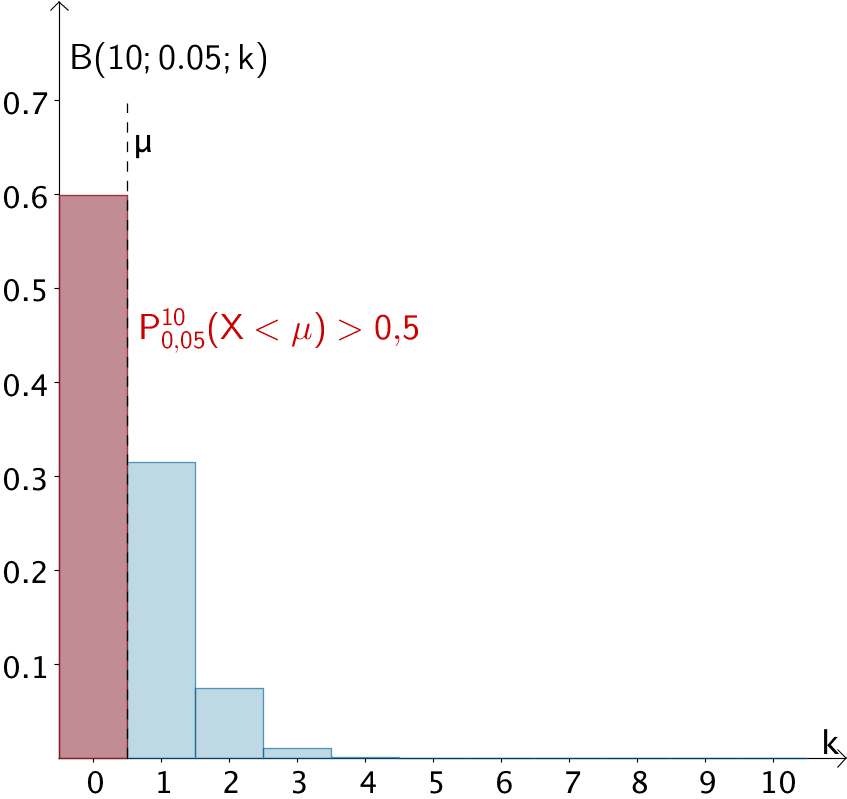
Wahrscheinlichkeitsverteilung und Erwartungswert \(\mu\) einer nach \(B((10;0{,}05)\) binomialverteilten Zufallsgröße \(X\)
Beispiel:
Die Zufallsgröße \(X\) sei nach \(B(10;0{,}05)\) binomialverteilt.
\[n = 10\,; \quad p = 0{,}05\]
Erwartungswert berechnen:
Erwartungswert \(\boldsymbol{\mu}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\(\mu = E(X) = n \cdot p\) (vgl. Merkhilfe)
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist.
\[\mu = E(X) = n \cdot p = 10 \cdot 0{,}05 = 0{,}5\]
\[\Longrightarrow \quad P^{10}_{0{,}05}(X < \mu) = P^{10}_{0{,}05}(X = 0)\]
Stochastisches Tafelwerk (ST) verwenden:
\[P^{10}_{0{,}05} (X = 0) = B(10; 0{,}05, 0) \enspace \overset{ST}{=} \enspace 0{,}59874 \approx 60 \, \%\]
\[\Longrightarrow \quad P^{10}_{0{,}05}(X < \mu) > 0{,}5\]
\(\Longrightarrow \quad\) Die Aussage ist falsch.
Weitere Beispiele:
\[B(3; 0{,}125; k)\]
\[n = 3\,; \quad p = 0{,}125\,; \quad \mu = 0{,}375\,; \qquad P^{3}_{0{,}125}(X = 0) \enspace \overset{ST}{=} \enspace 0{,}66992\]
\[B(5; 0{,}01; k)\]
\[n = 5\,; \quad p = 0{,}01\,; \quad \mu = 0{,}05\,; \qquad P^{5}_{0{,}01}(X = 0) \enspace \overset{ST}{=} \enspace 0{,}95099\]
\[B(8; 0{,}03; k)\]
\[n = 8\,; \quad p = 0{,}03\,; \quad \mu = 0{,}24\,; \qquad P^{8}_{0{,}03}(X = 0) \enspace \overset{ST}{=} \enspace 0{,}78374\]


