Es gibt genau eine Kugel, auf der alle acht Eckpunkte des Körpers liegen. Ermitteln Sie die Koordinaten des Mittelpunkts dieser Kugel.
(4 BE)
Lösung zu Teilaufgabe g
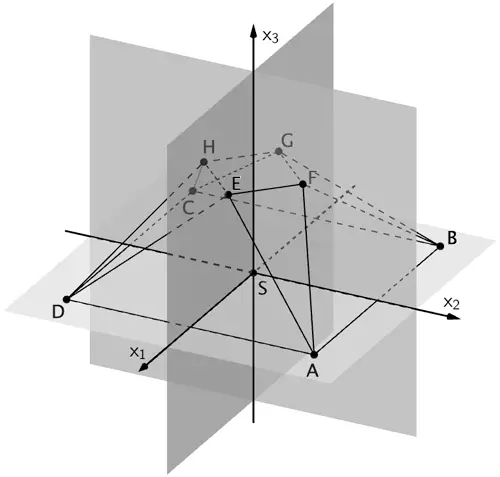
Da der gesamte Körper sowohl symmetrisch bezüglich der \(x_{1}x_{3}\)-Ebene als auch bezüglich der \(x_{2}x_{3}\)-Ebene ist (vgl. Angabe), kann der Mittelpunkt \(M\) einer Kugel, auf der alle acht Eckpunkte des Körpers liegen, nur auf der \(x_{3}\)-Achse liegen.
\[\Rightarrow \enspace M(0|0|m)\]
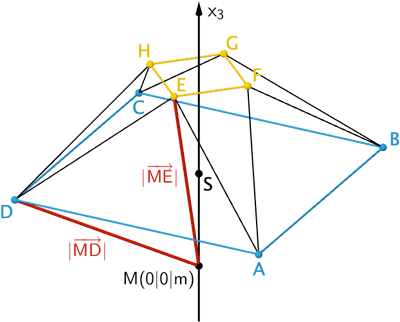
Bedingung: Der Abstand eines Punktes der Grundfläche \(\textcolor{#0087c1}{ABCD}\) vom Mittelpunkt muss gleich dem Abstand eines Punktes des Quadrats \(\textcolor{#e9b509}{EFGH}\) vom Mittelpunkt sein, also beispielsweise \(\textcolor{#cc071e}{\vert\overrightarrow{MD}\vert} = \textcolor{#cc071e}{\vert\overrightarrow{ME}\vert}\).
\(A(5|5|0)\), \(E(2|0|4)\)
\[\overrightarrow{MD} = \overrightarrow{D} - \overrightarrow{M} = \begin{pmatrix} 5 \\ -5 \\ 0 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ m \end{pmatrix} = \begin{pmatrix} 5 \\ -5 \\ -m \end{pmatrix}\]
\[\overrightarrow{ME} = \overrightarrow{E} - \overrightarrow{M} = \begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ m \end{pmatrix} = \begin{pmatrix} 2 \\ 0 \\ 4 - m \end{pmatrix}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \textcolor{#cc071e}{\vert\overrightarrow{MD}\vert} &= \textcolor{#cc071e}{\vert\overrightarrow{ME}\vert} \\[0.8em] \left| \begin{pmatrix} 5 \\ -5 \\ -m \end{pmatrix} \right| &= \left| \begin{pmatrix} 2 \\ 0 \\ 4 - m \end{pmatrix} \right| \\[0.8em] \sqrt{5^{2} +(-5)^{2} + (-m)^{2}} &= \sqrt{2^{2} + 0^{2} + (4 - m)^{2}}&&| \; (\dots)^{2}\;\text{(Quadrieren)} \\[0.8em] 50 + m^{2} &= 4 + 16 - 8m + m^{2}&&| -m^{2} + 8m - 50 \\[0.8em] 8m &= -30&&| : (-30) \\[0.8em] m &= -3{,}75\end{align*}\]
\[\Rightarrow \enspace M(0|0|-3{,}75)\]


