An den betrachteten geraden Abschnitt der Achterbahn schließt sich - in Fahrtrichtung gesehen - eine Rechtskurve an, die im Modell durch einen Viertelkreis beschrieben wird, der in der Ebene \(E\) verläuft und den Mittelpunkt \(M \left( 0|3\sqrt{2}|2 \right)\) hat.
Das Lot von \(M\) auf \(g\) schneidet \(g\) im Punkt \(B\). Im Modell stellt \(B\) den Punkt der Achterbahn dar, in dem der gerade Abschnitt endet und die Kurve beginnt. Bestimmen Sie die Koordinaten von \(B\) und berechnen Sie den Kurvenradius im Modell.
(Teilergebnis: \(B\left( -1|2\sqrt{2}|3 \right)\))
(5 BE)
Lösung zu Teilaufgabe c
Koordinaten eines Lotfußpunktes, Abstand Punkt Gerade
\[M\,(0|3\sqrt{2}|2)\]
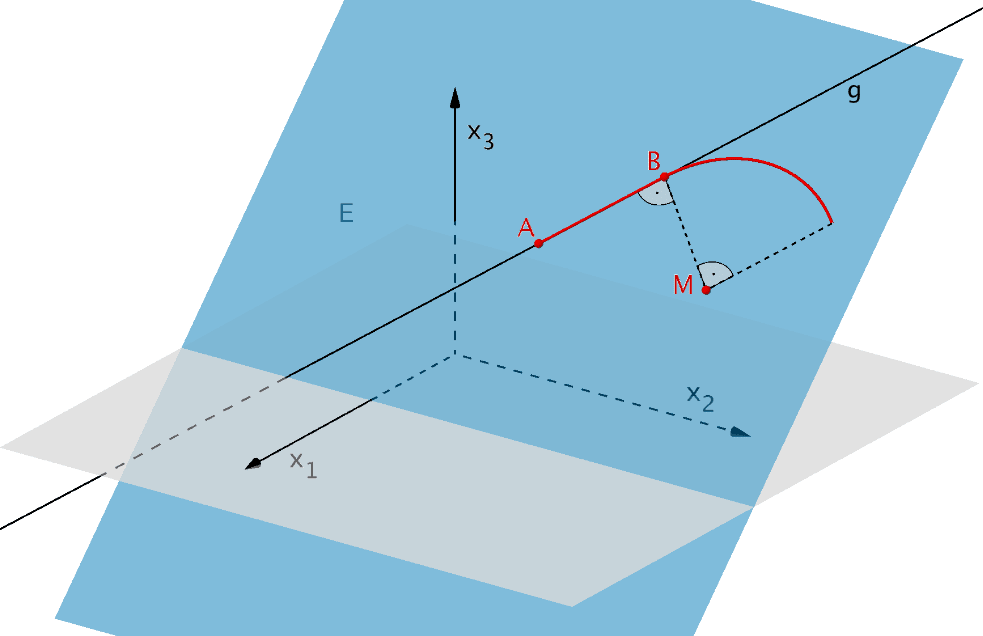
Lotfußpunkt \(B\) des Lotes von \(M\) auf die Gerade \(g\), Viertelkreisbogen mit Mittelpunkt \(M\), der im Punkt \(B\) an die Strecke \([AB]\) anschließt
Der Kurvenradius der Rechtskurve (des Viertelkreisbogens) ist gleich dem Abstand \(d(M;g)\) des Punktes \(M\) von der Geraden \(g\). Um diesen Abstand berechnen zu können, bestimmt man zunächst - wie in der Aufgabenstellung ohnehin gefordert - die Koordinaten des Lotfußpunktes \(B\) des Lotes von \(M\) auf die Gerade \(g\).
Berechnung der Koordinaten von \(B\)
1. Lösungsansatz mit Hilfsebene
2. Lösungsansatz: Anwenden des Skalarprodukts
1. Lösungsansatz mit Hilfsebene
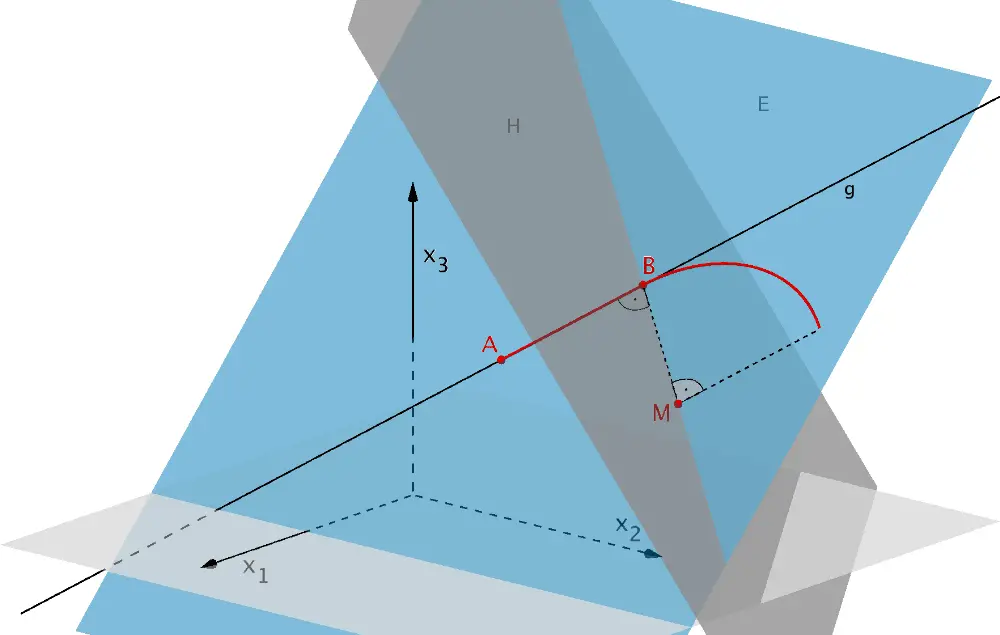
Die Hilfsebene \(H\) mit den Eigenschaften \(M \in H\) und \(H \perp g\) schneidet die Gerade \(g\) im Lotfußpunkt \(B\) des Lotes von \(M\) auf die Gerade \(g\).
Bestimmt man eine Hilfsebene \(H\), die senkrecht zur Geraden \(g\) liegt und den Punkt \(M\) enthält, so lassen sich die Koordinaten von \(B\) berechnen, indem man den Schnittpunkt der Geraden \(g\) mit der Hilfsebene \(H\) bestimmt.
Abstand Punkt - Gerade, Ansatz: Hilfsebene aufstellen
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
1. Hilfsebene \(H\) mit den Eigenschaften \(P \in H\) und \(H \perp g\) bestimmen:
\[H \colon \overrightarrow{n}_H \circ \left( \overrightarrow X - \overrightarrow P \right) = 0\,; \quad \overrightarrow{n}_H = \overrightarrow u\]
2. Schnittpunkt \(S\) der Ebene \(H\) mit der Geraden \(g\) ermitteln:
\(H \cap g \colon \overrightarrow{n}_H \circ \left( \overrightarrow A + \lambda \cdot \overrightarrow u - \overrightarrow P \right) = 0 \quad \Longrightarrow \quad\) Wert für Parameter \(\lambda\)
\[S \in g \colon \overrightarrow S = \overrightarrow A + \lambda \cdot \overrightarrow u\]
3. Länge der Strecke \([PS]\) berechnen:
\[d\,(P; g) = \overline{PS} = \vert \overrightarrow P - \overrightarrow S \vert\]
Gleichung der Hilfsebene \(H\) mit den Eigenschaften \(M \in H\) und \(H \perp g\) aufstellen:
\(g\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\,; \enspace \lambda \in \mathbb R\) (siehe Teilaufgabe a)
\[H \perp g \quad \Longrightarrow \quad \overrightarrow{n}_{H} = \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
\[M\,(0|3\sqrt{2}|2) \in H\]
Der Ansatz zur Bestimmung der Hilfsebene \(H\) kann mit der Normalenform in Vektordarstellung oder in Koordinatendarstellung erfolgen.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
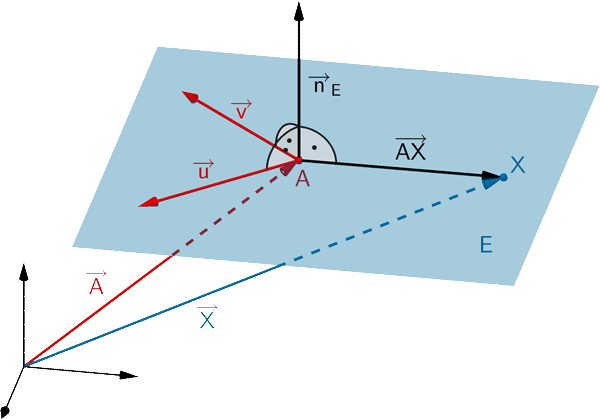
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Ansatz mit der Normalenform in Vektordarstellung:
\[\begin{align*} &H\colon \overrightarrow{n}_{H} \circ \left( \overrightarrow{X} - \overrightarrow{M} \right) = 0 \\[0.8em] &H\colon \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 3\sqrt{2} \\ 2 \end{pmatrix} \right] = 0 \end{align*}\]
Ansatz mit der Normalenform in Koordinatendarstellung:
\[\begin{align*} H\colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} &= 0 \\[0.8em] -x_{1} + \sqrt{2}x_{2} + x_{3} + n_{0} &= 0 \end{align*}\]
\[\begin{align*} M \in H\colon 0 + \sqrt{2} \cdot 3\sqrt{2} + 2 + n_{0} &= 0 \\[0.8em] 6 + 2 + n_{0} &= 0 \\[0.8em] 8 + n_{0} &= 0 & &| - 8 \\[0.8em] n_{0} &= -8 \end{align*}\]
\[\begin{align*} &H\colon -x_{1} + \sqrt{2}x_{2} + x_{3} - 8 = 0 \\[0.8em] &H\colon -x_{1} + \sqrt{2}x_{2} + x_{3} = 8 \end{align*}\]
Gerade \(g\) mit Hilfsebene \(H\) schneiden:
Je nachdem, welchen Ansatz man zur Bestimmung der Hilfsebene \(H\) gewählt hat, setzt man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Geradengleichung von \(g\) in die Ebenengleichung in Normalenform in Vektordarstellung oder in Koordinatendarstellung der Hilfsebene \(H\) ein und löst die Gleichung nach dem Parameter \(\lambda\) auf.
\[g\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
\[H\colon \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 3\sqrt{2} \\ 2 \end{pmatrix} \right] = 0\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*}g \cap H\colon \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} \circ \left[ \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} - \begin{pmatrix} 0 \\ 3\sqrt{2} \\ 2 \end{pmatrix} \right] &= 0 \\[0.8em] \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} \circ \left[ \begin{pmatrix} 0 \\ -2\sqrt{2} \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} \right] &= 0 \\[0.8em] (-1) \cdot (0 - \lambda) + \sqrt{2} \cdot (-2\sqrt{2} + \sqrt{2}\lambda) + 1 \cdot (0 + \lambda) &= 0 \\[0.8em] \lambda - 4 + 2\lambda + \lambda &= 0 \\[0.8em] 4\lambda - 4 &= 0 & &| + 4 \\[0.8em] 4\lambda &= 4 & &| : 4 \\[0.8em] \lambda &= 1 \end{align*}\]
oder
\[g\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
\[H\colon -x_{1} + \sqrt{2}x_{2} + x_{3} = 8\]
\[\begin{align*}g \cap H\colon -(0 - \lambda) + \sqrt{2} \cdot (\sqrt{2} + \sqrt{2}\lambda) + 2 + \lambda &= 8 \\[0.8em] \lambda + 2 + 2\lambda + 2 + \lambda &= 8 \\[0.8em] 4\lambda + 4 &= 8 & &| - 4 \\[0.8em] 4\lambda &= 4 & &| : 4 \\[0.8em] \lambda &= 1 \end{align*}\]
Koordinaten von \(B\) berechnen:
Für die Berechnung der Koordinaten des Lotfußpunktes \(B\) (Schnittpunkt der Geraden \(g\) mit der Hilfsebene \(H\)) wird der Parameterwert von \(\lambda\) in die Geradengleichung von \(g\) eingesetzt.
\[g\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
\[ \overrightarrow{B} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + 1 \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} = \begin{pmatrix} -1 \\ 2\sqrt{2} \\ 3 \end{pmatrix}\]
\[\Longrightarrow \quad B\,(-1|2\sqrt{2}|3)\]
2. Lösungsansatz: Anwenden des Skalarprodukts
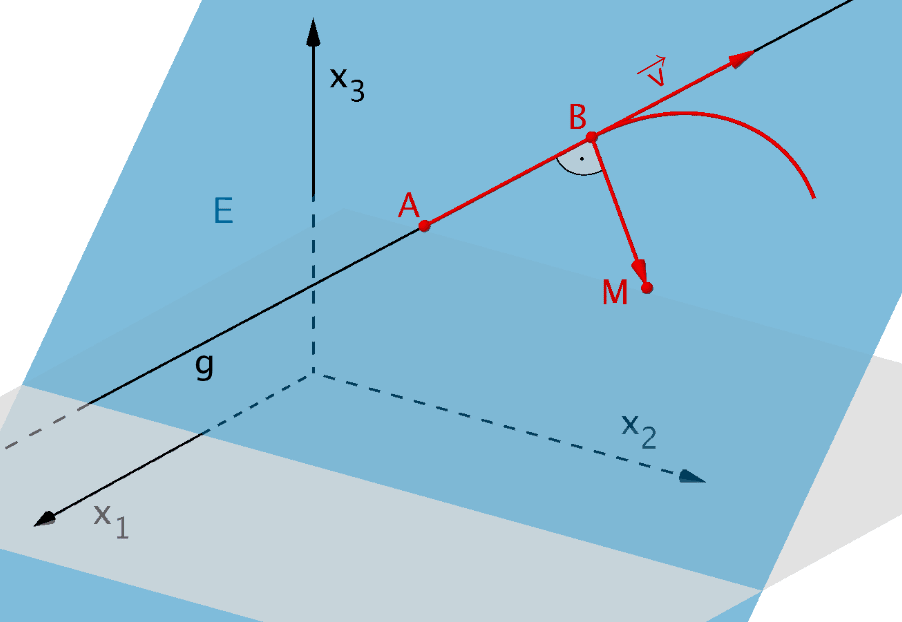
Der Richtungsvektor \(\overrightarrow{v}\) der Geraden \(g\) und der Vektor \(\overrightarrow{BM}\) stehen senkrecht zueinander.
Beschreibt man den Ortsvektor \(\overrightarrow{B}\) allgemein als einen Punkt auf der Geraden \(g\) und formuliert damit die Bedingung, dass das Skalarprodukt der beiden senkrecht zueinander stehenden Vektoren \(\overrightarrow{v}\) und \(\overrightarrow{BM}\) gleich Null ist, erhält man eine Gleichung für den Parameter \(\lambda\) der Geradengleichung von \(g\). Mit dem Parameterwert von \(\lambda\) lassen sich anschließend die Koordinaten von \(B\) berechnen.
Abstand Punkt - Gerade, Ansatz: Skalarprodukt anwenden
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(P\) auf die Gerade \(g\).
Somit gilt: \(\enspace \overrightarrow{FP} \perp \overrightarrow{u} \quad \Longleftrightarrow \quad \overrightarrow{FP} \circ \overrightarrow{u} = 0\)
1. Verbindungsvektor \(\overrightarrow{FP}\) allgemein beschreiben:
\[F \in g \colon \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow u \quad \Longrightarrow \quad \overrightarrow{FP} = \overrightarrow P - \left( \overrightarrow A + \lambda \cdot \overrightarrow u \right) \]
2. Koordinaten des Lotfußpunktes \(F\) bestimmen:
\[\overrightarrow{FP} \circ \overrightarrow{u} = 0 \quad \Longleftrightarrow \quad \left[ \overrightarrow P - \left( \overrightarrow A + \lambda \cdot \overrightarrow u \right) \right] \circ \overrightarrow u = 0\]
\(\Longrightarrow \quad\) Wert für Parameter \(\lambda\)
\[F \in g \colon \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow u\]
3. Länge der Strecke \([FP]\) berechnen:
\[d\,(P;g) = \overline{FP} = \vert \overrightarrow P - \overrightarrow F \vert\]
Vektor \(\overrightarrow{BM}\) allgemein beschreiben:
\[g\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
\[M\,(0|3\sqrt{2}|2)\]
\[B \in g \quad \Longrightarrow \quad \overrightarrow{B} = \begin{pmatrix} -\lambda \\ \sqrt{2} + \sqrt{2}\lambda \\ 2 + \lambda \end{pmatrix}\]
\[\begin{align*}\overrightarrow{BM} &= \overrightarrow{M} - \overrightarrow{B} \\[0.8em] &= \begin{pmatrix} 0 \\ 3\sqrt{2} \\ 2 \end{pmatrix} - \begin{pmatrix} -\lambda \\ \sqrt{2} + \sqrt{2}\lambda \\ 2 + \lambda \end{pmatrix} \\[0.8em] &= \begin{pmatrix} \lambda \\ 2\sqrt{2} - \sqrt{2}\lambda \\ -\lambda \end{pmatrix} \end{align*}\]
Skalarprodukt orthogonaler Vektoren anwenden:
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{v} \perp \overrightarrow{BM} \quad \Longleftrightarrow \quad \overrightarrow{v} \circ \overrightarrow{BM} = 0\]
\[\overrightarrow{v} = \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}; \quad \overrightarrow{BM} = \begin{pmatrix} \lambda \\ 2\sqrt{2} - \sqrt{2}\lambda \\ -\lambda \end{pmatrix}\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \overrightarrow{v} \circ \overrightarrow{BM} &= 0 \\[0.8em] \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} \circ \begin{pmatrix} \lambda \\ 2\sqrt{2} - \sqrt{2}\lambda \\ -\lambda \end{pmatrix} &= 0 \\[0.8em] (-1) \cdot \lambda + \sqrt{2} \cdot (2\sqrt{2} - \sqrt{2}\lambda) + 1 \cdot (-\lambda) &= 0 \\[0.8em] -\lambda + 4 - 2\lambda - \lambda &= 0 \\[0.8em] -4\lambda + 4 &= 0 & &| + 4\lambda \\[0.8em] 4 &= 4\lambda & &| : 4 \\[0.8em] 1 &= \lambda \end{align*}\]
Koordinaten von \(B\) berechnen:
Für die Berechnung der Koordinaten des Lotfußpunktes \(B\) wird der Parameterwert von \(\lambda\) in die Geradengleichung von \(g\) eingesetzt.
\[g\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
\[ \overrightarrow{B} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + 1 \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} = \begin{pmatrix} -1 \\ 2\sqrt{2} \\ 3 \end{pmatrix}\]
\[\Longrightarrow \quad B\,(-1|2\sqrt{2}|3)\]
3. Lösungsansatz: Lotgerade zur Geraden \(g\) durch den Punkt \(M \in E\)
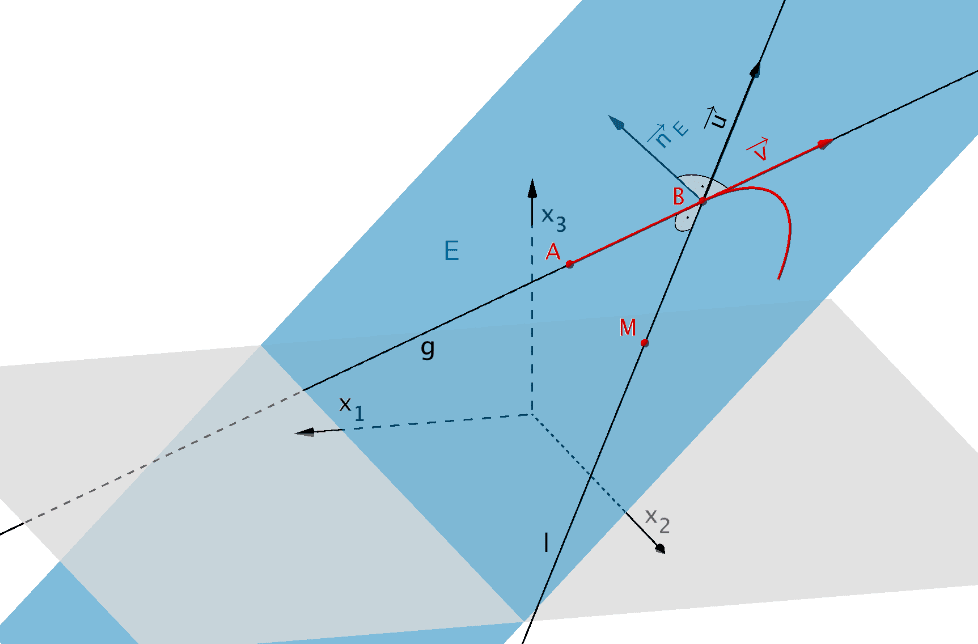
Die Lotgerade \(l\) zur Geraden \(g\) durch den Punkt \(M \in E\) schneidet die Gerade \(g\) im Lotfußpunkt \(B\) des Lotes von \(M\) auf die Gerade \(g\).
Gleichung der Lotgeraden \(l\):
Es sei \(\overrightarrow{u}\) der Richtungsvektor der Lotgeraden \(l\).
\[M\,(0|3\sqrt{2}|2) \in l\,, \enspace \overrightarrow{u} \perp \overrightarrow{v}\]
\[l\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 3\sqrt{2} \\ 2 \end{pmatrix} + \mu \cdot \overrightarrow{u}\]
Richtungsvektor \(\overrightarrow{u}\) der Lotgeraden \(l\) bestimmen:
Das Vektorprodukt aus dem Richtungsvektor \(\overrightarrow{v}\) der Geraden \(g\) und dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) ergibt einen Vektor, der senkrecht zu \(\overrightarrow{v}\) und senkrecht zu \(\overrightarrow{n}_{E}\) ist.
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\(\overrightarrow{v} = \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}, \enspace \overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}\) (siehe Teilaufgabe a,b)
\[\begin{align*} \overrightarrow{v} \times \overrightarrow{n}_{E} &= \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} \times \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} \sqrt{2} & \cdot & 1 & - & 1 & \cdot & 0 \\ 1 & \cdot & 1 & - & (-1) & \cdot & 1 \\ (-1) & \cdot & 0 & - & \sqrt{2} & \cdot & 1 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} \sqrt{2} \\ 2 \\ -\sqrt{2} \end{pmatrix} \\[0.8em] &= \sqrt{2} \cdot \begin{pmatrix} 1 \\ \sqrt{2} \\ -1 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} 1 \\ \sqrt{2} \\ -1 \end{pmatrix}\]
\[\Longrightarrow \quad l\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 3\sqrt{2} \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ \sqrt{2} \\ -1 \end{pmatrix}\]
Schnittpunkt der Lotgerade \(l\) und der Geraden \(g\) (Lotfußpunkt \(B\)) ermitteln:
Für die Berechnung des Schnittpunkts werden die Terme der beiden Geradengleichungen gleichgesetzt. Daraus ergibt sich ein überbestimmtes lineares Gleichungssystem mit drei linearen Gleichungen für die beiden zu bestimmenden Parameter \(\lambda\) und \(\mu\).
\[l\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 3\sqrt{2} \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ \sqrt{2} \\ -1 \end{pmatrix}\]
\[g\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
\[l \cap g\colon \begin{pmatrix} 0 \\ 3\sqrt{2} \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ \sqrt{2} \\ -1 \end{pmatrix} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
Lineares Gleichungssystem aufstellen und lösen:
\[\begin{align*} \text{I} & & & & \mu &= -\lambda \\[0.8em] \text{II} & & &\wedge & 3\sqrt{2} + \sqrt{2}\mu &= \sqrt{2} + \sqrt{2}\lambda \\[0.8em] \text{III} & & & \wedge & 2 - \mu &= 2 + \lambda \end{align*}\]
\[\begin{align*}\text{I in II}\colon \; 3\sqrt{2} - \sqrt{2}\lambda &= \sqrt{2} + \sqrt{2}\lambda & &| - \sqrt{2} \enspace + \sqrt{2}\lambda \\[0.8em] 2\sqrt{2} &= 2\sqrt{2}\lambda & &| : 2\sqrt{2} \\[0.8em] 1 &= \lambda \end{align*}\]
\[\lambda = 1 \;\text{in I}\colon \; \mu = -1\]
\[\begin{align*}\lambda = 1\,, \enspace \mu = -1 \:\text{in III}\colon \; 2 - (-1) &= 2 + 1 \\[0.8em] 3 &= 3 \quad (\text{w}) \end{align*}\]
Anmerkung: Da Gleichung I und Gleichung III zueinander äquivalent sind, ist das Überprüfen der wahren Aussage von Gleichung III in diesem Fall überflüssig.
Koordinaten von \(B\) berechnen:
Für die Berechnung der Koordinaten des Lotfußpunktes \(B\) wird entweder der Parameterwert von \(\lambda\) in die Geradengleichung von \(g\) oder der Parameterwert von \(\mu\) in die Geradengleichung von \(l\) eingesetzt.
\[g\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
\[l\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 3\sqrt{2} \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ \sqrt{2} \\ -1 \end{pmatrix}\]
\[ \overrightarrow{B} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + 1 \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} = \begin{pmatrix} -1 \\ 2\sqrt{2} \\ 3 \end{pmatrix}\]
\[\Longrightarrow \quad B\,(-1|2\sqrt{2}|3)\]
oder
\[ \overrightarrow{B} = \begin{pmatrix} 0 \\ 3\sqrt{2} \\ 2 \end{pmatrix} - 1 \cdot \begin{pmatrix} 1 \\ \sqrt{2} \\ -1 \end{pmatrix} = \begin{pmatrix} -1 \\ 2\sqrt{2} \\ 3 \end{pmatrix}\]
\[\Longrightarrow \quad B\,(-1|2\sqrt{2}|3)\]
Berechnung des Kurvenradius
Der Kurvenradius \(r\) der Rechtskurve (des Viertelkreisbogens) ist gleich dem Abstand \(d(M;g)\) des Punktes \(M\) von der Geraden \(g\). Dieser ist gleich der Länge der Strecke \([MB]\), welche der Mittelpunkt \(M\) des Viertelkreises und der Lotfußpunkt \(B\) des Lotes von \(M\) auf die Gerade \(g\) festlegen.
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\overrightarrow{B} = \begin{pmatrix} -1 \\ 2\sqrt{2} \\ 3 \end{pmatrix}, \enspace \overrightarrow{M} = \begin{pmatrix} 0 \\ 3\sqrt{2} \\ 2 \end{pmatrix}\]
\[\begin{align*} r = d\,(M;g) &= \overline{MB} \\[0.8em] &= \vert \overrightarrow{MB} \vert \\[0.8em] &= \vert \overrightarrow{B} - \overrightarrow{M} \vert \\[0.8em] &= \left| \begin{pmatrix} -1 \\ 2\sqrt{2} \\ 3 \end{pmatrix} - \begin{pmatrix} 0 \\ 3\sqrt{2} \\ 2 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} -1 \\ -\sqrt{2} \\ 1 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-1)^{2} + (-\sqrt{2})^{2} + 1^{2}} \\[0.8em] &= \sqrt{4} \\[0.8em] &= 2 \end{align*}\]

