Geben Sie \(f(8)\) an und zeichnen Sie \(G_f\) unter Berücksichtigung der bisherigen Ergebnisse in ein Koordinatensystem ein.
(4 BE)
Lösung zu Teilaufgabe f
\[f(x) = 2 \cdot \sqrt{10x - x^2}; \; D_{f} = [0;10]\]
\[f(8) = 2 \cdot \sqrt{10 \cdot 8 - 8^2} = 2 \cdot \sqrt{16} = 2 \cdot 4 = 8\]
Bisherige Ergebnisse:
- \(G_f\) besitzt die Nullstellen \(x = 0\) und \(x = 10\) (vgl. Teilaufgabe a).
- \(G_f\) hat den Hochpunkt \((5|10)\) (vgl. Teilaufgabe b).
- \(G_f\) ist in \(D_f = [0;10]\) rechtsgekrümmt (vgl. Teilaufgabe c).
- Die Gerade mit der Gleichung \(x = 5\) ist Symmetrieachse von \(G_f\) (vgl. Teilaufgabe d).
- \(G_f\) hat im Ursprung eine senkrechte Tangente (\(y\)-Achse) (vgl. Teilaufgabe e).
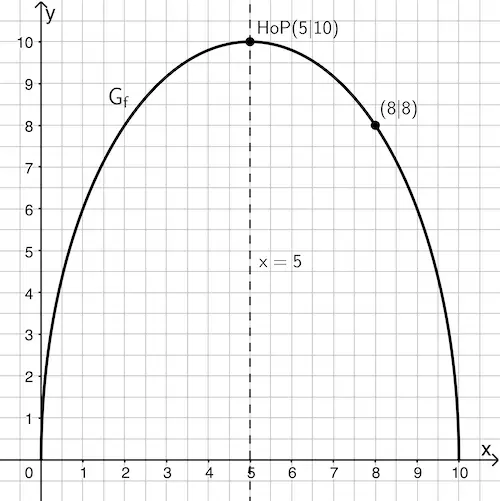
Graph der Funktion \(f\colon x\mapsto 2 \cdot \sqrt{10x - x^2}\) mit Hochpunkt \((5|10)\) und der Gerade mit der Gleichung \(x = 5\) als Symmetrieachse


