Die in \(\mathbb R\) definierte Funktion \(g\) ist gegeben durch \(g(x) = a \cdot f(x) + b \cdot x\) mit reellen Zahlen \(a\) und \(b\). Die Punkte \((0|-3)\) und \(\big(\frac{\pi}{2}| \frac{3}{4}\pi \big)\) liegen auf dem Graphen von \(g\). Ermitteln Sie \(a\) und \(b\).
(4 BE)
Lösung zu Teilaufgabe 3b
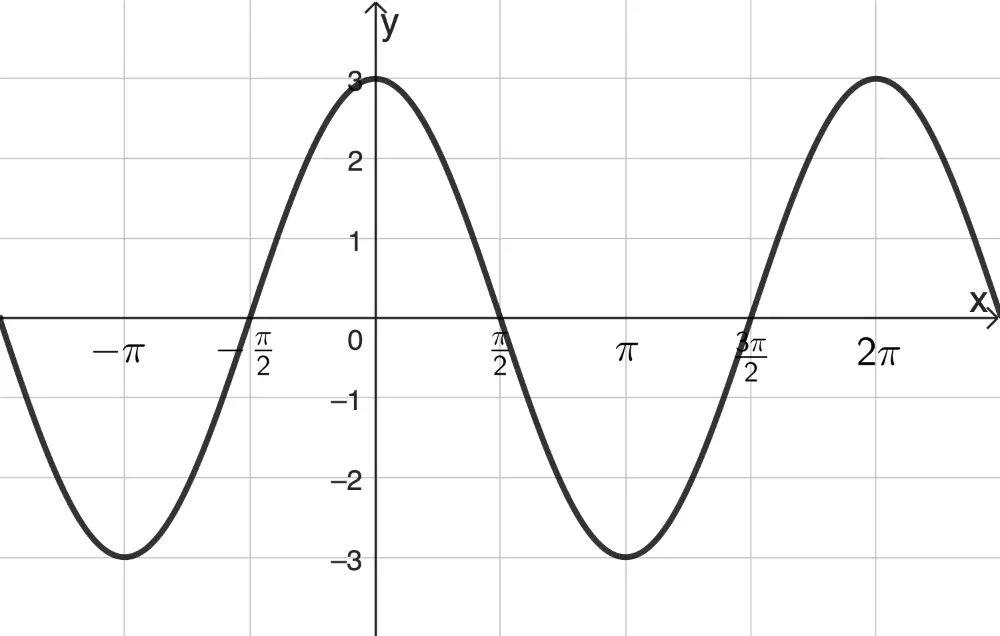Abb. 1
\[g(x) = a \cdot f(x) + b \cdot x; \; D_g = \mathbb R\]
Die Werte von \(a\) und \(b\) lassen sich durch Einsetzen der Koordinaten der Punkte \((0|-3)\) und \(\big(\frac{\pi}{2}| \frac{3}{4}\pi \big)\) in den Funktionsterm von \(g\) ermitteln, in diesem Fall ohne ein Gleichungssystem lösen zu müssen. Die Funktionswerte \(f(0)\) und \(f(\frac{\pi}{2})\) können der Abbildung 1 entnommen werden.
\((0|-3)\) eingesetzt:
\[\begin{align*} a \cdot f(0) + b \cdot 0 &= -3 &&| \; f(0) = 3\; \text{(vgl. Abb. 1)} \\[0.8em] a \cdot 3 &= -3 &&| : 3 \\[0.8em] a &= -1 \end{align*}\]
\(\big(\frac{\pi}{2}| \frac{3}{4}\pi \big)\) eingesetzt:
\[\begin{align*} a \cdot f\big(\textstyle \frac{\pi}{2}\big) + b \cdot \displaystyle \frac{\pi}{2} &= \frac{3}{4}\pi &&| \;f\big(\textstyle \frac{\pi}{2}\big) = 0 \; \text{(vgl. Abb. 1)} \\[0.8em] a \cdot 0 + b \cdot \frac{\pi}{2} &= \frac{3}{4}\pi &&| \cdot \frac{2}{\pi} \\[0.8em] b &= \frac{3}{2}\end{align*}\]
