- Details
- Kategorie: Analysis 1
Gegeben ist die Funktion \(\displaystyle f \, \colon x \mapsto \frac{x}{\ln x}\) mit Definitionsmenge \(\mathbb R^+ \, \backslash \{1\}\). Bestimmen Sie Lage und Art des Extrempunkts des Graphen von \(f\).
(5 BE)
- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f\) mit \(f(x) = e^x \cdot \left( 2x + x^2 \right)\).
Bestimmen Sie die Nullstellen der Funktion \(f\).
(2 BE)
- Details
- Kategorie: Analysis 1
Zeigen Sie, dass die in \(\mathbb R\) definierte Funktion \(F\) mit \(F(x) = x^2 \cdot e^x\) eine Stammfunktion von \(f\) ist. Geben eine Gleichung einer weiteren Stammfunktion \(G\) von \(f\) an, für die \(G(1) = 2e\) gilt.
(3 BE)
- Details
- Kategorie: Analysis 1
Gegeben sind die in \(\mathbb R\) definierten Funktionen \(g_{a,c} \, \colon x \mapsto \sin (ax) + c\) mit \(a,c \in \mathbb R^+_0\).
Geben Sie für jede der beiden folgenden Eigenschaften einen möglichen Wert für \(a\) und einen möglichen Wert für \(c\) so an, dass die zugehörige Funktion \(g_{a,c}\) diese Eigenschaft besitzt.
α) Die Funktion\(g_{a,c}\) hat die Wertemenge \([0;2]\).
β) Die Funktion \(g_{a,c}\) hat im Intervall \([0;\pi]\) genau drei Nullstellen.
(3 BE)
- Details
- Kategorie: Analysis 1
Ermitteln Sie in Abhängigkeit von \(a\), welche Werte die Ableitung von \(g_{a,c}\) annehmen kann.
(2 BE)
- Details
- Kategorie: Analysis 1
Die Abbildung zeigt den Graphen einer Funktion \(f\).
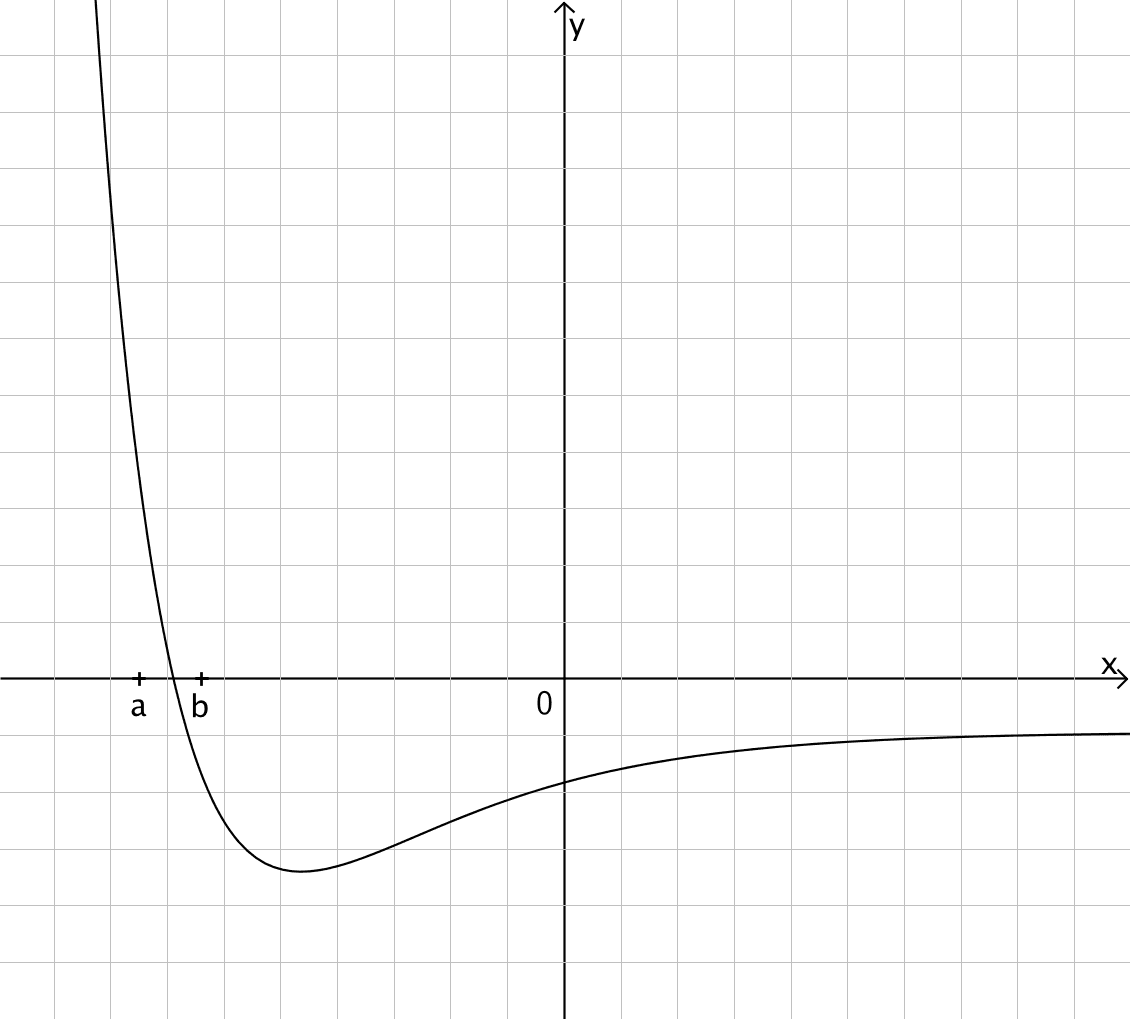
Beschreiben Sie für \(a \leq x \leq b\) den Verlauf des Graphen einer Stammfunktion von \(f\).
(2 BE)
- Details
- Kategorie: Analysis 1
Skizzieren Sie in der Abbildung den Graphen einer Stammfunktion von \(f\) im gesamten dargestellten Bereich.
(3 BE)


