Der Polstab wird im Modell durch die Strecke \([MS]\) mit \(S\,(4{,}5|0|4{,}5)\) dargestellt. Zeigen Sie, dass der Polstab senkrecht auf der Grundplatte steht, und berechnen Sie die Länge des Polstabs auf Zentimeter genau.
(3 BE)
Lösung zu Teilaufgabe c
Parallelität zweier Vektoren
\[S\,(4{,}5|0|4{,}5)\]
Nachweis, dass der Polstab senkrecht auf der Grundplatte steht
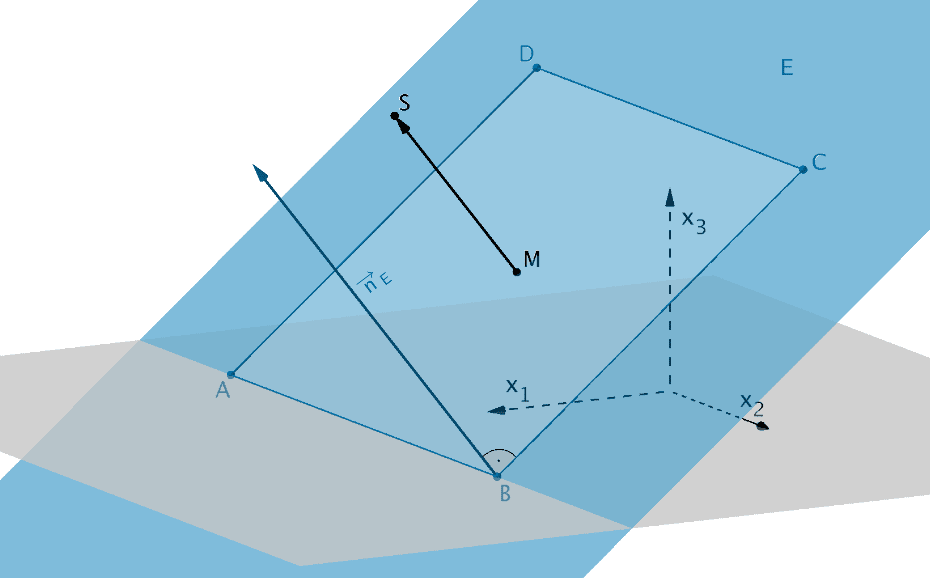
Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) und Vektor \(\overrightarrow{MS}\)
Der Polstab steht senkrecht auf der Grundplatte (Rechteck \(ABCD\)), wenn die Strecke \([MS]\) senkrecht auf der Ebene \(E\) steht. Dies ist dann der Fall, wenn der Vektor \(\overrightarrow{MS}\) parallel zum Normalenvektor \(\overrightarrow{n}_{E}\) (siehe Teilaufgabe a) der Ebene \(E\) ist. Um die Parallelität der beiden Vektoren nachzuweisen, zeigt man, dass die Vektoren linear abhängig sind, dass also gilt:
Lineare (Un-)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} = k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} \neq k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
Bei der Untersuchung der linearen (Un)Abhängigkeit dreier Vektoren spielt es keine Rolle, welche der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) oder \(\overrightarrow{c}\) man als Linearkombination der beiden anderen Vektoren darzustellen versucht.
\[\overrightarrow{MS} = k \cdot \overrightarrow{n}_{E}\,; \enspace k \in \mathbb R\]
\[S\,(4{,}5|0|4{,}5)\,, \enspace M\,(2{,}5|0|2)\,, \enspace \overrightarrow{n}_{E} = \begin{pmatrix} 4 \\ 0 \\ 5 \end{pmatrix}\]
\[\overrightarrow{MS} = \overrightarrow{S} - \overrightarrow{M} = \begin{pmatrix} 4{,}5 \\ 0 \\ 4{,}5 \end{pmatrix} - \begin{pmatrix} 2{,}5 \\ 0 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 0 \\ 2{,}5 \end{pmatrix}\]
\[\Longrightarrow \quad \overrightarrow{MS} = \frac{1}{2} \cdot \overrightarrow{n}_{E} \quad \Longrightarrow \quad \overrightarrow{MS} \parallel \overrightarrow{n}_{E}\]
\(\Longrightarrow \quad \overrightarrow{MS} \perp E\) bzw. \([MS] \perp E\)
Der Polstab steht senkrecht auf der Grundplatte.
Länge des Polstabs
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{MS} &= \vert \overrightarrow{MS} \vert \\[0.8em] &= \left| \begin{pmatrix} 2 \\ 0 \\ 2{,}5 \end{pmatrix} \right| \\[0.8em] &= \sqrt{2^{2} + 0^{2} + 2{,}5^{2}} \\[0.8em] &= \frac{\sqrt{41}}{2} \\[0.8em] &\approx 3{,}2 \end{align*}\]
\(1\;\sf{LE}\) (Längeneinheit) \(\mathrel{\hat=} 10\;\sf{cm}\) (siehe Angabe)
\[3{,}2\;\sf{LE} \mathrel{\hat=} (10 \cdot 3{,}2)\; \sf{cm} = 32 \;\sf{cm}\]
Der Polstab ist ca. 32 cm lang.
