Für welche Füllhöhen \(x\) liegt der Schwerpunkt \(S\) höchstens 5 cm hoch? Beantworten Sie diese Frage zunächst näherungsweise mithilfe von Abbildung 2 und anschließend durch Rechnung.
(6 BE)
Lösung zu Teilaufgabe 3c
\[f(x) = \frac{1}{2}x - \frac{1}{2} + \frac{8}{x + 1}\,; \quad 0 \leq x \leq 15\]
Graphische Lösung
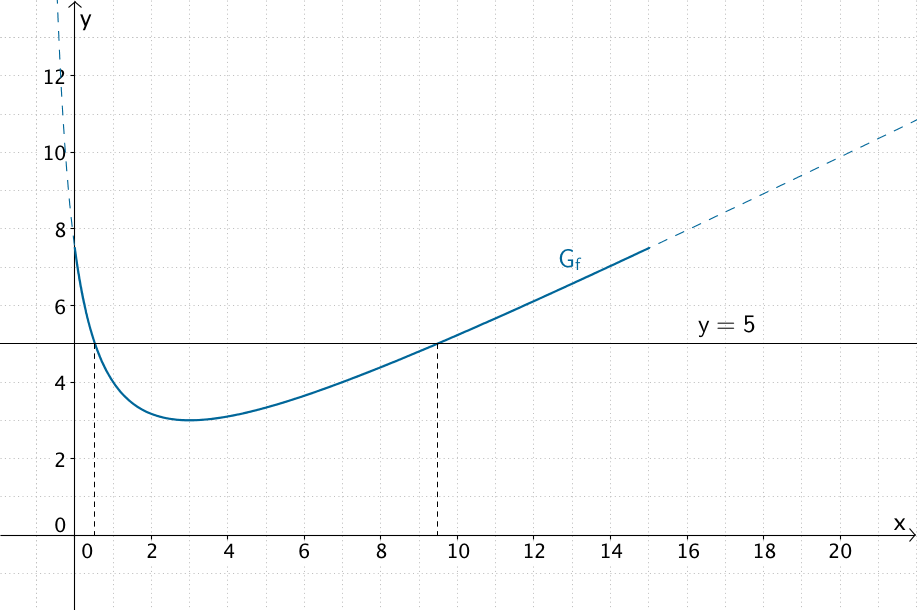
Die \(x\)-Koordinaten der Schnittpunkte zwischen \(G_f\) und der Geraden \(y = 5\) legen das Intervall für die Füllhöhen \(x\) fest, für die der Schwerpunkt \(S\) höchstens 5 cm hoch liegt.
Im Rahmen der Ablesegenauigkeit entnimmt man für \(f(x) \leq 5\,\):
\[0{,}5 \leq x \leq 9{,}5\]
Für die Füllhöhen \(0{,}5 \leq x \leq 9{,}5\) liegt der Schwerpunkt \(S\) höchstens 5 cm hoch.
Rechnerische Lösung
\[f(x) = \frac{1}{2}x - \frac{1}{2} + \frac{8}{x + 1}\,; \quad 0 \leq x \leq 15\]
\[\begin{align*} f(x) &\leq 5 \\[0.8em] \frac{1}{2}x - \frac{1}{2} + \frac{8}{x + 1} &\leq 5 & &| +\frac{1}{2} \\[0.8em] \frac{1}{2}x + \frac{8}{x + 1} &\leq 5{,}5 & &| \cdot 2 \\[0.8em] x + \frac{16}{x + 1} &\leq 11 & &| \cdot (x + 1) \\[0.8em] x(x + 1) + 16 &\leq 11(x +1) \\[0.8em] x^2 + x + 16 &\leq 11x + 11 & &| -11x - 11 \\[0.8em] x^2 - 10x + 5 &\leq 0 \end{align*}\]
Zur Lösung der quadratischen Ungleichung wird der quadratische Term als Produkt zweier Linearfaktoren formuliert. Dafür löst man zunächst die quadratische Gleichung \(x^2 - 10x + 5 = 0\).
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*} x_{1,2} &= \frac{10 \pm \sqrt{(-10)^2 - 4 \cdot 1 \cdot 5}}{2 \cdot 1} \\[0.8em] &= \frac{10 \pm \sqrt{80}}{2} \\[0.8em] &= \frac{10 \pm 4\sqrt{5}}{2} \\[0.8em] &= 5 \pm 2\sqrt{5} \end{align*}\]
\[x_1 = 5 - 2\sqrt{5} \enspace \vee \enspace x_2 = 5 + 2\sqrt{5}\]
Quadratische Ungleichung als Produkt zweier Linearfaktoren formulieren:
\[\begin{align*}x^2 - 10x + 5 &\leq 0 \\[0.8em] \left[ x - (5 - 2\sqrt{5}) \right] \cdot \left[ x - (5 + 2\sqrt{5}) \right] &\leq 0 \end{align*}\]
Zwei Fälle unterscheiden:
1. Fall:
\[\begin{align*} x - (5- 2\sqrt{5}) &\geq 0 & &\wedge & x - (5 + 2\sqrt{5}) &\leq 0 \\[0.8em] x &\geq 5 - 2\sqrt{5} & &\wedge & x &\leq 5 + 2\sqrt{5} \\[0.8em] x &\gtrapprox 0{,}53 & &\wedge & x &\lessapprox 9{,}47 \end{align*}\]
\[\Longrightarrow \quad x \in [5 - 2\sqrt{5}; 5 + 2\sqrt{5}]\]
Für Füllhöhen \(x\) mit \(x \in [5 - 2\sqrt{5}; 5 + 2\sqrt{5}]\) liegt der Schwerpunkt \(S\) höchstens 5 cm hoch.
2. Fall:
\[\begin{align*} x - (5- 2\sqrt{5}) &\leq 0 & &\wedge & x - (5 + 2\sqrt{5}) &\geq 0 \\[0.8em] x &\leq 5 - 2\sqrt{5} & &\wedge & x &\geq 5 + 2\sqrt{5} \\[0.8em] x &\lessapprox 0{,}53 & &\wedge & x &\gtrapprox 9{,}47 \end{align*}\]
\(\Longrightarrow \quad\) keine Lösung
Alternative graphisch-rechnerische Lösung
Als teilweise graphische Alternative, ohne die Ungleichung lösen zu müssen, können zunächst die Nullstellen \(x_{1} = 5 - 2\sqrt{5}\) und \(x_{2} = 5 +2\sqrt{5}\) der Funktion \(x \mapsto x^{2} - 10x + 5\) mithilfe der Lösungsformel für quadratische Gleichungen berechnet werden (siehe oben). Anschließend skizziert man die nach oben geöffnete Parabel dieser Funktion (Skizze genügt!) und kennzeichnet die Nullstellen sowie den Bereich \(]x_{1};x_{2}[\,\), in dem die Parabel unterhalb der \(x\)-Achse verläuft.
Schlussfolgerung: \(x^2 - 10x + 5 \leq 0\) für \(x \in [5 - 2\sqrt{5}; 5 + 2\sqrt{5}]\)
Für Füllhöhen \(x\) mit \(x \in [5 - 2\sqrt{5}; 5 + 2\sqrt{5}]\) liegt der Schwerpunkt \(S\) höchstens 5 cm hoch.
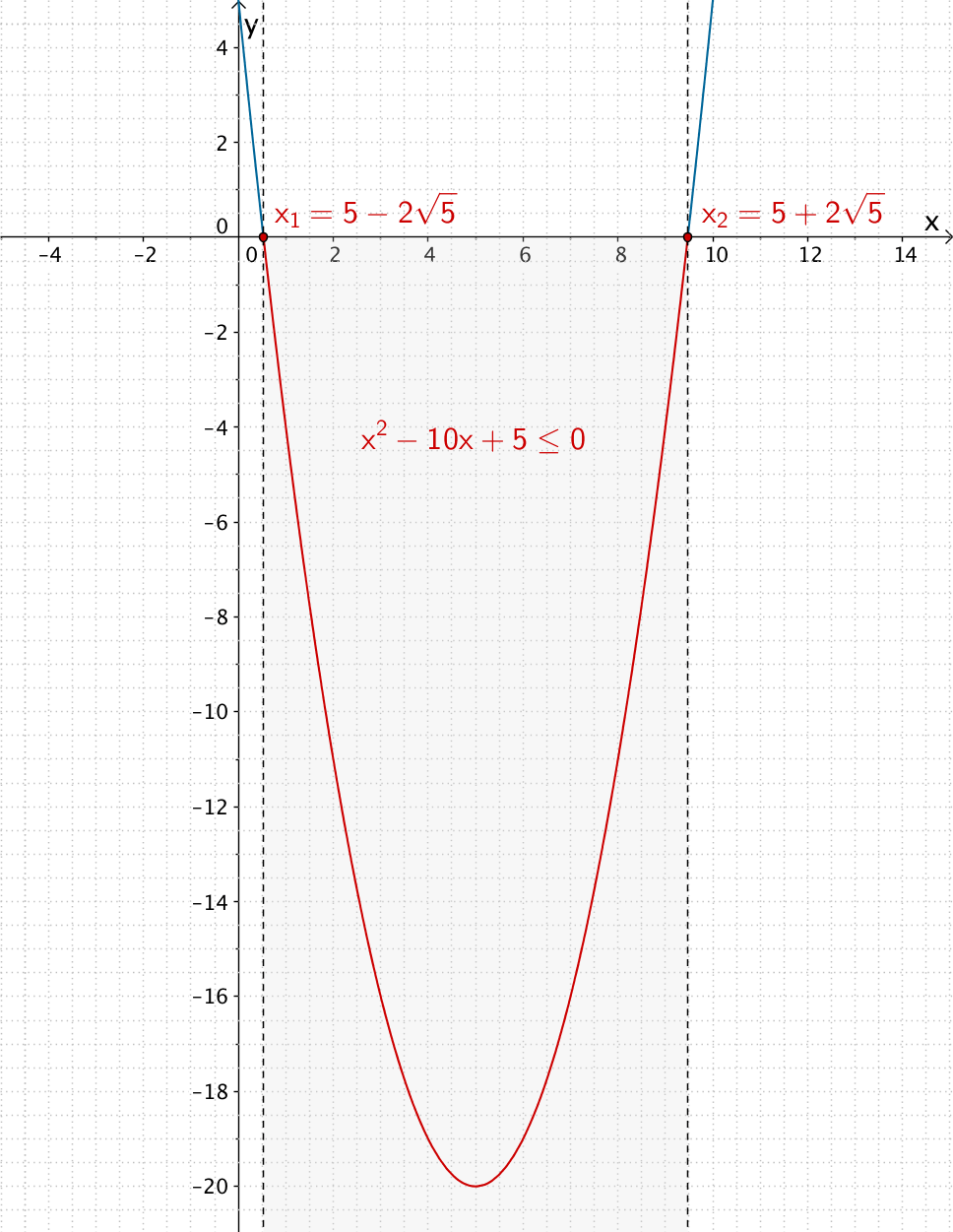
Parabel der Funktion \(x \mapsto x^{2} - 10x + 5\) sowie Nullstellen \(x_{1} = 5-2\sqrt{5}\) und \(x_{2} = 5 +2\sqrt{5}\)


