Zeigen Sie, dass für den Erwartungswert \(E(X)\) der Zufallsgröße \(X\) gilt: \(E(X) = 9p^2 + 12p + 4\).
(3 BE)
Lösung zu Teilaufgabe 1b
Erwartungswert einer Zufallsgröße bestimmen
Ergebnis aus Teilaufgabe 1a: \(P(X = 10) = 2p - 2p^{2}\)
Mithilfe des Baumdiagramms und dem Ergebnis aus Teilaufgabe 1a lässt sich die Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) beschreiben.
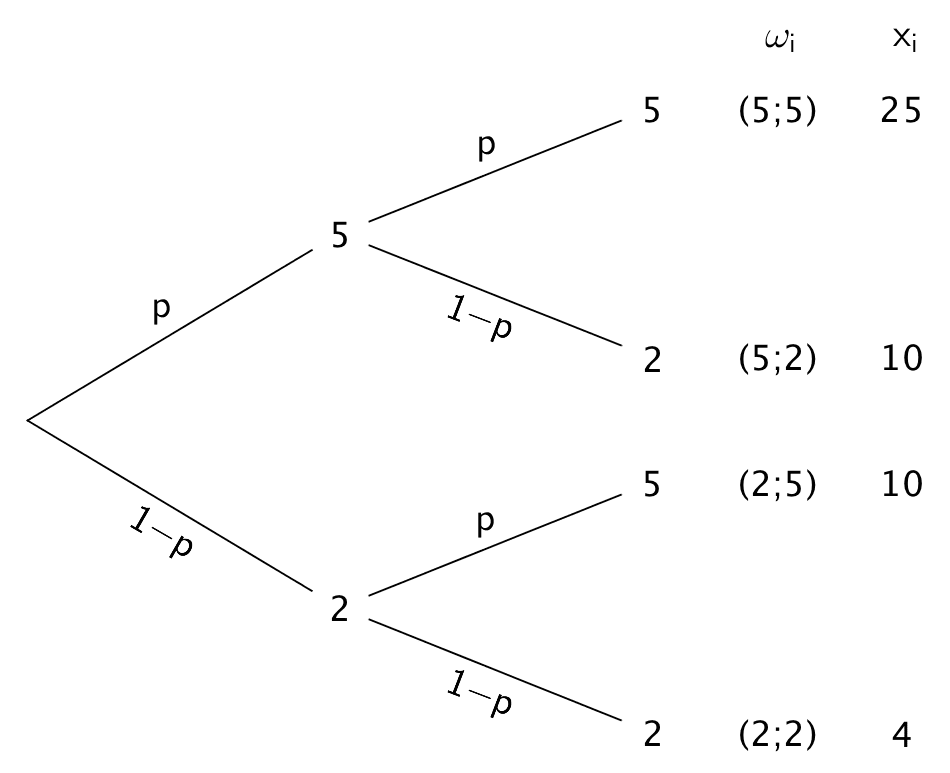
Baumdiagramm für zweimaliges Drehen des Glücksrads (zweistufiges Zufallsexperiment) mit Elementarereignissen \(\omega_{i}\) und Werten \(x_{i}\) der Zufallsgröße \(X\)
Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\):
\[P(X = 4) = P(2;2) = (1 - p)^{2}\]
\[P(X = 25) = P(5;5) = p^{2}\]
| \(X = x_{i}\) | \(4\) | \(10\) | \(25\) |
| \(P(X = x_{i})\) | \((1 - p)^{2}\) | \(2p - 2p^{2}\) | \(p^{2}\) |
Erwartungswert \(E(X)\) der Zufallsgröße \(X\) ermitteln:
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(\boldsymbol{X}\)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot P(X = x_i) \\[0.8em] &= x_{1} \cdot P(X = x_1) + x_{2} \cdot P(X = x_2) + \cdots + x_{n} \cdot P(X = x_n) \end{align*}\]
Der Erwartungswert \(\mu = E(X)\) gibt den Mittelwert einer Zufallsgröße \(X\) pro Versuch an, der bei sehr häufiger Durchführung eines Zufallsexperiments (auf lange Sicht) zu erwarten ist.
\[\begin{align*} E(X) &= 4 \cdot (1 - p)^{2} + 10 \cdot (2p - 2p^{2}) + 25 \cdot p^{2} \\[0.8em] &= 4 \cdot (1 - 2p + p^{2}) + 20p - 20p^{2} + 25p^{2} \\[0.8em] &= 4 - 8p +4p^{2} + 20p +5p^{2} \\[0.8em] &= 9p^{2} + 12p + 4 \end{align*}\]


