Neben dem Fußballturnier werden für die Schülerinnen und Schüler auch ein Elfmeterschießen und ein Torwandschießen angeboten.
Dafür konnten sich Kinder in zwei Listen eintragen. 45 % der Kinder haben sich sowohl für das Torwandschießen als auch für das Elfmeterschießen eingetragen, 15 % haben sich nur für das Elfmeterschießen eingetragen. 90 % der Kinder, die sich für das Torwandschießen eingetragen haben, haben sich auch für das Elfmeterschießen eingetragen. Aus den Kindern wird eines zufällig ausgewählt. Betrachtet werden die folgenden Ereignisse:
\(T\): „Das Kind hat sich für das Torwandschießen eingetragen."
\(E\): „das Kind hat sich für das Elfmeterschießen eingetragen."
Untersuchen Sie die Ereignisse \(T\) und \(E\) auf stochastiche Unabhängigkeit.
(4 BE)
Lösung zu Teilaufgabe 2a
Gegeben: \(P(T \cap E) = 0{,}45\), \(P(\overline{T} \cap E) = 0{,}15\), \(P_{T}(E) = 0{,}9\)
Stochastische (Un)Abhängigkeit von zwei Ereignissen
Zwei Ereignisse \(A\) und \(B\) heißen stochastisch unabhängig, wenn
\(P(A) \cdot P(B) = P(A \cap B)\) gilt. (vgl. Merkhilfe) *
Andernfalls heißen die Ereignisse \(A\) und \(B\) stochastisch abhängig.
Sind zwei Ereignisse \(A\) und \(B\) stochastisch unabhängig, beeinflusst das Eintreten des Ereignisses \(A\) nicht das Eintreten des Ereignisses \(B\) und umgekehrt.
* Oder wenn
\(P(\overline{A}) \cdot P(B) = P(\overline{A} \cap B)\) bzw.
\(P(A) \cdot P(\overline{B}) = P(A \cap \overline{B})\) bzw.
\(P(\overline{A}) \cdot P(\overline{B}) = P(\overline{A} \cap \overline{B})\) gilt.
Die Ereignisse \(T\) und \(E\) sind stochastisch unabhängig, wenn beispielsweise \(P(T \cap E) = P(T) \cdot P(E)\) gilt.
\[\begin{align*}P(E) &= P(T \cap E) + P(\overline{T} \cap E) \\[0.8em] &= 0{,}45 + 0{,}15 \\[0.8em] &= 0{,}6 \end{align*}\]
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[\begin{align*} P_{T}(E) &= \frac{P(T \cap E)}{P(T)} \\[0.8em] \Leftrightarrow \enspace P(T) &= \frac{P(T \cap E)}{P_{T}(E)} \\[0.8em] &= \frac{0{,}45}{0{,}9} = 0{,}5 \end{align*}\]
\[P(T) \cdot P(E) = 0{,}6 \cdot 0{,}5 = 0{,}3 \textcolor{#cc071e}{\neq} 0{,}45 = P(T \cap E)\]
Die Ereignisse \(T\) und \(E\) sind stochastisch abhängig.
Ausführliche Erklärung (nicht verlangt)
Ein Baumdiagramm gestaltet die Aufgabenstellung übersichtlich.
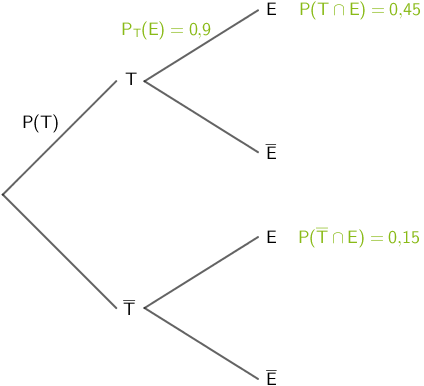
Baumdiagramm mit gegebenen Wahrscheinlichkeiten
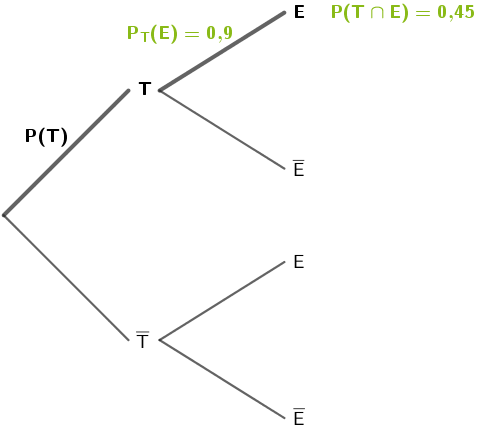
Die Wahrscheinlichkeit \(P(T)\) lässt sich mithilfe der 1. Pfadregel berechnen.
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}P(T) \cdot \textcolor{#89ba17}{P_{T}(E)} &= \textcolor{#89ba17}{P(T \cap E)} &&| : P_{T}(E) \\[0.8em] P(T) &= \frac{P(T \cap E)}{P_{T}(E)} \\[0.8em] &= \frac{0{,}45}{0{,}9} \\[0.8em] &= 0{,}5 \end{align*}\]
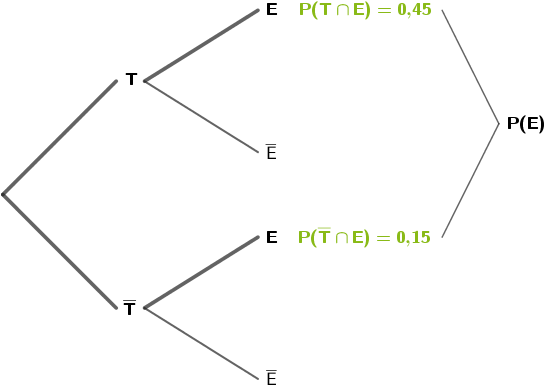
Die Berechnung der Wahrscheinlichkeit \(P(E)\) erfolgt mit der 2. Pfadregel.
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}P(E) &= \textcolor{#89ba17}{P(T \cap E)} + \textcolor{#89ba17}{P(\overline{T} \cap E)} \\[0.8em] &= 0{,}45 + 0{,}15 \\[0.8em] &= 0{,}6 \end{align*}\]
Ereignisse \(T\) und \(E\) auf stochstische Unabhängigkeit prüfen:
Stochastische (Un)Abhängigkeit von zwei Ereignissen
Zwei Ereignisse \(A\) und \(B\) heißen stochastisch unabhängig, wenn
\(P(A) \cdot P(B) = P(A \cap B)\) gilt. (vgl. Merkhilfe) *
Andernfalls heißen die Ereignisse \(A\) und \(B\) stochastisch abhängig.
Sind zwei Ereignisse \(A\) und \(B\) stochastisch unabhängig, beeinflusst das Eintreten des Ereignisses \(A\) nicht das Eintreten des Ereignisses \(B\) und umgekehrt.
* Oder wenn
\(P(\overline{A}) \cdot P(B) = P(\overline{A} \cap B)\) bzw.
\(P(A) \cdot P(\overline{B}) = P(A \cap \overline{B})\) bzw.
\(P(\overline{A}) \cdot P(\overline{B}) = P(\overline{A} \cap \overline{B})\) gilt.
\[P(T) \cdot P(E) = 0{,}6 \cdot 0{,}5 = 0{,}3 \textcolor{#cc071e}{\neq} 0{,}45 = P(T \cap E)\]
Die Ereignisse \(T\) und \(E\) sind stochastisch abhängig.


