Die Spitze einer Pyramide mit der Grundfläche \(IJKL\) liegt auf der Kante \([FG]\). Untersuchen Sie, ob die Höhe dieser Pyramide 2 betragen kann.
(4 BE)
Lösung zu Teilaufgabe f
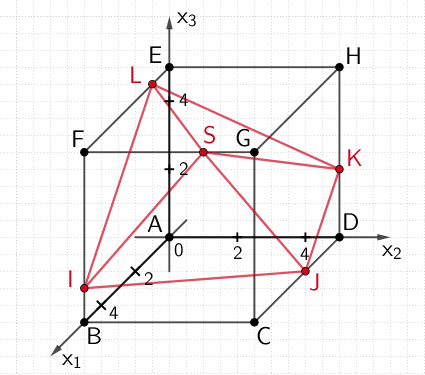
Die Spitze \(S\) der Pyramide \(IJKLS\) liegt auf der Strecke \([FG]\) und hat entsprechend der Abbildung die Koordinaten \(\textcolor{#cc071e}{S(5|s|5)}\) mit \(\textcolor{#cc071e}{s \in [0;5]}\).
Die Höhe einer Pyramide ist definiert als der Abstand der Pyramidenspitze von der Ebene in der die Grundfläche der Pyramide liegt.
Es ist also zu überprüfen, ob die Spitze \(S\) den Abstand \(d(S;T) = 2\) von der Ebene \(T\) haben kann, in der die Grundfläche \(IJKL\) der Pyramide \(IJKLS\) liegt.
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
Hessesche Normalenform der Ebene \(T\) bestimmen:
\(T \colon \textcolor{#0087c1}{5}x_{1} + \textcolor{#0087c1}{4}x_{2} + \textcolor{#0087c1}{5}x_{3} - 30 = 0\) (vgl. Teilaufgabe b)
\[\begin{align*}T_{HNF} \colon \frac{5x_{1} + 4x_{2} + 5x_{3} - 30}{\sqrt{\textcolor{#0087c1}{5}^{2} + \textcolor{#0087c1}{4}^{2} + \textcolor{#0087c1}{5}^{2}}} \\[0.8em] T_{HNF} \colon \frac{5x_{1} + 4x_{2} + 5x_{3} - 30}{\sqrt{66}} \end{align*}\]
Damit lässt sich der Abstand \(d(S;T)\) der Spitze \(S\) von der Ebene \(T\) wie folgt ermitteln:
\[S(5|s|5); \; s \in [0;5]\]
\[d(S;T) = \left| \frac{5 \cdot 5 + 4 \cdot s + 5 \cdot 5 - 30}{\sqrt{66}} \right| = \left| \frac{4s + 20}{\sqrt{66}} \right|\]
Mit \(s \in [0;5]\) folgt:
\[d(S;T) \geq \frac{20}{\sqrt{66}} > 2 \quad \left( \frac{20}{\sqrt{66}} \approx 2{,}46 \right)\]
Die Höhe der Pyramide \(IJKLS\) kann nicht 2 betragen.


