- Details
- Kategorie: Analysis 1
Gegeben ist die Funktion \(f \colon x \mapsto \sqrt{1 - \ln{x}}\) mit maximaler Definitionsmenge \(D\).
Bestimmen Sie \(D\).
(2 BE)
- Details
- Kategorie: Analysis 1
Zeigen Sie, dass der Graph der in \(\mathbb R\) definierten Funktion \(g \colon x \mapsto x^{2} \cdot \sin{x}\) punktsymmetrisch bezüglich des Koordinatenursprungs ist, und geben Sie den Wert des Integrals \(\displaystyle \int_{-\pi}^{\pi} x^{2} \cdot \sin{x}\, dx\) an.
(3 BE)
- Details
- Kategorie: Analysis 1
Skizzieren Sie im Bereich \(-1 \leq x \leq 4\) den Graphen einer in \(\mathbb R\) definierten Funktion \(f\) mit den folgenden Eigenschaften:
● \(f\) ist nur an der Stelle \(x = 3\) nicht differenzierbar.
● \(f(0)\) = 2 und für die Ableitung \(f'\) von \(f\) gilt: \(f'(0) = -1\).
● Der Graph von \(f\) ist im Bereich \(-1 < x < 3\) linksgekrümmt.
(3 BE)
- Details
- Kategorie: Analysis 1
Gegeben ist eine in \(\mathbb R\) definierte ganzrationale Funktion \(f\) dritten Grades, deren Graph \(G_{f}\) an der Stelle \(x = 1\) einen Hochpunkt und an der Stelle \(x = 4\) einen Tiefpunkt besitzt.
Begründen Sie, dass der Graph der Ableitungsfunktion \(f'\) von \(f\) eine Parabel ist, welche die \(x\)-Achse in den Punkten \((1|0)\) und \((4|0)\) schneidet und nach oben geöffnet ist.
(3 BE)
- Details
- Kategorie: Analysis 1
Begründen Sie, dass \(2{,}5\) die \(x\)-Koordinate des Wendepunkts von \(G_{f}\) ist.
(2 BE)
- Details
- Kategorie: Analysis 1
Die Abbildung zeigt den Graphen der in \(\mathbb R\) definierten Funktion \(f\).
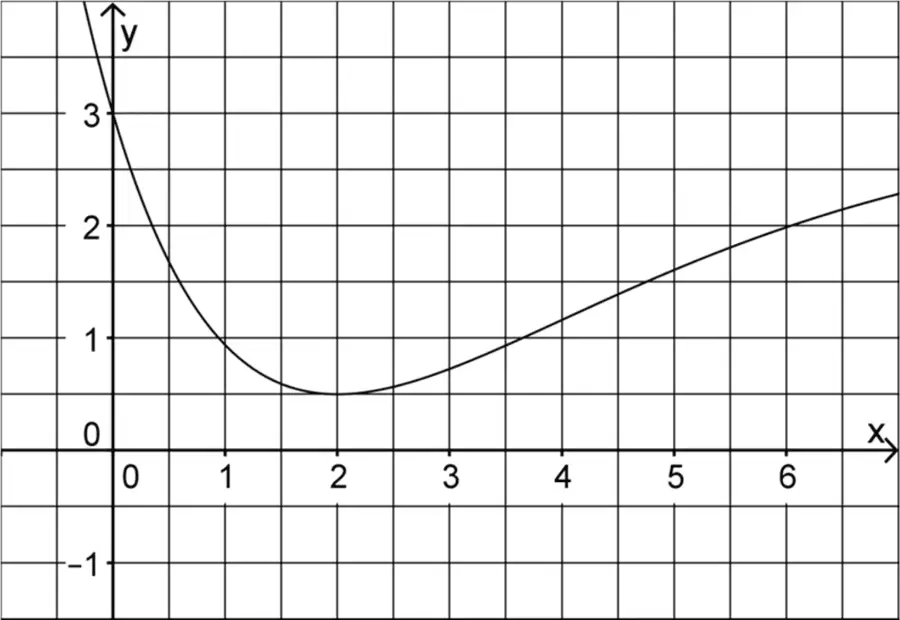
Bestimmen Sie mithilfe der Abbildung einen Näherungswert für \(\displaystyle \int_{3}^{5} f(x) \,dx\).
(2 BE)
- Details
- Kategorie: Analysis 1
Die Funktion \(F\) ist die in \(\mathbb R\) definierte Stammfunktion von \(f\) mit \(F(3) = 0\).
Geben Sie mithilfe der Abbildung einen Näherungswert für die Ableitung von \(F\) an der Stelle \(x = 2\) an.
(1 BE)
- Details
- Kategorie: Analysis 1
Zeigen Sie, dass \(\displaystyle F(b) = \int_{3}^{b} f(x) \, dx\) mit \(b \in \mathbb R\) gilt.
(2 BE)


