- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f\) mit \(f(x) = e^{2x + 1}\). Zeigen Sie, dass \(f\) umkehrbar ist, und ermitteln Sie einen Term der Umkehrfunktion von \(f\).
(4 BE)
- Details
- Kategorie: Analysis 1
Gegeben ist die Funktion \(g \colon x \mapsto (x^{2} - 9x) \cdot \sqrt{2 - x}\) mit maximaler Definitionsmenge \(D_{g}\). Geben Sie \(D_{g}\) und alle Nullstellen von \(g\) an.
(3 BE)
- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R\) definierte Funktion \(h \colon x \mapsto \ln{\left( \dfrac{1}{x^{2} + 1} \right)}\). Begründen Sie, dass die Wertemenge von \(h\) das Intervall \(]-\infty;0]\) ist.
(3 BE)
- Details
- Kategorie: Analysis 1
Betrachtet wird die in \(\mathbb R^{+}\) definierte Funktion \(f\) mit \(f(x) = \dfrac{1}{\sqrt{x^{3}}}\).
Zeigen Sie, dass die in \(\mathbb R^{+}\) definierte Funktion \(F\) mit \(F(x) = -\dfrac{2}{\sqrt{x}}\) eine Stammfunktion von \(f\) ist.
(2 BE)
- Details
- Kategorie: Analysis 1
Der Graph von \(f\) schließt mit der \(x\)-Achse sowie den Geraden mit den Gleichungen \(x = 1\) und \(x = b\) mit \(b > 1\) ein Flächenstück ein. Bestimmen Sie denjenigen Wert von \(b\), für den dieses Flächenstück den Inhalt 1 hat.
(3 BE)
- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f\) mit \(f(x) = \frac{1}{8}x^{3}\) sowie die Punkte \(Q_{a}(a|f(a))\) für \(a \in \mathbb R\). Die Abbildung zeigt den Graphen von \(f\) sowie die Punkte \(P(0|2)\) und \(Q_{2}\).
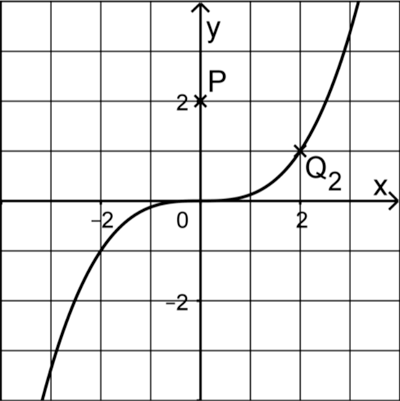
Berechnen Sie für \(a \neq 0\) die Steigung \(m_{a}\) der Gerade durch die Punkte \(P\) und \(Q_{a}\) in Abhängigkeit von \(a\).
(zur Kontrolle: \(m_{a} = \dfrac{a^{3} - 16}{8a}\))
(2 BE)
- Details
- Kategorie: Analysis 1
Die Tangente an den Graphen von \(f\) im Punkt \(Q_{a}\) wird mit \(t_{a}\) bezeichnet. Bestimmen Sie rechnerisch denjenigen Wert von \(a \in \mathbb R\), für den \(t_{a}\) durch \(P\) verläuft.
(3 BE)

