In einer Urne befinden sich eine gelbe und zwei blaue Kugeln. Es werden nacheinander drei Kugeln gezogen und deren Farbe notiert. Die gezogene Kugel wird jeweils zurückgelegt und zwei weitere Kugeln derselben Farbe in die Urne gegeben. Die Zufallsgröße \(X\) beschreibt die Anzahl der gezogenen gelben Kugeln.
a) Erstellen Sie ein vollständig beschriftetes Baumdiagramm und geben Sie den Ergebnisraum an.
b) Berechnen Sie die Wahrscheinlichkeit \(P(X \geq 1)\).
c) Beschreiben Sie im Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit sich mithilfe des Terms \(1 - P(X = 3)\) berechnen lässt.
a) Vollständig beschriftetes Baumdiagramm und Ergebnisraum
\(g\): „Eine gelbe Kugel wird gezogen."
\(b\): „Eine blaue Kugel wird gezogen."
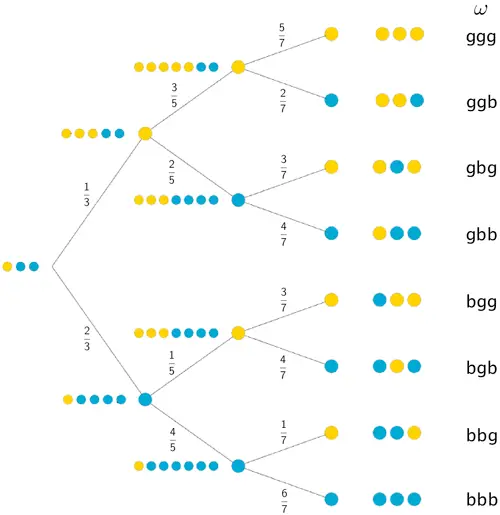
Baumdiagramm mit den Eintragungen der Wahrscheinlichkeiten an den Ästen der ersten, zweiten und dritten Stufe sowie allen Ergebnissen des Zufallsexperiments
An den Knotenpunkten ist der jeweilige Ist-Zustand der Urne veranschaulicht.
Erläuterung am Beispiel des Ergebnisses \(\{ggg\}\):
Zu Beginn befinden sich eine gelbe und zwei blaue Kugeln in der Urne. Die Wahrscheinlichkeit, eine gelbe Kugel zu ziehen beträgt \(\frac{1}{3}\). Nachdem eine gelbe Kugel gezogen und deren Farbe notiert wurde, wird diese in die Urne zurückgelegt und zwei weitere gelbe Kugeln in die Urne gegeben.
Es befinden sich nun drei gelbe und zwei blaue Kugeln in der Urne. Mit der Wahrscheinlichkeit \(\frac{3}{5}\) wird eine zweite gelbe Kugel gezogen, deren Farbe notiert und die gelbe Kugel wieder zurückgelegt. Wiederum werden zwei weitere gelbe Kugeln in die Urne gegeben.
Dann befinden sich fünf gelbe und zwei blaue Kugeln in der Urne. Die Wahrscheinlichkeit, eine dritte gelbe Kugel zu ziehen, beträgt schließlich \(\frac{5}{7}\).
Ergebnisraum \(\Omega\):
Die Menge aller Ergebnisse des Zufallsexperiments bildet den Ergebnisraum \(\Omega\), wobei jedes mögliche Ergebnis genau einmal in \(\Omega\) vorkommt (vgl. Abiturskript - 3.1.1 Ereignisse).
\[\Omega = \{ggg, ggb, gbg, gbb, bgg, bgb, bbg, bbb\}\]
b) Berechnung der Wahrscheinlichkeit \(P(X \geq 1)\)
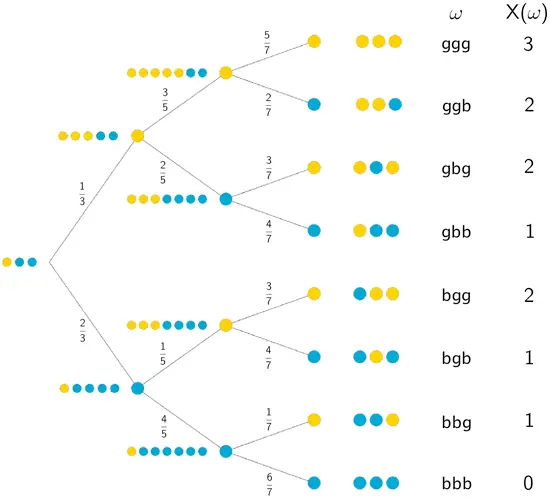
Die Zufallsgröße \(X\) beschreibt die Anzahl der gezogenen gelben Kugel und kann folglich die Werte \(x_{i} = \{0;1;2;3\}\) annehmen.
Die Wahrscheinlichkeit \(P(X \geq 1)\) bedeutet die Wahrscheinlichkeit für das Ereignis „Mindestens eine gelbe Kugel wird gezogen" und lässt sich günstiger mithilfe des Gegenereignisses „Keine gelbe Kugel wird gezogen" ausdrücken. Das Ereignis „Mindestens eine gelbe Kugel wird gezogen" ist gleichbedeutend mit dem Ereignis „Nicht keine gelbe Kugel wird gezogen".
Betrachten des Gegenereignisses
Wahrscheinlichkeitsberechnungen der Form "mindestens 1 Treffer" vereinfachen sich durch die Betrachtung des Gegenereignisses „nicht kein Treffer":
\[P(\text{"mindestens 1 Treffer"}) = 1 - P(\text{"kein Treffer"})\]
\[P(X \geq 1) = 1 - P(X = 0)\]
Die Wahrscheinlichkeit \(P(X = 0)\) lässt sich mithilfe der ersten Pfadregel berechnen.
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}P(X \geq 1) &= 1 - P(X = 0) \\[0.8em] &= 1 - \underbrace{\frac{2}{3} \cdot \frac{4}{5} \cdot \frac{6}{7}}_{\large{\text{1. Pfadregel}}} \\[0.8em] &= 1 - \frac{16}{35} \\[0.8em] &= \frac{19}{35} \\[0.8em] &\approx 0{,}543 \end{align*}\]
c) Beschreibung eines Ereignisses im Sachzusammenhang, dessen Wahrscheinlichkeit sich mithilfe des Terms \(1 - P(X = 3)\) berechnen lässt
Der Term \(P(X = 3)\) beschreibt die Wahrscheinlichkeit für das Ereignis „Drei gelbe Kugeln werden gezogen".
Dann beschreibt der Term \(1 - P(X = 3)\) die Wahrscheinlichkeit für das Ereignis „Es werden nicht drei gelbe Kugeln gezogen", was gleichbedeutend ist mit dem Ereignis „Mindestens ein blaue Kugel wird gezogen".

