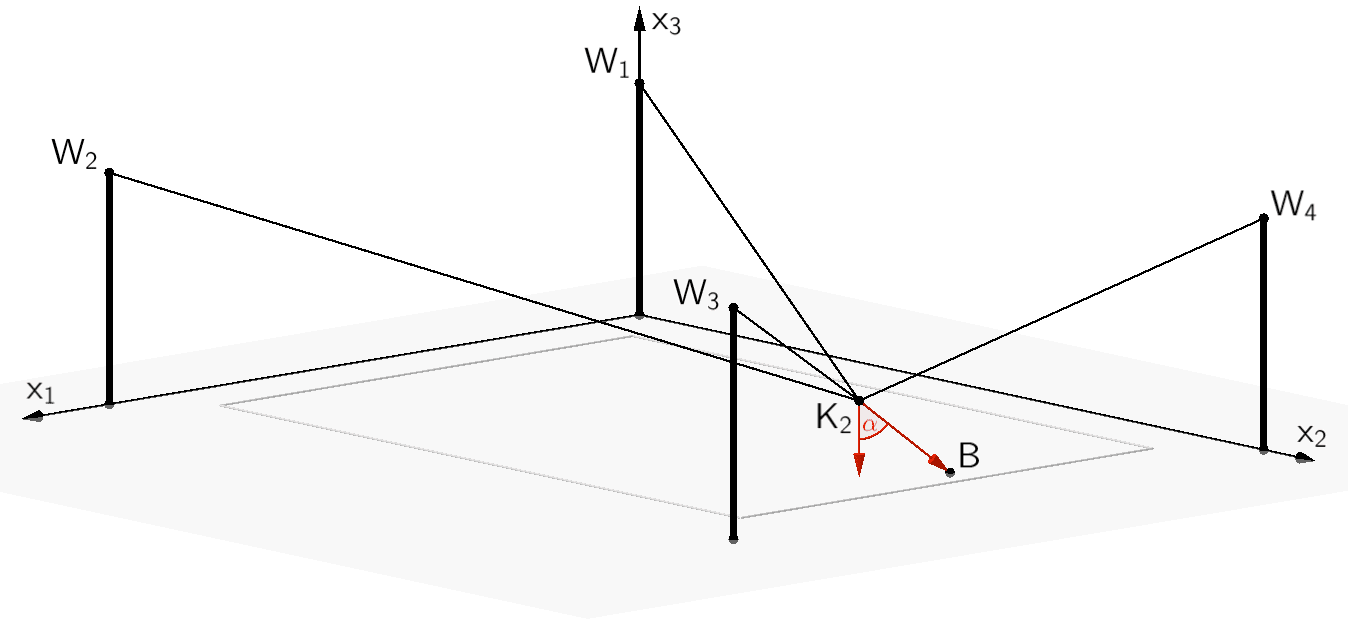
Im Zielpunkt ist die Kamera zunächst senkrecht nach unten orientiert. Um die Position des Balls anzuvisieren, die im Modell durch den Punkt \(B(40|105|0)\) beschrieben wird, muss die Kamera gedreht werden.
Berechnen Sie die Größe des erforderlichen Drehwinkels.
(4 BE)
Lösung zu Teilaufgabe c
Winkel zwischen zwei Vektoren
Spielfeld mit Position \(K_{2}\) der Kamera und Position \(B\) des Balls sowie Drehwinkel der Kamera
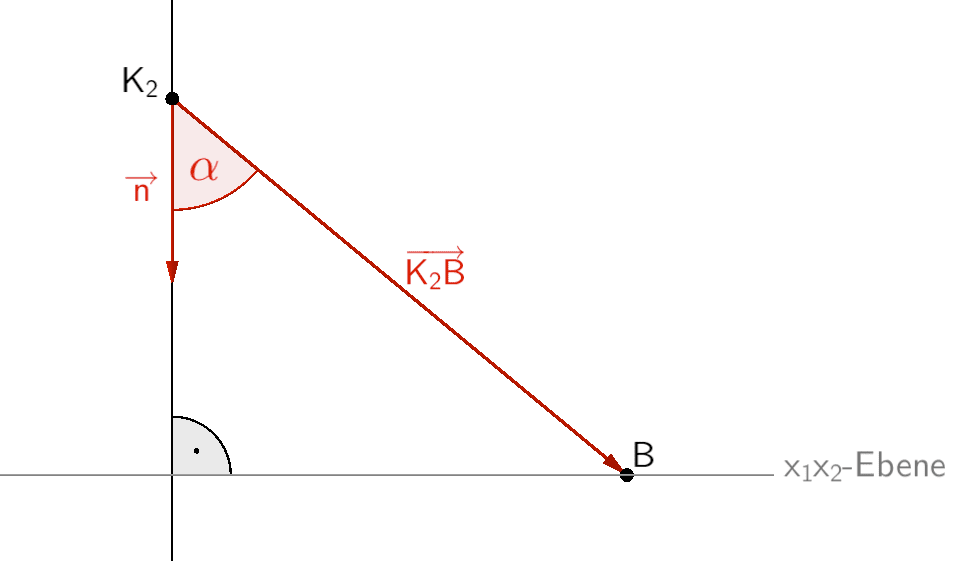
Der Drehwinkel der Kamera entspricht dem Winkel zwischen dem Verbindungsvektor \(\overrightarrow{K_{2}B}\) und einem Normalenvektor \(\overrightarrow{n}\) der \(x_{1}x_{2}\)-Ebene, welcher die ursprünglich senkrecht nach unten orientierte Kamera repräsentiert.
Anwendung des Skalarprodukts:
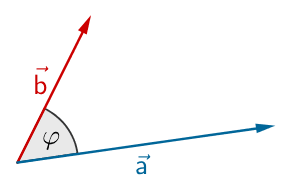
Winkel zwischen zwei Vektoren (vgl. Merkhilfe)
\[\cos \varphi = \frac{\overrightarrow{a} \circ \overrightarrow{b}}{\vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert}\,; \quad \varphi \in [0;\pi]\]
Normalenvektor \(\overrightarrow{n}\) der \(x_{1}x_{2}\)-Ebene festlegen:
Ein geeigneter Normalenvektor, der die senkrecht nach unten orientierte Kamera beschreibt, ist beispielsweise der Normalenvektor \(\overrightarrow{n} = \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix}\).
Verbindungsvektor \(\overrightarrow{K_{2}B}\) bestimmen:
\(B(40|105|0)\), \(K_{2}(51|100|10)\) (vgl. Teilaufgabe b)
\[\overrightarrow{K_{2}B} = \overrightarrow{B} - \overrightarrow{K_{2}} = \begin{pmatrix} 40 \\ 105 \\ 0 \end{pmatrix} - \begin{pmatrix} 51 \\ 100 \\ 10 \end{pmatrix} = \begin{pmatrix} -11 \\ 5 \\ -10 \end{pmatrix}\]
Winkel \(\alpha\) zwischen den Vektoren \(\overrightarrow{K_{2}B}\) und \(\overrightarrow{n}\) berechnen:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \cos \alpha &= \frac{\overrightarrow{K_{2}B} \circ \overrightarrow{n}}{\Big| \overrightarrow{K_{2}B} \Big| \cdot \left| \overrightarrow{n} \right|} \\[0.8em] &= \frac{\begin{pmatrix} -11 \\ 5 \\ -10 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix}}{\left| \begin{pmatrix} -11 \\ 5 \\ -10 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} \right|} \\[0.8em] &= \frac{(-11) \cdot 0 + 5 \cdot 0 + (-10) \cdot (-1)}{\sqrt{(-11)^{2} + 5^{2} + (-10)^{2}} \cdot \sqrt{0^{2} + 0^{2} (-1)^{2}}} \\[0.8em] &= \frac{10}{\sqrt{246}} & &| \; \text{TR:} \; \cos^{-1}(\dots) \\[3.2em] \alpha &\approx 50{,}39^{\circ} \end{align*}\]
Um die Position des Balls anzuvisieren, muss die Kamera um ca. 50,39° gedreht werden.