- Details
- Kategorie: Geometrie 1
Betrachtet wird der abgebildete Würfel \(ABCDEFGH\).
Die Eckpunkte \(D\), \(E\), \(F\) und \(H\) dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten: \(D(0|0|-2)\), \(E(2|0|0)\), F(2|2|0) und \(H(0|0|0)\).
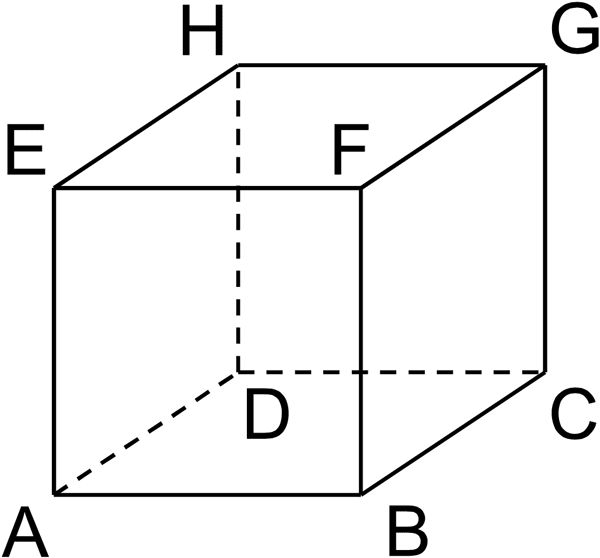
Zeichnen Sie in die Abbildung die Koordinatenachsen ein und bezeichnen Sie diese. Geben Sie die Koordinaten des Punkts \(A\) an.
(2 BE)
- Details
- Kategorie: Geometrie 1
Der Punkt \(P\) liegt auf der Kante \([FB]\) des Würfels und hat vom Punkt \(H\) den Abstand 3. Berechnen Sie die Koordinaten des Punkts \(P\).
(3 BE)
- Details
- Kategorie: Geometrie 1
Gegeben sind die Punkte \(A(-2|1|4)\) und \(B(-4|0|6)\)
Bestimmen Sie die Koordinaten des Punkts \(C\) so, dass gilt: \(\overrightarrow{CA} = 2 \cdot \overrightarrow{AB}\).
(2 BE)
- Details
- Kategorie: Geometrie 1
Durch die Punkte \(A\) und \(B\) verläuft die Gerade \(g\).
Betrachtet werden Geraden, für welche die Bedingungen I und II gelten:
I Jede dieser Geraden schneidet die Gerade \(g\) orhogonal.
II Der Abstand jeder dieser Geraden vom Punkt \(A\) beträgt 3.
Ermitteln Sie eine Gleichung für eine dieser Geraden.
(3 BE)


